Funkcje kwadratowe - równania kwadratowe, postać kanoniczna i iloczynowa.

1. Zapisz ogólną postać równania kwadratowego i wyjaśnij znaczenie symboli: a, b, c, x.

2. Zapisz postać kanoniczną trójmianu kwadratowego i wyjaśnij znaczenie symboli a, p i q.

3. Jak sprawdzić, czy dana liczba jest rozwiązaniem (pierwiastkiem) równania? Sprawdź, która z liczb: 0, 1, -1, 2,
   ,
   ,
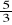
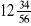
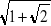
   jest pierwiastkiem równania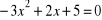
   .

4. Sprowadź do postaci kanonicznej następujące funkcje. Narysuj ich wykresy (po 4 na jednym układzie współrzędnych). Jakie widzisz między nimi różnice? Jaka jest zależność między odciętą wierzchołka p, a miejscami zerowymi funkcji?
   a)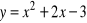
   ,
   ,
   ,
   ,

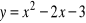
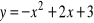
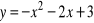
b)
,
,
,
.

Przykład: Funkcję
przekształć do postaci iloczynowej.

I sposób (gorszy):
, zatem
, czyli
.

II sposób (lepszy):
. Skorzystałem ze wzoru skr. mnożenia (którego?)

5. Funkcję podaną w postaci kanonicznej przekształć do postaci ogólnej, a następnie (jeśli można!) do postaci iloczynowej

a)
, b)
, c)
, d)
, e)
.

Przykład: Funkcję
przekształć do postaci kanonicznej, podaj współrzędne wierzchołka:

I sposób (gorszy): wymnażamy do postaci ogólnej:
. Mamy
.
Obliczamy teraz p i q ze znanych wzorów:
i gotowe:
.

II sposób (ciekawszy):
,
. Skoro wierzchołek jest „w środku” między miejscami zerowymi, to
, a q to przecież wartość tej funkcji dla
(!!!) zatem
, i gotowe:
.

6. Funkcję w postaci iloczynowej przekształć do postaci kanonicznej (jedną - wszystko mi jedno którą - z powyższych metod):

a)
,

b)
,

c)
,

d)
,

e)
,

f)
.

8. Jak rozwiązuje się równania niezupełne, w których współczynnik c jest równy zero (
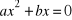
   )? Jaka liczba zawsze będzie rozwiązaniem takiego równania (poszperaj w książce i przejrzyj przykłady z zeszytu...)?

9. Rozwiąż równania niezupełne:

a)
,

b)
,

c)
,

d)
,

e)
,

f)
,

g)
,

h)
,

i)

j)
.
k)

l)

11. Jak rozwiązuje się równania niezupełne, w których współczynnik b jest równy zero (
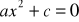
    )? Czy takie równanie zawsze ma rozwiązanie?

12. Rozwiąż równania niezupełne:

a)
,

b)
,

c)
,

d)
,

e)
,

f)
,

g)
,

h)
,

i)
,

j)
.

k)
,

l)
.

15. Jak rozwiązuje się równania zupełne? Ile rozwiązań ma równanie kwadratowe, jeśli: a)
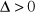
    , b)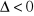
    , c)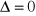
    ?

16. Rozwiąż następujące równania zupełne ( najpierw przenieś wszystko na lewą stronę ):
    a)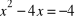
    , b)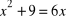
    , c)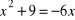
    , d)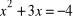
    , e)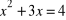
    .

17. Rozwiąż równanie zupełne:
    

a)
,
b)
,
c)
, d)
,
e)
,
f)
.

g)
,

h)
,

i)
=0,

j)
,

k)
, l) 
.

18. Trójmiany z lewych stron równań z poprzedniego zadania, sprowadź, jeśli można, do postaci iloczynowej.

19. Trójmiany z lewych stron równań z zadania 13 sprowadź do postaci kanonicznej. Obok podaj współrzędne wierzchołka paraboli.

Przykład: Napiszemy ogólne równanie funkcji, której miejscami zerowymi są liczby 2 i -5 i której wykres przechodzi przez punkt (1,6). Ta funkcja ma postać
i jednocześnie
. zatem
, więc
.

20. Napisz równanie ogólne funkcji, której miejscami zerowymi są liczby -1 i 2 i której wykres przechodzi przez punkt (0,4).

21. Napisz równanie ogólne funkcji, której miejscami zerowymi są liczby
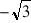
    i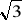
    i której wykres przechodzi przez punkt (2,-2).

---