FUNKCJE
1. Podstawowe określenia
(1.1) Definicja
Funkcją określoną na zbiorze 
o wartościach w zbiorze 
nazywamy przyporządkowanie każdemu elementowi 
dokładnie jednego elementu 
. Funkcję taką oznaczamy np.:
Wartość funkcji f w punkcie x oznaczamy przez f(x).
(1.2) Definicja
Niech 
. Wtedy zbiór X nazywamy dziedziną funkcji f i oznaczamy przez 
, a zbiór 
nazywamy jej przeciwdziedziną. Ponadto zbiór 
nazywamy zbiorem wartości funkcji f i oznaczamy 
.
Uwaga. Rzut prostokątny wykresu funkcji na oś Ox jest dziedziną tej funkcji, zaś rzut prostokątny tego wykresu na oś Oy jest zbiorem jej wartości.
(1.3) Definicja
Funkcje 
są równe, co zapisujemy
.
(1.4) Definicja
Wykresem funkcji 
nazywamy zbiór 
.
Uwaga. Podzbiór płaszczyzny xOy jest wykresem pewnej funkcji zmiennej x, gdy każda prosta pionowa przecina go co najwyżej w jednym punkcie.
(1.5) Definicja (funkcja "na")
Funkcja f odwzorowuje zbiór X na zbiór Y, (co zapisujemy 
)
, tzn. 
.
Geometrycznie: funkcja 
jest "na", gdy rzut prostokątny jej wykresu
na oś Oy pokrywa się ze zbiorem Y.
2. Funkcje okresowe, parzyste i nieparzyste, ograniczone,
monotoniczne
(2.1) Definicja
Funkcja 
jest okresowa, jeżeli
Literę T nazywamy okresem funkcji f. Jeżeli istnieje najmniejszy okres funkcji f, to nazywamy go jej okresem podstawowym.
(2.2) Definicja
Funkcja 
jest parzysta, jeżeli
Obrazowo: funkcja jest parzysta, gdy oś Oy jest osią symetrii jej wykresu.
(2.3) Definicja
Funkcja 
jest nieparzysta, jeżeli
Obrazowo: funkcja jest nieparzysta, gdy początek układu współrzędnych jest środkiem symetrii jej wykresu.
(2.4) Definicja
Funkcja 
jest ograniczona z dołu na zbiorze 
, jeżeli zbiór jej wartości na tym zbiorze jest ograniczony z dołu, tzn. 
(2.5) Definicja
Funkcja 
jest ograniczona z góry na zbiorze 
, jeżeli zbiór jej wartości na tym zbiorze jest ograniczony z góry, tzn. 
(2.6) Definicja
Funkcja 
jest ograniczona na zbiorze 
, jeżeli jest ograniczona z dołu i z góry na tym zbiorze, tzn. 
(2.7) Definicja
Funkcja f jest rosnąca (niemalejąca) na zbiorze 
, jeżeli
.
.
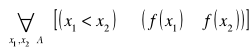
(2.8) Definicja
Funkcja f jest malejąca (nierosnąca) na zbiorze 
, jeżeli
.
.
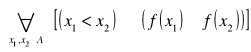
(2.9) Definicja
Funkcja jest monotoniczna na zbiorze, jeżeli jest rosnąca, malejąca, nierosnąca lub niemalejąca w tym zbiorze. Przy czym funkcje rosnące i malejące nazywamy ściśle monotonicznymi, a funkcje nierosnące i niemalejące - słabo monotonicznymi.
3. Złożenia funkcji (superpozycja funkcji)
(3.1) Definicja
Niech X, Y, Z, W będą podzbiorami zbioru liczb rzeczywistych, przy czym 
oraz niech 
, 
. Złożeniem funkcji g i f nazywamy funkcję 
określoną wzorem:
przy czym, funkcję f nazywamy funkcją wewnętrzną, a g - funkcją zewnętrzną funkcji 
.
Złożenie dwóch funkcji jest możliwe, gdy przeciwdziedzina funkcji wewnętrznej * dziedzinie funkcji zewnętrznej.
Uwaga. Analogicznie określa się złożenie większej liczby funkcji. Składanie funkcji nie jest przemienne.
(3.1) Fakt (o składaniu funkcji monotonicznych)
Złożenie funkcji ściśle rosnących (malejących) jest funkcją rosnącą.
Złożenie funkcji ściśle rosnącej (malejącej) z funkcją ściśle malejącą (rosnącą) jest funkcją malejącą. Złożenie funkcji ciągłych jest funkcją ciągłą.
4. Funkcje odwrotne
(4.1) Definicja
Funkcja f jest różnowartościowa na zbiorze 
, jeżeli:
.
Uwaga. Przy sprawdzaniu różnowartościowości funkcji wygodnie jest korzystać
z definicji równoważnej:
.
(4.2) Fakt (warunek wystarczający różnowartościowości funkcji)
Jeżeli funkcja jest rosnąca albo malejąca na danym zbiorze, to jest w tym zbiorze różnowartościowa.
Uwaga. Implikacja odwrotna nie jest prawdziwa.
(4.3) Definicja
Niech 
będzie różnowartościowa na dziedzinie X. Funkcją odwrotną do f nazywamy funkcję 
określoną przez warunek:
gdzie 
.
Uwaga. Wykres funkcji odwrotnej 
otrzymujemy z wykresu funkcji
odbijając go symetrycznie względem prostej y = x.
(4.4) Fakt (o składaniu funkcji prostej i odwrotnej)
Niech funkcja 
będzie różnowartościowa. Wtedy
oraz 
.
5. Funkcje cyklometryczne (kołowe)
(5.1) Definicja
Funkcją arkus sinus nazywamy funkcję 
odwrotną do funkcji sinus obciętej do przedziału 
.
.
Funkcją arkus cosinus nazywamy funkcję 
odwrotną do funkcji cosinus obciętej do przedziału 
.
.
Funkcją arkus tangens nazywamy funkcję 
odwrotną do funkcji tangens obciętej do przedziału
.
.
Funkcją arkus kotangens nazywamy funkcję 
odwrotną do funkcji kotangens obciętej do przedziału
.
.
6. Inne rodzaje funkcji
(6.1) Definicja
Wartością bezwzględną nazywamy funkcję
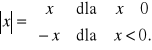
(6.2) Definicja (funkcje hiperboliczne)
Funkcję sh (sinus hiperboliczny) określamy wzorem:
, gdzie 
.
Funkcję ch (cosinus hiperboliczny) określamy wzorem:
, gdzie 
.
Funkcję th (tangens hiperboliczny) określamy wzorem:
, gdzie 
.
Funkcję cth (cotangens hiperboliczny) określamy wzorem:
, gdzie 
.
(6.3) Definicja
Funkcją część całkowita nazywamy funkcję 
określoną wzorem
(
, gdzie 
).
Część całkowita liczby x jest to największa liczba całkowita nie większą niż x.
(6.4) Definicja
Funkcją signum nazywamy funkcję 
określoną wzorem:
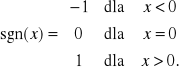
(6.5) Definicja
Funkcją Dirichleta nazywamy funkcję 
określoną wzorem:
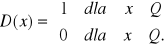
(6.6) Definicja (funkcja Riemanna)
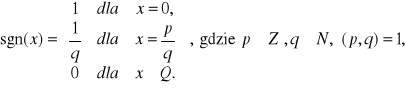
5
Wyszukiwarka