Literatura:

1. „Prognozowanie gospodarcze” M Cieślak, PWN III wydanie

2. „Prognozowanie gospodarcze” Dittman AE Wrocław

3. „Predykcja ekonometryczna” A. Zewiasz

Wykład 1 - 13.10.2001

Wyznaczanie prognoz

Prognozowanie ilościowe czyli predykcja pozwala wyznaczać prognozy za pomocą przesłanek z modeli ekonometrycznych. Nie dotyczy ono tylko przyszłości ale może także dotyczyć przeszłości lub teraźniejszości. Prognozowanie ma ścisłe powiązania z demografią.

Prognozowanie wykorzystywane jest między innymi w Głównym Urzędzie Statystycznym oraz w dużych przedsiębiorstwach czy centralach gdzie za pomocą prognozowania ocenia się perspektywy planowanej produkcji.

Podstawowe pojęcia:

model ekonometryczny

(wg Z. Czerwińskiego) - może być rozumiany ogólnie, intuicyjnie jako obraz, odbicie, odwzorowanie określonego obiektu w określonym języku.

Model ekonometryczny - również będzie układem równań odwzorowującym wyróżnione zależności między zjawiskami ekonomiczno - społecznymi.

Część związków można mierzyć a niektóre nie.

Związki mierzalne nazywane są korelacyjnymi.

Y = f (x₁, x₂ ......x_kၖ)

y - zjawisko badane

x₁,x₂-zjawiska, czynniki

ၖ- składnik losowy (psi,) - jest to łączny efekt oddziaływania na zmienną y, oddziałuje na te i inne czynniki, które nie zostały uwzględnione bezpośrednio w zbiorze x.

Jest to zmienna losowa o określonym rozkładzie.

E(ၖ) = 0; D²(ၖ) = ၤ² = const. (ၤ² - wariancja)

liniowy model ekonometryczny

Y_t = ၡ₀ + ၡ₁x_t + ၸ_t t = 1,2,………….,n

gdzie:

ၸ_t - składnik losowy

ၡ₀ - współczynnik kierunkowy funkcji regresji

Aby przedłużyć prognozę od 1,2,.............,n należy wykonać estymację parametrów ၡ₀ i ၡ₁.

Do estymacji parametrów wykorzystuje się metodę najmniejszych kwadratów.

MNK polega na znajdowaniu takich wartości ocen parametrów strukturalnych modelu, by suma kwadratów odchyleń zaobserwowanych (empirycznych) wartości i zmiennej y, od jej wartości teoretycznych wyznaczonych przez model była najmniejsza w przypadku jednej zmiennej objaśniającej.

MNK polega na znajdowaniu takiej prostej , która jest najlepiej dopasowana, do wszystkich punktów empirycznych, czyli minimalizowana jest sumą kwadratów reszt (u_t).

Klasyczne założenia MNK

1. Zmienne objaśniające x są nielosowe i niewspółliniowe k<n;

2. Istnieje n populacji składników losowych, o nadziejach matematycznych E(ၖ_t)=0 i stałych wariancjach o skończonych wartościach ၤ² =D²(ၖ_t) = const, t= 1, 2, 3, ...... n.

3. Realizacje zmiennych tworzą proces czysto losowy tzn., że następuje po sobie realizacja składnika losowego , są nieskorelowane, czyli ρ(ၖ_t; ၖ_ts)= 0 dla t ≠ s

4. składniki losowe są nieskorelowane ze zmiennymi objaśniajacymi.

Jeżeli ww. założenia są spełnione to estymator ma dobre własności tzn.

jest nieobciążony;

zgodny;

najbardziej efektywny;

f (₀, ₁) =
(Y_t - ₀ - ₁x_t)² =
e_t²

e_t² = Y_t - (₀ - ₁x_t)

^ ^

f (₀, ₁) = minimum

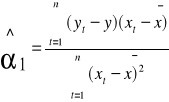
gdy wartość zmiennej objaśniającej zależy od więcej niż jednej zmiennej objaśnianej

Y_t = ၡ₀ + ၡ₁x_t1 + ၡ₂x_t2 + …………. + ၡ_kx_tk + ၸ_t

t = 1,2,……………,n

parametr „ၡ₁” wskazuje o ile przeciętnie zmieni się wartość „y” jeśli „x₁” zmieni się o jedną jednostkę w pewnym okresie czasu.

szeregi czasowe - są realizacją procesu stochastycznego który możemy zapisać ciągiem zmiennych losowych.

ၻy_tၽ= ၻy_1, y₂, ................., y_nၽ szeregi czasowe

gdy „t” jest okresem miesiąca to:

„y₁” to np. styczeń

_„y₂” to luty itd.

gdy zaobserwujemy już jakiś proces wówczas oznaczamy dane małymi literami.

momenty czasu

ၻY_tၽ= ၻY_1, Y₂, ................., Y_nၽ

zmienna “Y” jest pewną funkcją która może

przybierać różne wartości „y”

0,3 dla y = 0

PၻY=yၽ = 0,5 dla y = 1

0,2 dla y = 2

PၻY=yၽ = 0 < p < 1

realizacja procesu to ciąg: ၻ0,0,1,1,0,0,0,1ၽ

^

oceniając p wyznaczamy prognozę

„p” zmienia się jednak z czasem

P ၻY_t=yၽ = 0 < p < 1

Rachunek macierzowy

Y =
x =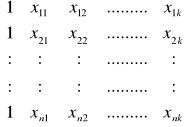

n x 1 n x (k+1)

Składnik losowy - ၸ (ksi)

ၸ =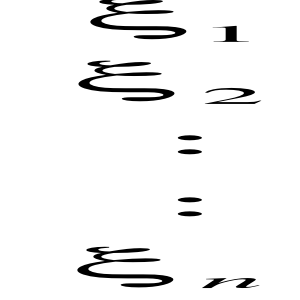
ၡ =

n x 1 (k + 1) x 1

f (α₀, α_{1, ...................} α_k) =

lub w formie macierzowej:

Y = Xα + ξ Y_* = Xα ; Y_* - wartość teoretyczna funkcji regresji

f(α) = (Y - Y_t)^T(Y - Y_*) = (Y - X_d)^T(Y - X_α)

gdy, chcemy obliczyć średni błąd szacunku stawiamy hipotezę, że α₀ = 0 i próbujemy ją zweryfikować.

Główne klasyczne założenia regresji liniowej.

1. zakładamy, że dla każdego „t” nadzieja matematyczna równa się 0.

2. zakładamy, że dla każdego „t” wariancja składnika losowego jest równa δ² - jest stała

składnik losowy ma rozkład homostechastyczny

3. gdy w czasie są nieskorelowane macierze składników losowych

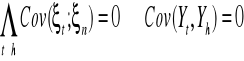
4. zakładamy, że wartości zmiennych objaśniających są nie losowe to znaczy są

ustalone z góry.

R(X) = k+1 ⇒ det (X^TX) > 0 R(X) - rząd macierzy

5. czasami wprowadzamy założenie, że wektor składników losowych ma

n-wymiarowy rozkład normalny z nadzieją matematyczną równą 0.

ξ ∼ N(0, I_n δ²) ⇒ Y ∼ N(Xα_i, I_n δ²)

wektor wartości funkcji regresji (wartości teoretyczne funkcji regresji)

wariancja resztowa

współczynnik zbieżności

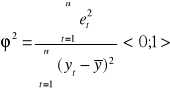
Macierz wariancji i dewariancji estymatorów.

D²(α) = (X^TX)^-1δ² S_e² ⇒ δ²

;

Hipotezy:

a) H₀ α_j = 0

b) H₁ α_j ≠ 0

j-oty parametr funkcji jest równy 0, nie ma wpływu ma zmienną objaśniającą.

Sprawdzian testu Studenta

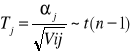
⁰

a → t_a → K = (-∞; -t_a > ∪ < t_a; ∞)

za „a” przyjmujemy małą liczbę np. 0,01; 0,05

Poziom istotności:

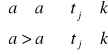
prognoza czy wartość symulowana

X_T - wartości hipotetyczne

Wykład 2 - 28.10.2001

Model potęgowy

t = 1,2, ........., n

najczęściej rozważany natomiast jest model:

gdzie:

Z_t - poziom zatrudnienia,

W_t - poziom środków trwałych,

α₁- elastyczność produkcji względem zatrudnienia.

model ten jest modelem nieliniowym

- estymacja modelu:

- logarytm modelu:

U_t, R_t, V_t - są nowymi zmiennymi

po obliczeniu otrzymujemy:

natomiast
]

Szczególne modele regresji (trendy).

a) model addytywny jest jednym z modeli szeregu czasowego

Y_t,h = f(t) + a(h) + ξ_t

trend wahania wahania

sezonowe losowe

trend f(t) jest funkcją kolejnych numerów czasów (generalnie obrazuje przyrost).

b) model multiplikatywny.

rozwój zjawiska obrazuje trend ale wahania sezonowe są coraz większe (brak stabilności)

Najprostszą formą trendu jest funkcja liniowa:

f₁(t) = β₀ + tβ₁ + ξ_t

Wyliczenie parametrów na podstawie wzorów analitycznych:

wzór 1:

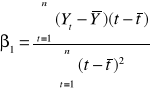
wzór 2:

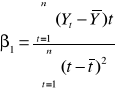
wzór 3:

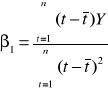
wzór na β₀:

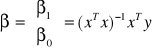
Zadanie:

W miesiącach od stycznia do kwietnia zaobserwowano następujące wydatki: 4, 6, 10, 8.

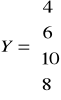
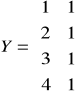
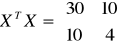
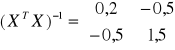
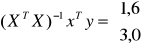
Interpretacja wyniku: Średnio z miesiąca na miesiąc wartość wydatków rosła o 1,6 jednostki.

t		Yt	Yt-
1	4,6	4	-0,6	0,36
2	6,2	6	-0,2	0,04
3	7,8	10	2,2	4,84
4	9,4	8	-1,4	1,96
Σ			0,0	7,2

suma reszt

jest to pośredni test sprawdzający poprawność wykonania zadania, gdy otrzymamy 0 zadanie uważa się za wykonane poprawnie.

obliczamy odchylenia wydatków od trendu:

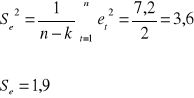
Interpretacja wyniku: Wydatki rzeczywiste odchylają się od trendu o 1,9 jednostki.

oceniamy błąd obliczeń:

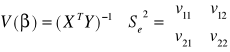
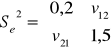
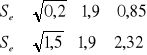
Interpretacja wyniku: Średni błąd szacunku czyli odchylenie standardowe estymatora pierwszego β₁ jest równe 0,85 jednostki (wskazuje to rząd błędu jakim szacowany jest parametr)

oceniamy względny błąd szacunku (błąd średni)

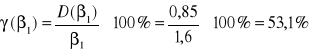
Interpretacja wyniku: Względny błąd szacunku stanowi 53,1% oceny całego szacunku.

Wyznaczamy prognozę na podstawie trendu:

Interpretacja wyniku: Prognoza równa jest 11 jednostek.

Obliczamy możliwy błąd prognozy:

czyli:
- średni błąd prognozowania czyli predykcji.

Interpretacja wyniku: Rzeczywiste prognozowania które występują w przyszłości mogą się odchylać o 5,2 jednostki.

Obliczamy odchylenie średniego błędu predykcji:

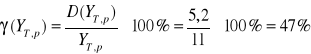
Rodzaje trendów liniowych.

a)

przyrost trendu liniowego

b) aby opisać krzywą z wykresu należy:

funkcja trendu zapisana jest w postaci funkcji regresji, do obliczenia jej używamy wzorów macierzowych.

c) krzywą tą możemy również modelować za pomocą funkcji wykładniczej:

i wyznaczamy logarytm:

;

d) inna postać trendu to:

model szeregu czasowego wygląda wtedy następująco:

i wyznaczamy logarytm:

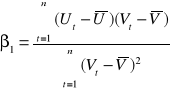
e) funkcja logarytmiczna:

f) funkcja logistyczna:

f(t) punkt nasycenia rynku

t

Zadanie:

Rozważamy wahania sezonowe o cyklu rocznym, obserwowane będą wartości cechy w poszczególnych miesiącach:

gdzie: t = 1,2 - bieżący numer miesiąca

h = 1,2,3,.......,12- miesiąc w cyklu wahań

k = 1,2,.... - numer roku .

np. obserwacja z piątego roku z marca

to: k=5; h=3

t = (5-1) x 12 + 3 = 48+3 = 51

z obliczenia wynika, że jest to 51 miesiąc z kolei w cyklu który obserwujemy.

cykl dwuokresowy:

określa amplitudę

wahania sezonowego

gdzie:

„t” - przyjmujemy jako bieżące półrocze

„h” - numer półrocza (0 - pierwsze półrocze, 1 - drugie półrocze)

„k” - numer roku

macierz danych przyjmuje następującą postać:

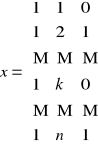
cykl kwartalny - wprowadzamy dwie zmienne zero - jedynkowe.

suma dwóch zmiennych

zero jedynkowych

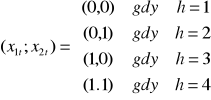
aby obliczyć cykl miesięczny musimy wprowadzić cztery zmienne zero jedynkowe

numer bieżący miesiąca:

t = (k-1)c+h

wahania sezonowe wprowadzają składnik losowy η_t (eta).

m - liczba wszystkich lat

np.

gdzie: t - numer bieżący kwartału

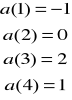
prognozy kwartalne

wyznacz prognozę na trzeci kwartał piątego roku:

k=5, H=3

T = (k-1)c+H

T = (5-1) 4+3 = 19

badany kwartał jest 19 z kolei badanym kwartałem

obliczamy prognozę:

Wykład 3 - 10.11.2001

Wyznaczanie tendencji rozwojowych zwanych trendami.

Metody adaptacyjne:

a) metoda średnich ruchomych - metoda wygładzania średnich czasowych.

t	Yt	(3)	(5)	(2)
1	2	-	-	-
2	4	3,3	-	3,5
3	4	5,3	4,0	5,0
4	8	4,7	4,8	5,5
5	2	5,3	4,4	4,5
6	6	3,3	4,4	4,0
7	2	4	-	3,5
8	4	-	-	-

obliczeń w tabeli dla średniej ruchomej scentrowanej trzyokresowej dokonano z wzoru:

a dla średniej ruchomej scentrowanej pięciookresowej z wzoru:

wykres szeregu
(3) oraz
(5) przedstawia się w sposób następujący:

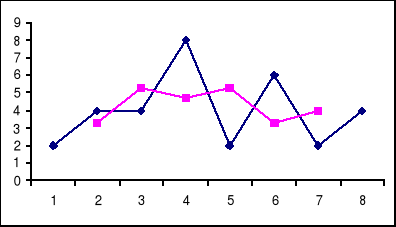
Im więcej składowych tym przebieg jest bardziej łagodny. Zazwyczaj rozważamy średnie 5, 10, 30 i 100 okresowe.

Uogólnienie wzoru na dowolną liczbę składników:

• gdy k jest liczbą nieparzystą:

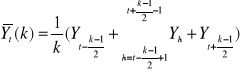
• gdy k jest liczbą parzystą:

dla k = 2

dla k = 4

dla dowolnej liczby parzystej:

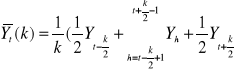
b) średnie ruchome uprzednie:

wzór ogólny:

w szczególności:

Im większe „k” tym prognoza wyznaczona na podstawie tendencji długookresowej a im mniejsze „k” prognoza zależna od czynników bieżących.

przykład:

t	Yt			Ut(2)	Ut(4)	Ut^2(2)	Ut^2(4)
1	2	-	-	-	-	-	-
2	4	-	-	-	-	-	-
3	4	3	-	1	-	1	-
4	8	4	-	4	-	16	-
5	2	6	4,5	- 4	-2,5	16	6,25
6	6	5	4,5	1	-1,5	1	2,25
7	2	4	5,0	- 2	-3,0	4	9
8	4	4	4,5	0	-0,5	0	0,25
Σ				0	-4,5	38	17,75

wyznaczanie prognozy na okres 9:

• wyliczamy błędy prognoz ex - post na podstawie wzoru:

• średnie wartości błędów prognoz obliczamy z wzoru:

dla badanego przykładu:

prognoza przeszacowana

• wyznaczenie wariancji predykcji ex - post obliczamy z wzoru:

dla badanego przykładu:

⇒ S_p(2) = 2,52

⇒ S_p(4) = 2,11

wyniki obrazują odchylenia prognoz, ze względu na mniejszy błąd należy wybrać prognozę o parametrze 2,11.

uprzednia mediana ruchoma.

k = 1,2 ⇒ Me_t(k) =

przykład:

t	Yt	Met+1(3)	Met+1(4)
1	2	-	-
2	4	4	-
3	4	4	-
4	8	4	4
5	2	6	4
6	6	2	5
7	2	4	4
8	4	-	3

obliczenie do tabeli:

Me_t+1(3) - kolejność składników do obliczeń wpisywać rosnąco (od najmniejszej do największej).

mediana dla nieparzystej liczby składników jest składnikiem środkowym.

2,4,4 środkowa 4 czyli mediana

4,4,8 środkowa 4 czyli mediana

2,4,8 środkowa 4 czyli mediana

2,6,8 środkowa 6 czyli mediana

2,2,6 środkowa 2 czyli mediana

2,4,6 środkowa 4 czyli mediana

Me_t+1(4) - kolejność składników do obliczeń wpisywać rosnąco (od najmniejszej do największej).

mediana dla parzystej liczby składników jest średnią arytmetyczną środkowych dwóch operacji.

2,4,4,8 suma dwóch środkowych cyfr dzielona przez dwa 8:2 = 4

2,4,4,8 suma dwóch środkowych cyfr dzielona przez dwa 8:2 = 4

2,4,6,8 suma dwóch środkowych cyfr dzielona przez dwa 10:2 = 5

2,2,6,8 suma dwóch środkowych cyfr dzielona przez dwa 8:2 = 4

2,2,4,6 suma dwóch środkowych cyfr dzielona przez dwa 6:2 = 3

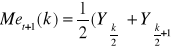
wyznaczanie kwantyli - gdy „k” jest duże:

Wykład 4 - 12.01.2002

Metody adaptacyjne cd.

1. wyrównywanie wykładnicze ma postać:

ocena trendów w okresie
jest równa:

ocena ta równa jest średniej wartości dwóch ważonych

prognoza na okres t+1 ma postać:

prognozę tę możemy również zapisać jako:

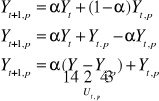
U_t - błąd prognozy

błąd prognozy okresu t+1

Sposoby wyznaczania parametru α.

W praktyce wykonujemy to w sposób arbitralny - jeśli szereg który mamy analizować przebiega w sposób stacjonarny.

Aby wyznaczyć α przyjmuje się, że:

α = 0; 0,1; 0,2; 0,3; 0,4; ........................1,0

i dla każdego α wylicza się wartości trendu np.

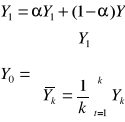
k = 1,2 ............n

następnie obliczamy błędy prognozowania U_t,p(α)

następnie wyliczamy sumy kwadratów błędów prognozowania

przykład:

Cena akcji w poszczególnych pięciu notowaniach tworzy następujący szereg.

Wyznaczyć prognozę na okres szósty.

t	Yt
1	2	2,0	-	-	-
2	4	3,6	2,0	2	4,0
3	1	1,52	3,6	-2,6	6,76
4	5	4,3	1,52	3,5	12,25
5	5	4,86	4,3	0,7	0,49
6	-	-	4,86	-
Σ					23,50

dla obliczeń założono, że

Y₀ = Y₁ a α = 0,8

sposób obliczania

suma kwadratów Q(α) wynosi Q(0,8) = 23,5

możemy teraz obliczyć wariancję predykcji ex - post

2. metoda autoregresyjna

rozważamy ciąg obserwacji od Y₁ do Y_n

współczynnik autokorelacji rzędu „k”

(ro)
i należy do przedziału <-1,1>

estymator współczynnika:

modele autoregresyjne:

funkcja autoregresyjna rzędu „g”

model autoregresyjny rzędu pierwszego zachodzi gdy:

R_k > R_k+1 k = 1,2 ................. n

i ma postać:

Współczynnik autokorelacji rzędu pierwszego mierzy następujące współzależności:

B(Y_t,Y_t-1) > 0

B(Y_t, Y_k) = 0

dla k = 2,3 .................n

Wyznaczanie prognoz jest pewna symulacja.

Podstawą jest model ekonometryczny, szczególnym jego przypadkiem jest funkcja trendu.

Wyliczenie wartości zmiennej prognozowanej i wyznaczenie błędu prognozowania.

Błąd jest nieodzowny w wyznaczaniu prognozy.

Klasyczne metody prognozowania wykorzystują wygładzanie szeregów czasowych.

Oprócz prognozy trzeba wyznaczyć błąd prognozy w 2 sposoby:

1. istnieje możliwość wyliczania błędu ex ande - podejście modelowe

2. stosuje się wyliczenie błędu ex post - podejście adaptacyjne

ex ande wykorzystywane w momencie wyznaczania samej prognozy

ex post możliwe do zastosowania kiedy wyznaczamy ciąg prognoz dotyczących kilku okresów.

KLASYCZNY LINIOWY MODEL EKONOMETRYCZNY

k

Y_t = ∑ α_i X_i + ξ_t

t=0

α_o, 1X_oi = 1 wyraz wolny, stały

k

Y_t = α₀ + ∑α_i * X_it + ξ_t

t=1

Dodatkowe warunki

Y_t i ξ_t - zmienne losowe

α₀ + ∑α_i* X_it- zmienne losowe

Zakłada się, że nadzieja matematyczna zmiennej objaśniającej będzie równa zmiennej nielosowej, ponadto dla każdego t wariancja jest równa sigma kwadrat.

Dal każdego t = h kowariancja pomiędzy składnikami są nie korelowane ze sobą.

KLASYCZNY MODEL REGRESJI

k

1E(ξ_t) = 0 → E(Y_t) = ∑ α_i X_it

t t=0

1D²(ξ_t) = 0² 1 Cov(ξ_t ξ_h) = 0

t t+h=1...n

Dla każdego t rozkład normalny

1 ξ_t ≈ η (0,0²)

t

t = 1,2,...,n n+1, n+2,n+h h = 1,2,...

h - wyprzedzenie czasowe prognozowania

Y₁, Y₂, ..., Y_n Y_n+1, Y_n+2, Y_n+h

obserwowane prognozowane

Błąd prognozy

U_t+h = Y_t+h - Y_pt+h

Y_p1t+h = f (Y₁,Y₂,...,Y_n)

y₁,y₂,...,y_n U_t+h = y_t+h - y_pt+h

Najprostszy sposób wyznaczania prognozy jest związany z modelem liniowym

Y = X_α + ξ

ξ1 Y1 1 X11 X12 . X1n

ξ2 Y2 1 X21 X22 . X2n

ξ = . Y = . X.= . . . .

. . . . . . .

. . . . . . .

ξ Yn 1 Xn1 Xn2 . Xnn

t

Metoda najmniejszych kwadratów

ϕ(α) = ( Y - Xα)^T ( Y - Xα)

a : ϕ (a) = min

a = (X^TX)^-1 X^TY

^

e = Y - Y = Y - X*a

Stopień dopasowania ocenia się za pomocą wariancji resztowej

e_t = y = ∑ α₁ * X_it

t=0

V(a) = I - (α - a) ( α - a)^T = (X^TX)^-1 δ²

V^(a) = (X^TX)^-1 S²_e

V₁₁ V₁₂ V_1n

V(a) = . . . = [V_ij] _(k+1)*(k+1)

. . .

D²(a_i) i=j =δ² 2ij

Vij= Cov (a_ia_j) i≠j =δ² 2ij

y - wynagrodzenie bieżące

y= 1970,8 -749,3x₁ + 1,6x₂ + 388,2x₃-697,9x₄ +e

stałe płeć wyagr. wykszt. rasa

pracownika przeciętne

y^

y= -3123,5+1,7x2+408,2x3+e

(701,5) (0,059) (64,220)

D^(y^i)- przeciętny zarobek

a= [∑(y_t-y) t] / [∑ (t-t)²], y = 1/n ∑y_t, t= 1/n ∑t

t=1 t=1 t=1

b= y - at, S²_e = [∑(yt - y^t)²]/ n-2

Metoda adaptacyjna - wykładnicza

D²(a) cov(a,b) 0,0751

V = = S²_e (X^TX)^-1 =

cov(a,b) D²(b) 0,0751 (2,6

1 1

• 1

. .

X = t 1

. .

. .

n 1

MODEL TRENDU

D²(Y_t^) = D^(a)t² + 2cov^(a,b)t + D²^(b) + S²_e

I_t = , y_t - Z_t

MEDIANA

1. szereg jednostopniowy

X _n+1/2 n- nieparzyste

Me =

X_n/2 +X_n/2+1 n - parzyste

2

2. szereg wielostopniowy

Me = X₀ + C₀/n₀ ( n/2 - cum_-1)

KLASYCZNY MODEL EKONOMETRYCZNY

k

Y_t = ∑ α_iX_i + ξ_t

t=0

k

Y_t = ∑α_iX_it + α₀ + ξ_t

t=1

Błąd prognozy

U_t+h = Y_t+h - Y_pt+h

Y_pt+h = f(Y₁,Y₂,...,Y_n) Y_t,p+h = ∑ ai * X_in+h

Warunek kryterium najmniejszych kwadratów

ϕ(a) = u^Tu = (y - x_a)^T(y-x_a) = min

a= (X^TX)^-1 X^Ty Y^ = Xa - model oszacowany

A^-1 = (1/detA) * D^T

Reszta

e = Y - Y^ = Y - Xa - wektor reszt

Wariancja resztowa

Kowariancja

V(a) = E (α-a)(α-a)^T = (X^TX)^-1 * δ²

V^(a) = (X^TX)^-1 * S²_e

Prognoza na okresy n+1, n+h

k

Y_p,t+h = ∑ a_i * X_in+h

i=0

Ocena błędu prognozy

k

Y_t = ∑α_iX_it + ξ_t

i=0

Liniowa funkcja trendów

Y_t = a_t + b + ξ_t

Błąd prognozowania ex ante

U_n+h = Y_n+h - Y_p,n+h

k k

E(U_n+h) = E(Y_n+h) - E(Y_p,n+h) = ∑α_iX_i,n+h - ∑E(a_i) * X_i,n+h = 0

i=0 i=0

Nadzieja matematyczna predykatora = 0 - predykator jest nieobciążony

Błąd losowy prognozowania - wyrażony wariancją (nie jest mniejszy od wariancji składnika losowego)

D²(U_n+h) = D²(Y_n+h - Y_p,n+h) = D²(Y_n+h) + D²(Y_p,n+h)

Względny ład prognozy

γ(U_n+h) = * 100%

γ (un+h) ≤ γ %

Horyzont predykcji

H:max γ(U_n+h) ≤ γ₀

H:max D²(U_n+h) ≤ d₀

Metody wyrównywania wykładniczego

Y_t = α_y-1 + α(1-α)y_t-2 + α(1-α)² y_t-3

Y^_t+1 = α_yt + (1-α)y_t^

Ut(α) = yt - yt^(α)

U =1/m ∑ut

Wariancja ex post prognozowania

S²_u = 1/m ∑ u²t

t

S_u = √S²u

Np. γ₉ = S_k/y₉^ (względny błąd prognozy / ostatnie nasze prognozy y₉^)

Ocena parametrów trendu liniowego wyznacza metody NMK.

y_t = e^α+βt lub y_t = αβ^t β>0

β>1 rosnąca

β<1 malejąca

Wielomian drugiego stopnia (parabole)

y_t = α_t + α₁t α₂t² α2>0

Funkcja potęgowa

y_t = αt^β 0<β<1

Funkcja liniowo - odwrotnościowa

y_t = α + β/t β<0

Funkcja ilorazowa

y_t = αt/ β+t

Funkcja logistyczna

y_t = α / 1+ βe - δt α δ>0, β>1

Model potęgowy

y_t = αt^β

Średnie ruchome nieparzyste liczby składników

Średnie ruchome parzysta liczba składników

Ruchome średnie

Y_t+1(k) = 1/k ∑Y_i

Y_t+1(1) = 1*Y_t = Y_t

Y_t+1(2) = ½ (Y_t-1 + Y_t)

Metody wyznaczania prognoza pomocą średnich ruchomych.

Wskaźnik średniego indeksu wyznaczonych cech

Indeks zmiennej o podstawie stałej

I_t/c = y_t/y_c I_t/c = d_t/c + 1 d_k/c = (y_t - y_c)/y_c

Indeks o podstawie łańcuchowej stosunek do okresu poprzedniego

I_t = y_t/ (y_t - 1) I_t = d_t + 1 d_t = (y_t - y_t-1) / y_t-1

d = I + 1 I = √ I₁ * I₂ * I₃ * ... * I_n+1 * I_n

I₁ * I₂ * I₃ = y₁/y₀ * y₂/y₁ * y₃/y₂ = y₃/y₀ = I_3/0

I_t = y_t / y_{t -1}

y_t = I₁ * y_t-1

I_k-1 = y_t-1/y_t-2

y_t-1 = I_k-1 * y_t-2

y_t = I_tI_k-1y_t-2

y_t = I_tI_x-1 I_t-2 y_t-3

y_t= I * y_t-1

Prognoza y_t = I₂y_t-2

y_t-1 = Iy_t-2

y_k = I³y_t-3

Ogólny wzór na metodę prognozowania - wskaźnik indeksu średniego

y_t = I_k * y_t-k

t	yt
1	6	-1,66	-	-
2	10	1,30	-	-
3	13	1,00	-	-
4	13	1,07	-	--
5	14		-	0,64	0,40
6	18		17,36	-1,5	2,25
7	20		21,50	-4,6	21,16
8	22		26,60	-8,98	80,64
9	24		32,98	15,08	104,45
10	24			14,44

Stopień pierwiastka jest równy liczbie wymnażanych indeksów

I = ⁴√ 2,33 = 1,24

y₆ = I * y₅ = 1,24 * 14 = 17,36

y_t = I^k * y_t-k

y_t+k = I^k * y_t

y₇= I² * y₅ = (1,24)² * 14 = 1,24*17,36=21,50

y₈ = I³ * y₅ = I * y₇ = 1,24*21,50=26,60

y₉ = I⁴ * y₅ = I * y₈ = 1,24*26,60=32,98

Ex post

e_t = y_t - y_t

e = 1/m ∑ e_t

e = -1/4 * 14,44 = -3,61

Wartości zmiennej prognozowanej są przeszacowywane o 3,61.

Dostajemy tą prognozę obciążona błędem systematycznym.

Błąd przeciętny prognozowania wyliczmy na podstawie ex post

S²_k = 1/m ∑ e²_t = ¼ * 104,45 = 26,11

Se = √ 26,11 = 5,11

Średni błąd prognozowania V_k

V_t = S_e / y_t

V₈ = 5,11/26,60 = 0,19

V₆ = 5,11/17,36 = 0,29

t	yt	yt	ξt = yt-yt	h	yt,h	gt,h	yt
1	1	7	-6	1	1,67	0,14 (1/7)	3,64 (7*0,52)
2	8	9	-1	2	7,34	0,88 (8/9)	8,10 (9*0,9)
3	12	11	1	3	13,66	1,09 (12/11)	12,32
4	17	13	4	4	17	1,3	15,86
5	9	15	-6	1	33	0,6
6	16	17	-1	2		0,94
7	22	19	3	3		1,15
8	26	21	5	4		1,23
9	19	23	-4	1		0,82
10	22	25	-3	2		0,88
11	31	27	4	3		1,14
12	33	29	4	4		1,13
13		31			25,67
14		33			31,34
15		35			27,66
16		37			41,33

prognozy

y_t = 2t + 5 + ξ_t

MODEL SZEREGU KLASOWEGO

Szereg czasowy

y_t = f(t) + a(t) + ξ_t

funkcja odzwierciedlająca

wahania sezonowe

ξt - losowe wahania w tym zadaniu - addytyczne

y_t = f(k) b(t) - ξ_t

Ocena wskaźnika sezonowości ah

T - bieżący identyfikator danych

y_t,h = f(t) + a_h + ξ_t

a_h = 1/m∑ξ _t,h

a₁ = 1/3 (ξ1 + ξ5 + ξ9) = 1/3 ( -6-6-4) = -16/3 = -5,33

a₂ = 1/3 (ξ2 + ξ6 + ξ10) = 1/3 (-1-1-3) = -5/3 = -1,66

a₃ = 1/3 (ξ3 + ξ7 + ξ11) = 1/3 (1+3+4) = 8/3 = 2,66

Model

y_t,h = y_t+ a_h

Średni wskaźnik sezonowości dla kwartału będziemy dodawać do funkcji trendu

y_1,1 = 7-5,33 = 1,67

Błąd prognozy - nie obliczmy bo za dużo zmiennych

MODEL MULTIPLIKATYCZNY

y_t = f(t)b(t)ξ_t

y_t,h - f(k) b_h ξ_t,h

Oceny wskaźników sezonowości

bn = 1/m ∑ y_t,h/y_t

g_t,h = y_t,h / y_t

b₁ = 1/3 (0,14+0,6+0,82) = 0,52

b₂ = 1/3 (0,88+0,04+0,88) =0,9

b₃ = 1/3 (1,09+1,15+1,14) = 1,12

b₄ = 1/3 (1,3+1,23+1,13) = 1,22

Ocena funkcji

y_t = y_t - b_h

Struktura czasowa wykazuje wahania sezonowe. Trend rosnący z wahaniami sezonowymi.

Czy do tego by pasował model multipliatyczny?

W tym przypadku by pasowała funkcja trendu wyznaczona na podstawie średnich.

1. Podstawowe własności modeli ekonometrycznych (estymacja modelu, parametry określające zgodność modelu z danymi i wariancja resztowa), współrzędne zbieżności, determinacji, współrzędne funkcji regresji ≠0.
   
   Model ekonometryczny z 1 zmienną lun 2 lub 3 wymaga prognozy na podstawie podanego modelu. Wartości zmiennej objaśnianej.

2. Metoda najmniejszych kwadratów - estymacja trendu liniowego kwadratów nieliniowych.
   Trend z jedna zmienną objaśniającą - czas.
   !!! Oszacować parametry trendu
   Wariancja rusztowa - błąd prognozy (współrzędne zbieżności, determinacja)

3. Metody klasyczne - najstarsze

4. Wyznaczanie trendu metodą najmniejszych kwadratów, metody adaptacyjne - średnie scentrowane (mediany)

5. Średnie ruchome scentrowane

6. Wahania sezonowe

7. Ocena dokładności składników losowych za pomocą wariancji ex post, wskaźniki prognozowania

MODELOWANIA SZEREGÓW CZASOWYCH

Metoda autoregesyjna

Y₁,Y₂,...,Y_t, ..Y_n - zależności liniowe autokorelacji

Autokorelacja do badania stopnia zależności.

Yt	Yt-1	Yt-2	Yt-Y	Yt-1-Y	(Yt-Y)^2	(Yt-Y)(Yt-1Y)
2	4	0	0,9	2,9	0,81	2,61
4	0	0	2,9	-1,1	8,41	-3,19
0	0	1	-1,1	-1,1	1,21	1,21
0	1	0	-1,1	-0,1	1,21	0,11
1	0	-	-0,1	-1,1	0,01	0,11
0	-	-	-1,1		1,21	∑0,85
					∑12,86

Model autoregresji

t

Y_t = α₀ + ∑ α_dY_t-1 + ξ _t

d-1

t h

Y_t = α₀ + ∑ α₁γ_t-1 + ∑βx_t + ξ_t

• t-1

PROGNOZY I SYMULACJE TESTY Z NASZEGO EGZAMINU

TEST 1

1. Zapisać i wyjaśnić własności funkcji opisującej trend paraboliczny

2. Trend wzrostu sprzedaży wody mineralnej ma postać Yt= 2t+180, gdzie t= 1,2,3... Kwartalne addytywne wskaźniki sezonowości sprzedaży wody wynoszą -50, -10, 40, 20 odpowiednio dla kwartałów I, II, III, IV. Prognozy na kolejne kwartały roku 10 wynoszą odpowiednio:

3. Notowania kursów akcji w kolejnych okresach wynoszą: 20, 30, 40, 50, 60. Zcentrowane średnie ruchome dwu-okresowe określa ciąg:

4. Współczynnik determinacji trendu liniowego wyznaczonego na podstawie 12 obserwacji wynosi 0,95, a suma kwadratów odchyleń zmiennej objaśnianej od jej średniej wynosi 20. Wartość wariancji resztowej jest równa:

5. W latach od 1 do 10 trend wzrostu sprzedaży pewnego towaru ma postać Yt= t²-2t+80 Średni względny błąd predykcji ex-ante poziomu sprzedaży na rok 12 jest równy 4%. Jaka jest wartość wariancji predykcji ex-ante na rok 12.

6. W miesiącach od stycznia do kwietnia zaobserwowano następujące indeksy łańcuchowe tygodniowych dochodów sklepu (w%): 114,116,116,118. Jakie było średnie tempo zmian. Wyznaczyć prognozę na podstawie indeksu średniego na miesiąc lipiec, gdy wiadomo, ze dochód sklepu w kwietniu wynosił 10 tyś. Zł.

7. W miesiącach od stycznia do lipca zaobserwowano nast. Miesięczne wydatki (w zł): 4,5,8,10,12,14,15. Oszacować trend metodą najmniejszych kwadratów na podstawie danych od stycznia do kwietnia i wyznaczyć na jego podstawie prognozy wydatków do lipca. Wyliczyć i zinterpretować średnią i wariancje ex-post błędów prognoz.

TEST 2

1. Trend wzrostu sprzedaży wody mineralnej ma postać Yt = 2t+180, gdzie t= 1,2,3.... Kwartalne multiplikatywne wskaźniki sezonowości sprzedaży wody wynoszą 120%, 50%, 140% i 90% odpowiednio dla kwartałów I, II, III, IV. Prognozy na kolejne kwartały roku 10 wynoszą odpowiednio:

2. Zapisać i wyjaśnić funkcje opisującą trend wykładniczy (*potęgowy)

3. Notowania kursów akcji w kolejnych okresach wynoszą 2,3,4,5,3. Średnie ruchome trój-okresowe określa ciąg:

4. Współczynnik zbieżności trendu liniowego wyznaczonego na podstawie 12 obserwacji wynosi 0,1, a wariancja resztowa 2. Wówczas suma kwadratów odchyleń zmiennej objaśnianej od jej średniej wynosi:

5. W latach od 1 do 10 trend wzrostu sprzedaży pewnego towaru ma postać Yt=t²-2t+80. Wariancja predykcji ex-ante wynosi 16 na rok 12. Średni względny błąd predykcji ex-ante poziomu sprzedaży na rok 12 jest równy:

6. W miesiacach od stycznia do kwietnia zaobserwowano następujące tygodniowe zyski sklepu (w tyś zł) 4,5,6,6,8,. Jakie było średnie tempo zmian . Wyznaczyć prognozę na podstawie indeksu średniego na miesiąc czerwiec

7. W miesiącach od stycznia do kwietnia zaobserwowano następujące miesięczne wydatki (w zł) 4,6,10,8. na podstawie trendu :y=3t+1 wyznaczyć drugi ciąg prognoz na miesiące od stycznia (t=1) do kwietnia. Wyliczyć średnią oraz wariancje ex-post błędów. Wyliczyć współczynniki Theila dla obu metod prognozowania.

TEST 3

1. W latach od 1 do 10 trend wzrostu sprzedaży pewnego towaru ma postać Yt=t²-2t+80. Wariancja predykcji ex-ante wynosi 16 na rok 12. Średni względny błąd predykcji ex-ante poziomu sprzedaży na rok 12 jest równy:

2. Trend wzrostu sprzedaży wody mineralnej ma postać Yt=2t+180 gdzie t=1,2,3,....Kwartalne multiplikatywne wskaźniki sezonowości sprzedaży wody wynoszą 50%, 100%, 200% i 80% Odpowiednio dla kwartałów I, II, III i IV. Prognozy na kolejne kwartały roku 10 wynoszą odpowiednio.

3. Zapisać i wyjaśnić funkcję opisującą trend potęgowy.

4. Notowania kursów akcji w kolejnych okresach wynoszą 2,3,4,5,3. Zcentrowane średnie ruchome trój-okresowe określa ciąg.

5. Współczynnik zbieżności trendu liniowego wyznaczonego na podstawie 12 obserwacji wynosi 0,2 a wariancja resztowa 2. Wówczas suma kwadratów odchyleń zmiennej objaśnianej od jej średniej wynosi:

6. W miesiącach od stycznia do kwietnia zaobserwowano następujące tygodniowe zyski sklepu (w tyś zł): 4,5,6,6,8. Jakie było średnie tempo zmian. Wyznaczyć prognozę na podstawie indeksu średniego na miesiąc czerwiec.

7. W kolejnych miesiącach zaobserwowano następujące tygodniowe wydatki (w zł) 4,6,4,8,5,6 Wyznaczyć ciąg prognoz metodą średnich ruchomych 3-składnikowych. Wyliczyć średnią oraz wariancje ex-post błędów. Wyliczyć współczynniki Theila dla obu metod prognozowania.

TEST 4

1. Zapisać i wyjaśnić własności funkcji opisującej trend logarytmiczny .

2. Trend wzrostu sprzedaży piwa ma postać : Yt=2t+10, gdzie t=1,2,3,.... Kwartalne addytywne wskaźniki sezonowości sprzedaży wody wynoszą -5,-1,4,2 odpowiednio dla kwartałów I, II, III, IV. Prognozy na kolejne kwartały roku 10 wynoszą odpowiednio:

3. Notowania kursów dolara względem złotego w kolejnych dniach wynoszą 4,3,4,5,60. Uprzednie średnie ruchome dwu-okresowe określa ciąg:

4. Współczynnik determinacji trendu logistycznego wyznaczonego na podstawie 12 obserwacji wynosi 0,95 a suma kwadratów odchyleń zmiennej objaśnianej od jej średniej wynosi 20. Wartość wariancji resztowej jest równa.

5. W latach od 1 do 10 trend wzrostu sprzedaży pewnego towaru ma postać: Yt=t²-2t+80 Średni względny błąd predykcji ex-ante poziomu sprzedaży na rok 12 jest równy 4%. Jaka jest wartość wariancji predykcji ex-ante na rok 12.

6. W miesiącach od stycznia do kwietnia zaobserwowano nast. Indeksy łańcuchowe tygodniowych dochodów hurtowni, (w%): 110,110,120,120 Jakie było średnie tempo zmian. Wyznaczyć prognozę na podstawie indeksu średniego na miesiąc lipiec , gdy wiadomo, że dochód sklepu w kwietniu wynosił 100 tyś zł.

7. W miesiącach od stycznia do lipca zaobserwowano nast. miesięczne wydatki (w zł) 4,5,8,10,12,14,15 . Oszacować metodą najmniejszych kwadratów trend na podstawie danych od stycznia do kwietnia i wyznaczyć na jego podstawie prognozy wydatków do lipca. Wyliczyć i zinterpretować średnią i wariancję ex-post błędów prognoz.

PROGNOZOWANIE I SYULACJA

-STRONA 43 -

Parametry

Obserwacje zmiennych objaśniających (egzogeniczne)

Składnik losowy = objaśnia wpływ czynników niewyjaśnionych

0

ξ

S²_e = e^Te *

1

n-k^-1

1

n-1

n

S²_e = ∑ e²_k

t=1

1

n-k^-1

X₀ - początek przedziału mediany

C₀ - długość przedziału mediany

n₀- liczba przedziału mediany

cum_-1 - liczba kumulacji przedziału poprzedzającego przedział mediany

S²_e = e^Te

1

n-k-1

1

n-1

n

S²_e = ∑ e²_t

t=1

1

n-k-1

e_t = y_i - ∑α_iX_it

D(U_n+h)

Y_p,n+h

h- wyprzedzenie czasowe

a=

∑yt -y)t

∑(t-t)²

b = y - at

n

y = ∑yt

t=1

1

n

n

t = 1/n ∑t

t=1

S²_e =

∑(y_t-y_t)²

n-2

t+(k-1/2)

Y_t(k) = ∑Yi

i=t-(k-1/2)

1

k

t-(k/2-1)

Y_t(k) = (1/2Y_t-k/2 + ∑Yi + 1/2Y_{t +k/2})

i=t-(k/2+1)

1

k

I = √ I₂ I₃ I₄ I₅

4

I = √ = √

4

y₂ y₃ y ₄ y₅

y₁ y₂ y₃ y₄

4

y₅

y₁

4

0

-2

-4

-6

1 2 3 4 5 6 7 8 9 10 11 12

Średni wskaźnik sezonowości modelu multiplikatycznego

Żeby policzyć tak jak myśmy to zrobili to tak powinno to wyglądać

NASZ PRZYPADEK

stałe

λ =

Cov (Y_t, Y_t-1)

D(Y_t) D(Y_t-1)

D²(Yt) = δ²

t

λt = const

t-1

γd =

C_t,t-d = ∑(Y_t-Y)(Y_t-1-Y)

t

S2t-d = ∑(Y_t-1-Y)²

t

Y= ∑Y_t

t

γd =

C_t,t-1 = ∑(Y_t - Y)(Y_t-1 - Y)

C_t,t-d

S_t, S_t-d

1

n-d

1

n-d

1

n

C_t,t-d

S²_t

1

n-1

P, gdy y = 1

1 - p, gdy y = 0

P_t, gdy y = 1

1 - p_t, gdy y = 0

rozkład normalny

rozkład Studenta

---