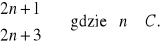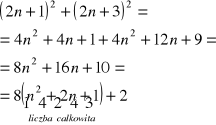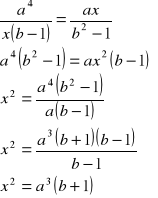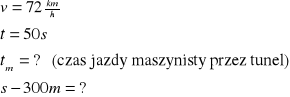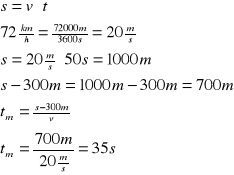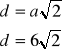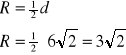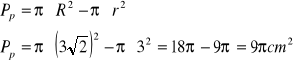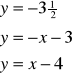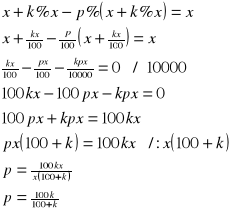KLUCZ

II Wojewódzki Konkurs Matematyczny dla uczniów gimnazjum

eliminacje szkolne 2001/2002

• Uczeń ma wybrać i rozwiązać pięć spośród sześciu zadań.

• Uczeń może maksymalnie uzyskać 30 punktów.

• Wszystkie zadania są tak samo punktowane ( po 6 punktów ).

• Do etapu rejonowego kwalifikuje zdobycie co najmniej 27 punktów, co stanowi 90% punktów możliwych do uzyskania za poprawne rozwiązanie pięciu zadań.

Nr zad.	Rozwiązanie	Punktacja
1.	Dwie kolejne liczby nieparzyste: Suma kwadratów tych liczb: Przekształcenie wyrażenia: Iloczyn liczby 8 przez dowolną liczbę całkowitą jest podzielny przez 8, więc liczba postaci przy dzieleniu przez 8 daje resztę 2.	1p. 1p. 2p. 2p. łącznie 6p.
2.	P = ? P = Pole kwadratu wynosi .	1p. 1p. 1p. 1p. 1p. 1p. łącznie 6p.

Nr zad.	Rozwiązanie	Punktacja
3.	300 m s - 300 m s Długość tunelu wynosi 700m. Maszynista jechał przez tunel 35 s.	1p. 1p. za zamianę jednostek prędkości 1p. 1p. 1p. 1p. łącznie 6.
4.	Pole pierścienia kołowego wynosi .	1p. 1p. 1p. 1p. 1p. 1p. łącznie 6p.

Nr zad.	Rozwiązanie	Punktacja
5.	A = ( -1, -5 ), B = ( 2, -5 ), C = ( 2, -2 ), D = ( -1, -2 ) Równania funkcji, których wykresy są osiami symetrii tego czworokąta: Równanie prostej, która jest osią symetrii ale jej wykres nie przedstawia funkcji:	1p. za umieszczenie danych na rysunku, 1p. za zaznaczenie osi symetrii. 3p. po 1p. za wzór każdej funkcji. 1p. łącznie 6p.
6.	x - początkowa cena towaru, k% - procent podwyżki ceny, p% = ? (procent obniżki ceny) Cena towaru po podwyżce: x + k% x Cena towaru po obniżce: x + k% x - p% ( x + k% x ) Rozwiązanie równania: Cenę należy obniżyć o .	1p. 1p. 1p. 1p. 1p. 1p. łącznie 6p.

1

Hanna Kozłowska, Katarzyna Matuszek, Antonina Wiącek

Gimnazjum nr 27 z Oddziałami Integracyjnymi w Poznaniu

a

y

x

x

a

R

r

d

a = 6 cm

r =

r = 3 cm

x

D

C

B

A

---