Wyznaczanie prędkości dźwięku w powietrzu
metodą badania przesunięcia fazowego
Rozchodzenie się dźwięku odbywa się w postaci fali mechanicznej i może mieć miejsce tylko w ośrodku sprężystym. Jeżeli pewien element ośrodka, którego cząstki są ze sobą wzajemnie związane, pobudzimy do drgań, wówczas energia drgań tego elementu będzie przekazywana do punktów sąsiednich i wywoła w nich drgania. Proces rozchodzenia się drgań nazywamy falą . Charakter fali rozchodzącej się w ośrodku zależy od jego właściwości sprężystych. Najczęściej spotykanym ruchem drgającym jest ruch harmoniczny, w którym wychylenie y zmienia się w czasie t wg. równania:
![]()
gdzie: A-amplituda, ω-częstość kołowa, - faza początkowa
Faza początkowa określa stan ruchu w chwili t=0 i jest obierana w dowolny sposób. Jeżeli fala biegnie w kierunku osi x , wówczas kolejne punkty ośrodka pobudzane są do drgań i osiągają tę samą fazę z pewnym opóźnieniem. Prędkość przesuwania się wychylenia(zaburzenia)o stałej fazie jest prędkością rozchodzenia się fali.
Wychylenie y dowolnej cząstki w chwili t, w odległości x od źródła drgań opisane jest funkcją falową :
gdzie: ω- częstość kołowa ; - liczba falowa,
- długość fali, - faza w punkcie x=0 i w chwili t=0.
Równanie fali jest podwójnie okresowe: względem czasu i przestrzeni. Przy ustalonej wartości x opisuje ono drgania cząstki wokół położenia równowagi - drgania te są periodyczne z okresem T. Ustalając w poprzednim równaniu czas otrzymujemy zależność wychylenia cząstek od ich położenia w określonej chwili - zależność ta przedstawia kształt fali. Odległość między najbliższymi punktami posiadającymi tę samą fazę nazywamy długością fali.
Związek między długością i okresem jest prędkością fali:
Prędkość fali w powietrzu
Ogólne wyrażenie określające prędkość rozchodzenia się fal podłużnych w ośrodku ciągłym ma postać:
gdzie: E- moduł Younga ośrodka, - jego gęstość.
Przekształcając podstawową postać prawa Hook'a możemy napisać: (1)
gdzie oznaczają różniczkowe zmiany ciśnienia i objętości gazu o objętości V
Drgania dźwiękowe zachodzą tak szybko, że ściskanie i rozrzedzanie gazu można uważać za procesy adiabatyczne, wobec czego zmiana stanu gazu zachodzi zgodnie ze wzorem Poissona:
gdzie - jest stosunkiem ciepła właściwego przy stałym ciśnieniu do ciepła właściwego przy stałej objętości.
Różniczkując powyższy wzór otrzymujemy:

Podstawiając uzyskaną wartość do równania (2), a następnie uwzględniając otrzymaną w ten sposób postać modułu Younga w równaniu (1), wyrażamy prędkość fali podłużnej wzorem:
Stosując równanie stanu gazu doskonałego we wzorze na gęstość otrzymamy:
gdzie: n - ilość moli gazu, R - stała gazowa, T - temperatura.
n można wyrazić jako stosunek całej masy gazu m do masy 1 mola μ : n = m / μ.
Uwzględniają powyższe w ostatnim równaniu wstawiamy do równania (3) i otrzymujemy wzór określający prędkość dźwięku w zależności od rodzaju gazu i temperatury:
Aby obliczyć prędkość skorzystamy ze wzoru :
Częstotliwość odczytamy bezpośrednio z generatora akustycznego. Długość fali obliczymy dzięki zjawisku figur Lissajous obserwowanych na oscyloskopie, a których kształt zależy od stosunku częstotliwości różnicy faz drgań składowych. W tym przypadku częstotliwości obu drgań są równe, więc o kształcie figur decyduje różnica faz głośnika i mikrofonu. Kształt figury Lissajous'a będzie on taki sam dla wszystkich położeń mikrofonu różniących się o całkowitą wielokrotność długości fali.
Wybieramy odpowiednią częstotliwość, a następnie przesuwając mikrofon w stosunku do głośnika znajdujemy położenia, w których obraz na ekranie oscyloskopu jest linią prostą o takim samym współczynniku nachylenia. Odnotowujemy położenia mikrofonu, następnie obliczamy długość fali jako różnicę pomiędzy takimi samymi obrazami, obliczamy średnią, a następnie prędkość dźwięku z powyższego wzoru.
Obliczenia
Dla dźwięku o częstotliwości f = 2 [kHz]
l [m] |
λ = ln-1 - ln [m] |
v = λ * f [m/s] |
0,124 |
- |
- |
0,302 |
0,178 |
356 |
0,47,8 |
0,176 |
352 |
0,653 |
0,175 |
350 |
0,812 |
0,159 |
318 |
![]()
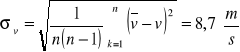
Dla dźwięku o częstotliwości f = 3 [kHz]
l [m] |
λ = ln-1 - ln [m] |
v = λ * f [m/s] |
0,159 |
- |
- |
0,317 |
0,158 |
474 |
0,523 |
0,206 |
618 |
0,689 |
0,166 |
498 |
0,892 |
0,203 |
609 |
![]()
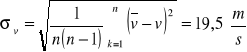
Dla dźwięku o częstotliwości f = 4 [kHz]
l [m] |
λ = ln-1 - ln [m] |
v = λ * f [m/s] |
0,143 |
- |
- |
0,177 |
0,103 |
412 |
0,356 |
0,11 |
440 |
0,46 |
0,104 |
416 |
0,565 |
0,105 |
420 |
0,676 |
0,111 |
444 |
0,768 |
0,0692 |
396 |
895 |
0,127 |
508 |
![]()
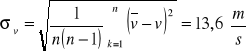
Dla dźwięku o częstotliwości f = 5 [kHz]
l [m] |
λ = ln-1 - ln [m] |
v = λ * f [m/s] |
0,098 |
- |
- |
0,177 |
0,079 |
360 |
0,255 |
0,078 |
390 |
0,335 |
0,08 |
400 |
0,419 |
0,084 |
420 |
0,49 |
0,071 |
355 |
0,58 |
0,09 |
450 |
0,661 |
0,081 |
405 |
0,753 |
0,092 |
460 |
0,819 |
0,066 |
330 |
Ostatni wynik odrzucamy jako obarczony błędem grubym.
![]()
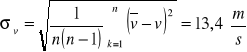
średnia szybkość dźwięku ![]()
≈ 432,75 [m/s]
odchylenie standardowe średniej szybkości dźwięku:
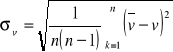
= 42,97[m/s]
Obliczam prędkość dźwięku ze wzoru:

Przyjmuję: ![]()
![]()
![]()
![]()
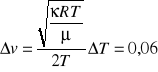
[m/s] gdzie ![]()
Wnioski
Wartość uzyskana pomiarami: v = 432,75 ± 42,97 [m/s]
Wartość obliczona ze wzoru: v = 345,83 ± 0,06 [m/s]
Wartości najbliższe wystąpiły dla f = 2 kHz i f = 4 kHz
Otrzymane wynik odbiega od wartości tablicowej. Przyczyny tego należy szukać w metodzie przeprowadzania doświadczenia a także w niedokładności pomiarów. Odczyt położenia mikrofonu względem źródła dźwięku jest ma*o dokładny.
Wyszukiwarka