Z3
1. Rozłożyć na czynniki nierozkładalne wielomian :
a)![]()
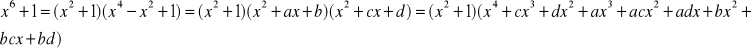
c+a=0 a=-c a=-c a=-c a=-c
d+ac+b=-1 d=-1-b+a 1/b=-1-b+a b=-b-b +a b 0=-2b-b +a b
ad+bc=0 ad-ab=0 a/b-ab=0 a/b-ab=0 a/b
bd=1 d=1/b d=1/b d=1/b
b=1
c=![]()
d=1
a=![]()
![]()
lub drugi sposób
![]()
![]()
![]()
z= -1 =![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
2. Sprawdzić czy funkcje wymierne są ułamkami prostymi :
a)![]()
nad R -to jest ułamek prosty bo w R nie można rozłożyć mianownika ułamka na czynniki (mianownik nie zeruje się)
b)![]()
nad R - to nie jest ułamek prosty bo da się go rozszerzyć o (![]()
)
c)![]()
nad C - to nie jest ułamek prosty bo mianownik da się rozłożyć na czynniki (x-i)(x+i)
d)![]()
nad Q- to jest ułamek prosty bo mianownik nie da się rozłożyć na czynniki wymierne
4. Rozłożyć na ułamki proste nad R funkcję wymierną ![]()
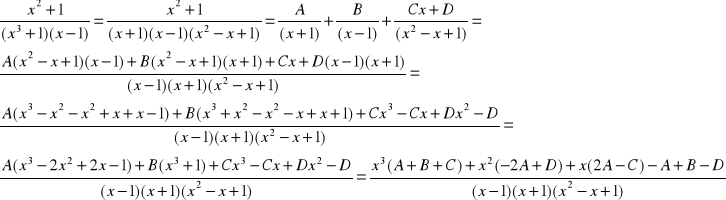
A+B+C=0 A+B=-C A+B=-2A B=-3A B=-3A B=1
D-2A=1 D=2A+1 D=2A+1 D=2A+1 D=2A+1 D=1/3
2A-C=0 C=2A C=2A C=2A C=2A C=-2/3
-A-D+B=1 -A-2A-1+B=1 -3A+B=2 B=2+3A -6A=2 A=-1/3
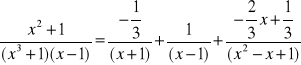
Praca domowa1
Wykazać ,że: 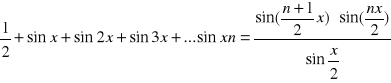
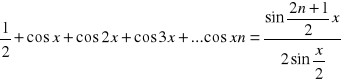
Korzystam z wcześniej dowiedzionego wzoru :
![]()
gdzie z-liczba zespolona ![]()
Wstawiam do wzoru:
![]()
Korzystam z wzoru Moivre'a:
Potem rozpisuję wzór na dwa szeregi , przekształcam prawą stronę,(ruguję część urojoną w mianowniku,wymnażam, grupuję na częśc rzeczywistą i część urojoną, stosuję wzory na cosinus sumy dwóch kątów i sinus różnicy dwóch kątów,odzielnie przekształcam
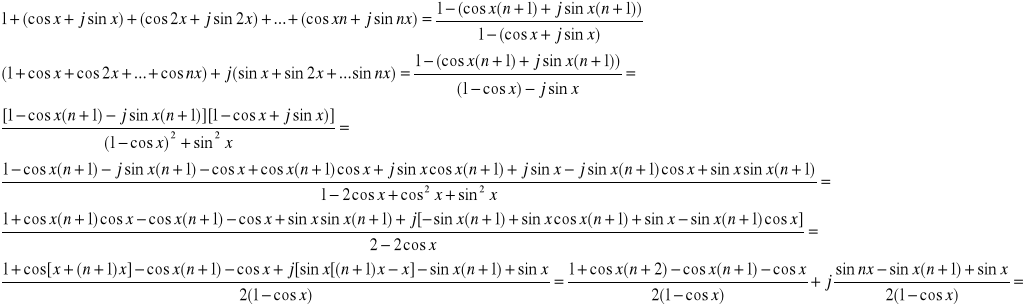
oddzielnie przekształcam część rzeczywistą (stosuję wzór na różnicę cosinusów)
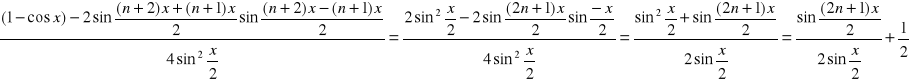
przenoszę ½ na lewą stronę i otrzymuję :
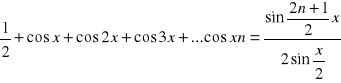
c.n.d
oddzielnie przekształcam część urojoną (stosuję wzór na różnicę sinusów)
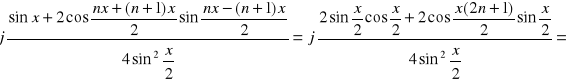
Z4
1.Wykaż, że każdy układ wielomianów ![]()
gdzie i= 0, 1,2...n takich , że stopień![]()
jest bazą przestrzeni R![]()
![]()
![]()
- zbiór wielomianów tworzy przestrzeń
baza: ![]()
bo każdy wielomian można utworzyć z tej kombinacji i wielomiany te są liniowo niezależne
![]()
![]()
![]()
![]()
-tworzą bazę dla przestrzeni R ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
są liniowo niezależne
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
2.Niech ![]()
. Czy zbiór![]()
![]()
![]()
![]()
jest podprzestrzenią przestrzeni liniowej ![]()
? Jeśli tak , podać jej nazwę i wymiar.
![]()
![]()
![]()
![]()
Kolokwium1
1. Obliczyć ![]()
lub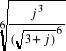
lub![]()
2. Dane jest przekształcenie liniowe ϕ: R3 → R3 takie, że ϕ((0,1,1)=(1,1,3) i ϕ((1,1,1)=(1,2,3) i ϕ((1,2,1)=(2,2,3) Znaleźć wzór postaci ϕ ((x,y,z))=(a1x+b1y+c1z,a2x+b2y+c2z,a3x+b3y+c3z)
3.Znaleźć jądro przekształcenia ϕ: R3 → R3 oraz jego wymiar, jeżeli ϕ((x,y,z))=(y,x+z,3z) lub ϕ((x,y,z))=(y,3y,x+z) lub ϕ((x,y,z))=(x+y,z,3z)
Z6
1. Sprawdzić, czy poniższe macierze dadzą się pomnożyć i ewentualnie obliczyć iloczyny AB i BA.
A =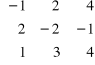
, B = 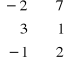
A = ![]()
, B = 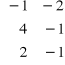
2. Dane jest ϕ:R3→R2, ϕ((x,y,z)) = (x+y-z, 2x-3y+2z) i ψ:R2→R4, ψ ((x,y)) = (x-y, x+y, 2x-y, x+2y). Obliczyć ψϕ ((x,y,z), znajdując macierze ϕ i ψ w bazach zerojedynkowych.
3. Znaleźć metodą macierzową wzór przekształcenia ϕ:R3→R2 postaci ϕ ((x,y,z)) = (a1x + b1y + c1z, a2x + b2y + c2z, a3x + b3y + c3z) jeśli wiadomo, że ϕ ((1,1,1)) = (2,1,3), ϕ ((1,1,0)) = (1,1,2) i ϕ ((1,0,0)) = (3,2,1)
4. Dana jest macierz 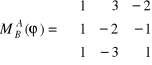
, gdzie A = ((1,0,0), (1,1,0), (1,1,1)), B = ((1,2,3), (3,1,2), (1,1,0)). Obliczyć ϕ((1,2,3))
Z7
1. Znaleźć wszystkie minory stopnia 2 macierzy 
. Ile jest minorów stopnia k macierzy A = [aji]mxn ?
2. Obliczyć det A, gdzie A = 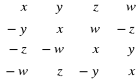
, gdzie x,y,z,w ∈ C.
3. Obliczyć 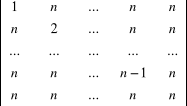
4. Wykazać indukcyjnie, że:
Odpowiedzi
3.ϕ ((x,y,z)) = (-x+4y-3z, 3x-2y+z, 5y-4z, 5x-5y+3z)
4.ϕ ((x,y,z)) = (3x-2y+z, 2x-y, x+y+z)
5.ϕ ((1,2,3)) = (-11, -17, -34)
Wyszukiwarka