WEKTORY

Wektor to dwa punkty - początek i koniec, mówią nam one jego kierunku, zwrocie i wartości.

• Kierunek jest to prosta, na której leży ów wektor

• 
  Zwrot określa nam, który punkt symbolizuje początek wektora

• Wartość jest to tzw. długość wektora (odległość pomiędzy punktem początkowym, a końcowym) wyrażana jest w konkretnych jednostkach.

Wektory znalazły niezwykłe zastosowanie w fizyce. Służą one do opisywania jakiegoś zjawiska. Przykłady wektorów:

• Wektor przemieszczenia (jak zmienia się położenie ciała)

• Wektor prędkości (zmiana położenia w czasie)

• Wektor przyspieszenie (zmiana prędkości w czasie)

Niekiedy wektor przemieszczenia jest mylony z wektorem prędkości. To nie jest to samo! Prędkość mówi nam jak szybko zmienia się położenie (w czasie).

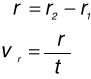
Inne przykłady wektorów:

• Wektor siły

• Wektor momentu siły

Na lekcjach fizyki w gimnazjum, wielkości (mimo iż będące wektorami) nie były oznaczane w jakiś specjalny sposób. To nie do końca poprawne. Wektory należy oznaczyć, dorysowując niewielką strzałkę nad wielkością, dla przykładu:

Zarówno siła (F), jak i przyspieszenie (a), to wektory.

Ale zaraz, w powyższym równaniu, siła jest iloczynem wektora i skalara. Czy jest to dozwolone? Tak! W wielu równaniach spotykamy się z mnożeniem wektora przez liczbę.

• Gdy jest ona dodatnia, wartość (długość) wektora powiększamy (pomniejszamy) tyle razy ile wynosi ta liczba.

• Gdy jest ona ujemna, wektor powiększamy tyle razy, ile wynosi moduł tej liczby. W tym przypadku zmienia się także zwrot wektora. Kierunek pozostaje bez zmian.

Czasem na ciało działa wiele sił lub też porusza się w taki sposób, że opisujemy to używając kilka wektorów prędkości. Aby móc określić wypadkową tych prędkości (zastąpienie ich jednym wektorem) należy je do siebie dodać. Dodawanie wektorów nie polega jednak na zsumowaniu ich wartości (gdyż jest to tylko jedna ich cecha), korzystamy natomiast z dwóch reguł dodawania geometrycznego:

• Reguła równoległoboku

Na pewne ciało działają dwa wektory (a i b). Przerysowujemy je, tak by powstał równoległobok (tworząc a' i b'). Na koniec tworzymy przekątną, rozpoczynającą się we wspólnym początku wektorów a i b, będącą ich wektorową sumą.

• Reguła trójkąta

Sytuacja jest podobna jak na pierwszym rysunku, jednak wektor b od razu przenosimy równolegle na koniec wektora a. Następnie dorysowujemy brakujący bok trójkąta, rozpoczynający się na początku wektora a i kończący się na końcu wektora b, będący wektorowa sumą a i b.

Niekiedy wektory trzeba od siebie odjąć (dodać z przeciwnym znakiem). Oto geometryczne wyjaśnienie jak to zrobić:

Aby zmienić znak wektora, należy zmienić jego zwrot (zastąpić początek wektora, końcem) - krok 2. Następnie zwyczajnie dodajemy powstałe wektory, w tym wypadku użyłem reguły trójkąta - krok 3.

Prostoliniowe dodawanie wektorów:

Pierwszy rysunek jest raczej oczywisty, wektor wypadkowy to suma długości wektora a i b. Na drugim rysunku, z kolei wektor a ma przeciwny zwrot niż wektor b, więc prostoliniowo odejmujemy od niego wektor a.Większość operacji na wektorach wykonuje się dużo prościej w układzie współrzędnych. W związku z tym, iż wektor to dwa punkty, jesteśmy w stanie go tam przenieść.

Jeszcze przed chwilą zajmowaliśmy się zsumowywaniem wektorów - liczeniem wypadkowej (daje nam to wyobrażenie np. jak w rzeczywistości poruszałby się jakiś obiekt). Czasem jednak musimy rozłożyć (zrzutować) wektor na kilka innych, np. jeśli jeden z rozłożonych wektorów siły powoduje ruch, zaś drugi jest równoważony (jest to klasyczny przykład ruchu po równi pochyłej, o tym w następnych lekcjach). Najczęściej wektor „rzutujemy” na oś OX i OY. Na rysunku powyżej tak właśnie zrzutowałem wektor a na składową x (a_x) i składową y (a_y). Dzięki tym operacjom stworzyliśmy dwa boki i przekątną prostokąta. Z wcześniejszych reguł wynika, iż wcale nie musi być to tylko i wyłącznie prostokąt; wektor możemy rozłożyć na więcej niż dwie składowe i pod innym kątem niż 90 stopni.

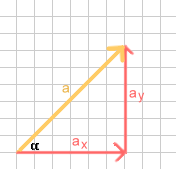
Co jeszcze daje nam rozłożenie na składowe? Gdy mamy dany wektor - są to przypominam tylko dwa punkty - i rozłożymy go na dwie składowe, możemy obliczyć np. kąt nachylenie go do osi OX. Wyobraźmy sobie rozłożony na składowe wektor a:

Stosunek jego składowych (tworzących trójkąt prostokątny) opisuje funkcja tangens kąta przy jednej składowej.

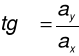
Gdy zaś mamy dane składowe, a chcemy obliczyć kąt zawarty między wektorem, a jedną z jego składowych, użyjmy funkcji odwrotnej:

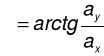
Znając składowe, możemy za pomocą funkcji trygonometrycznych lub twierdzenia pitagorasa obliczyć długość samego wektora:

Przytoczę raz jeszcze wzór na pracę - iloczyn siły i przesunięcia. Bystre oko zauważy pewną anomalię. Mnożymy wektor przez wektor, a praca przecież nie jest wektorem, tylko liczbą!

Otóż przytoczony wzór nie jest do końca poprawny; siła i przesunięcie to tzw.

iloczyn skalarny. Jest to rzut wektora a na wektor b:

Nie liczy się sama wartość siły i przesunięcia, lecz również kąt zawarty między nimi.

Dla przykładu, chcąc podnieść piłkę do góry, należy wektor siły ustawić pionowo, w każdym innym przypadku, droga do pokonania pewnej wysokości będzie większa, natomiast, gdy wektor siły ustawimy w stronę Ziemi, to ciało zacznie nie tyle się nie wznosić, co spadać. Kolejny przykład: gdy przesuwany teczkę w prawo, nigdy jej nie uniesiemy w górę (kąt pomiędzy siłą, a przesunięciem: 90 stopni).

Uogólnienie:

• Dla kątów większych od 0, ale mniejszych od 90 stopni, praca jest dodatnia, można rzecz, że „napędzamy ciało”.

• Dla kąta równego 90 stopni, praca jest równa 0, nie zmieniamy prędkości wzdłuż drogi.

• Dla kątów większych od 90 stopni, praca jest ujemna, jest to tak, jakbyśmy wyhamowywali ciało, prędkość wzdłuż pokonywanej drogi się zmniejsza.

Nie wspomniałem wcześniej o jeszcze jednej bardzo ważnej wielkości fizycznej: moment siły. Mimo, iż podobnie jak praca jest iloczynem dwóch wektorów, to moment siły też jest wektorem, którego cechy w dużej mierze zależą od kąta - jest to iloczyn wektorowy:

Długość (wartość) wektora przedstawia poniższy wzór:

Kierunek jest prostopadły do płaszczyzny na której leżą mnożone wektory, natomiast zwrot określa reguła prawej dłoni: wystawiamy kciuk prostopadle do pozostałych palców, które kierujemy od pierwszego wektora w iloczynie do drugiego (poprzez mniejszy z kątów utworzonych przez wektory). Kciuk prostopadły do płaszczyzny wskaże zwrot wektora.

Zasadę tą można w prosty sposób zrozumieć na sztandarowy przykładzie dźwigni (niech będzie dwustronna). Kąt między ramieniem a działającą siłą jest równy 90 stopni, więc wzór na wartość wektora nam się w znaczący sposób upraszcza (sin_90° = 1):

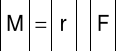
O iloczynie wektorowym możemy mówić jedynie w przestrzeni trójwymiarowej, z uwagi na prostopadły kierunek do płaszczyzny.

Wektory mają również ogromne znacznie w matematyce, rysowanie wykresów za pomocą translacji w dużej mierze ułatwia sprawę, w wykres jest czytelniejszy i bardziej profesjonalny; o tym w następnych lekcjach.

© Kamil Frydlewicz, 2008

Wektor przemieszczenia

Wektor prędkości

---