POLITECHNIKA WROCŁAWSKA INSTYTUT FIZYKI
|
SPRAWOZDANIE Z ĆWICZENIA NR 53
TEMAT : SPRAWDZANIE PRAWA OHMA DLA PRĄDU ZMIENNEGO.
|
ADAM R. WASILEWSKI
IZ rok II |
DATA WYKONANIA : 22 . 11 .95
OCENA : .............................. |
1. PRAWO OHMA.
Jeżeli do końcówek rezystora R przyłożymy napięcie stałe U, to natężenie prądu I płynącego przez rezystor jest proporcjonalne do przyłożonego napięcia.
; jest to znane prawo Ohma dla prądu stałego.
Jezeli do zacisków układu złożonego z szeregowo połączonych: rezystancji R, pojemności C i indukcyjności L przyłożymy SEM :
E = E0 sin ωt , gdzie E0 - amplituda SEM, to w układzie popłynie prąd sinusoidalnie zmienny o natężeniu I = I0 sin (ωt - ϕ), gdzie I0 - amplituda natężenia prądu,
ϕ - przesunięcie fazowe między natężeniem prądu a przyłożoną SEM;
Pomiędzy I0 i E0 zachodzi związek:
.
Zależność przedstawia prawo Ohma dla prądu zmiennego. Porównując wzory łatwo zauważyć, że rolę rezystancji w przypadku układu spełnia Z zwane impedancją.
Impedancję Z możemy obliczyć ze wzoru:
zaś przesunięcie fazowe ϕ ze wzoru:
Ponieważ w praktyce nie mierzy się amplitud I0 i E0, lecz wartości skuteczne Isk i Usk wygodniej jest prawo Ohma zapisac w postaci:
( na podstawie skryptu „Cwiczenia laboratoryjne z fizyki”)
2. POMIARY I OBLICZENIA.
2.1 Wartości początkowe i stałe:
Rl1 = (187 ± 1) Ω → δl1 = 0,53 %
Rl2 = (202 ± 1) Ω → δl2 = 0,50 %
Rl3 = (153 ± 1) Ω → δl3 = 0,65 %
2.2 Tabele pomiarowe:
Pomiar 1. ( C21)
|
R=450[Ω] |
|
|
|
R=225[Ω] |
|
|
|
L.P. |
U [V] |
I [mA] |
C [μF] |
ΔC [μF] |
U [V] |
I [mA] |
C [μF] |
ΔC [μF] |
|
|
|
|
|
|
|
|
|
1. |
5,4 |
9,0 |
8,02 |
0,59 |
5,4 |
13,5 |
9,62 |
0,99 |
2. |
7,5 |
13,5 |
9,77 |
1,16 |
7,4 |
16,5 |
8,20 |
0,43 |
3. |
10,9 |
18,5 |
8,37 |
0,24 |
9,8 |
22,5 |
8,54 |
0,09 |
4. |
13,4 |
22,5 |
8,16 |
0,45 |
12,9 |
30,5 |
8,89 |
0,26 |
5. |
16,6 |
28,5 |
8,61 |
0,00 |
16,0 |
37,5 |
8,78 |
0,15 |
6. |
19,6 |
33,7 |
8,64 |
0,03 |
19,8 |
41,5 |
7,57 |
1,06 |
7. |
23,5 |
40,5 |
8,69 |
0,08 |
23,0 |
54,0 |
8,80 |
0,17 |
|
|
|
|
|
|
|
|
|
średnia |
|
|
8,61 |
0,41 |
|
|
8,63 |
0,45 |
Pomiar 2. ( C22)
|
R=450[Ω] |
|
|
|
R=225[Ω] |
|
|
|
L.P. |
U [V] |
I [mA] |
C [μF] |
ΔC [μF] |
U [V] |
I [mA] |
C [μF] |
ΔC [μF] |
|
|
|
|
|
|
|
|
|
1. |
9,1 |
12,0 |
5,21 |
0,27 |
6,0 |
9,5 |
5,39 |
0,09 |
2. |
10,9 |
14,5 |
5,29 |
0,19 |
9,2 |
14,5 |
5,37 |
0,11 |
3. |
13,9 |
18,5 |
5,29 |
0,19 |
13,0 |
20,7 |
5,43 |
0,05 |
4. |
16,2 |
23,0 |
5,87 |
0,39 |
16,4 |
26,5 |
5,42 |
0,06 |
5. |
19,2 |
26,2 |
5,61 |
0,13 |
18,5 |
30,5 |
5,65 |
0,17 |
6. |
20,8 |
28,5 |
5,54 |
0,06 |
20,4 |
33,4 |
5,60 |
0,12 |
7. |
23,7 |
32,5 |
5,55 |
0,07 |
23,1 |
36,8 |
5,43 |
0,05 |
|
|
|
|
|
|
|
|
|
średnia |
|
|
5,48 |
0,19 |
|
|
5,48 |
0,09 |
Pomiar 3. ( C23)
|
R=450[Ω] |
|
|
|
R=225[Ω] |
|
|
|
L.P. |
U [V] |
I [mA] |
C [μF] |
ΔC [μF] |
U [V] |
I [mA] |
C [μF] |
ΔC [μF] |
|
|
|
|
|
|
|
|
|
1. |
6,6 |
10,8 |
7,70 |
0,01 |
5,3 |
11,2 |
7,65 |
0,32 |
2. |
9,0 |
14,5 |
7,45 |
0,24 |
8,8 |
18,8 |
7,75 |
0,22 |
3. |
11,8 |
19,0 |
7,44 |
0,25 |
11,9 |
26,0 |
7,99 |
0,02 |
4. |
14,4 |
23,5 |
7,65 |
0,04 |
15,0 |
33,5 |
8,22 |
0,25 |
5. |
17,4 |
29,0 |
8,02 |
0,33 |
17,4 |
38,2 |
8,04 |
0,07 |
6. |
20,4 |
33,7 |
7,86 |
0,17 |
20,0 |
44,0 |
8,06 |
0,09 |
7. |
23,5 |
38,5 |
7,72 |
0,03 |
23,0 |
50,6 |
8,06 |
0,09 |
|
|
|
|
|
|
|
|
|
średnia |
|
|
7,69 |
0,15 |
|
|
7,97 |
0,15 |
Przykładowe obliczenia:
Do dalszych obliczeń przyjmujemy:
C21 = (8,62 ± 0,46) μF
C22 = (5,48 ± 0,19) μF
C23 = (7,83 ± 0,30) μF → gdyż jest to jedyna możliwość połączenia obu (stosunkowo
różnych) wyników;
Pomiar 4. (L1)
|
R=450[Ω] |
|
|
|
R=225[Ω] |
|
|
|
L.P. |
U [V] |
I [mA] |
L [H] |
ΔL [H] |
U [V] |
I [mA] |
L [H] |
ΔL [H] |
|
|
|
|
|
|
|
|
|
1. |
6,9 |
10,0 |
0,84 |
0,08 |
5,0 |
10,5 |
0,76 |
0,02 |
2. |
9,7 |
14,0 |
0,87 |
0,11 |
8,4 |
17,8 |
0,73 |
0,01 |
3. |
14,5 |
21,0 |
0,85 |
0,09 |
10,9 |
23,2 |
0,72 |
0,02 |
4. |
17,8 |
26,5 |
0,68 |
0,08 |
15,3 |
32,5 |
0,73 |
0,01 |
5. |
19,5 |
29,0 |
0,69 |
0,07 |
18,6 |
39,2 |
0.75 |
0,01 |
6. |
21,5 |
32,0 |
0,68 |
0,08 |
20,9 |
43,8 |
0,77 |
0,03 |
7. |
24,0 |
35,7 |
0,68 |
0,08 |
24,2 |
51,0 |
0,75 |
0,01 |
|
|
|
|
|
|
|
|
|
średnia |
|
|
0,76 |
0,08 |
|
|
0,74 |
0,02 |
Pomiar 5. ( L2)
|
R=450[Ω] |
|
|
|
R=225[Ω] |
|
|
|
L.P. |
U [V] |
I [mA] |
L [H] |
ΔL [H] |
U [V] |
I [mA] |
L [H] |
ΔL [H] |
|
|
|
|
|
|
|
|
|
1. |
7,0 |
9,8 |
0,93 |
0,02 |
5,6 |
10,7 |
0,96 |
0,02 |
2. |
9,5 |
13,1 |
1,01 |
0,06 |
8,2 |
15,6 |
0,98 |
0,04 |
3. |
12,0 |
16,5 |
1,03 |
0,08 |
10,3 |
20,0 |
0,92 |
0,02 |
4. |
15,0 |
20,9 |
0,95 |
0,00 |
13,9 |
27,0 |
0,92 |
0,02 |
5. |
18,5 |
26,0 |
0,91 |
0,04 |
18,2 |
35,1 |
0,94 |
0,00 |
6. |
21,0 |
29,5 |
0,91 |
0,04 |
21,4 |
41,2 |
0,94 |
0,00 |
7. |
23,5 |
33,0 |
0,91 |
0,04 |
24,6 |
47,5 |
0,93 |
0,01 |
|
|
|
|
|
|
|
|
|
średnia |
|
|
0,95 |
0,04 |
|
|
0,94 |
0,01 |
Pomiar 6. ( L3)
|
R=450[Ω] |
|
|
|
R=225[Ω] |
|
|
|
L.P. |
U [V] |
I [mA] |
L [H] |
ΔL [H] |
U [V] |
I [mA] |
L [H] |
ΔL [H] |
|
|
|
|
|
|
|
|
|
1. |
7,6 |
10,8 |
1,15 |
0,04 |
6,2 |
11,8 |
1,16 |
0,02 |
2. |
9,8 |
13,5 |
1,29 |
0,10 |
9,3 |
17,1 |
1,24 |
0,06 |
3. |
13,0 |
18,0 |
1,27 |
0,08 |
11,3 |
21,2 |
1,20 |
0,02 |
4. |
16,0 |
22,4 |
1,22 |
0,03 |
14,4 |
27,8 |
1,13 |
0,05 |
5. |
19,0 |
27,0 |
1,15 |
0,04 |
18,2 |
34,7 |
1,16 |
0,02 |
6. |
21,5 |
30,7 |
1,13 |
0,06 |
21,9 |
41,5 |
1,17 |
0,01 |
7. |
24,0 |
34,3 |
1,13 |
0,06 |
24,1 |
45,8 |
1,17 |
0,01 |
|
|
|
|
|
|
|
|
|
średnia |
|
|
1,19 |
0,06 |
|
|
1,18 |
0,03 |
Przykładowe obliczenia:
ΔL = 0.08326 + 0.00083 + 0.00770 + 0.00077 = 0,09256 [H]
Do dalszych obliczeń przyjmujemy:
L1 = (0,76 ± 0,08) H
L2 = (0,95 ± 0,04) H
L3 = (1,19 ± 0,06) H
Pomiar 7. (C21, L1)
R = 225 [Ω]
L.P. |
U [V] |
I [mA] |
Z [Ω] |
ΔZ [Ω] |
|
|
|
|
|
1. |
5,0 |
11,4 |
438,60 |
4,79 |
2. |
7,0 |
16,0 |
437,50 |
3,69 |
3. |
9,0 |
20,5 |
439,02 |
5,21 |
4. |
11,0 |
25,3 |
434,78 |
0,97 |
5. |
13,0 |
30,0 |
433,33 |
0,48 |
6. |
15,0 |
34,9 |
429,80 |
4,01 |
7. |
17,0 |
39,5 |
430,38 |
3,43 |
8. |
19,0 |
44,0 |
431,82 |
1,99 |
9. |
21,0 |
48,5 |
432,99 |
0,82 |
10. |
23,0 |
53,5 |
429,91 |
3,90 |
|
|
|
|
|
średnio |
|
|
433,81 |
2,93 |
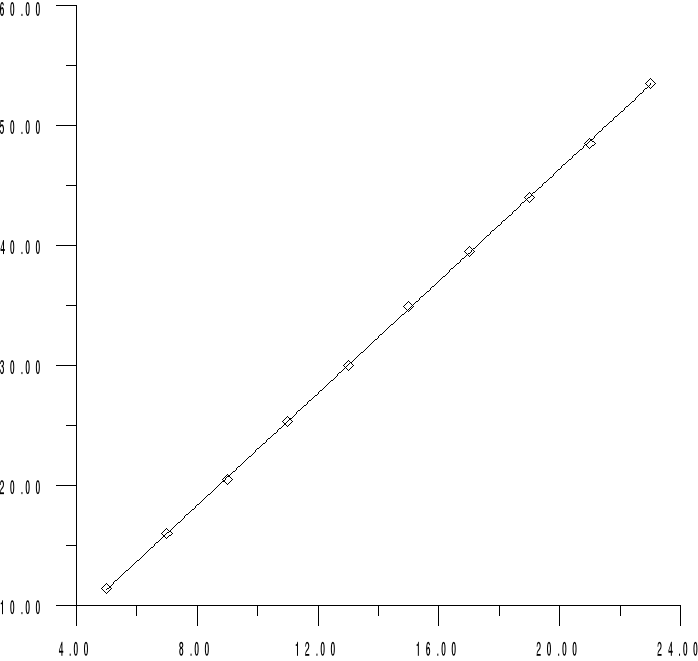
Impedancja obliczona na podstawie zmierzonych wcześniej wartości L i C :
ΔZ = 0.9999 + 0.0999 = 1.0998 [Ω]
Pomiar 8. (C22, L2)
R = 275 [Ω]
L.P. |
U [V] |
I [mA] |
Z [Ω] |
ΔZ [Ω] |
|
|
|
|
|
1. |
5,5 |
10,2 |
539,22 |
12,77 |
2. |
7,8 |
14,0 |
557,14 |
5,15 |
3. |
10,0 |
17,9 |
558,66 |
6,67 |
4. |
12,0 |
21,3 |
563,80 |
11,81 |
5. |
14,0 |
25,5 |
549,02 |
2,97 |
6. |
16,0 |
29,2 |
547,95 |
4,04 |
7. |
18,0 |
32,8 |
548,78 |
3,21 |
8. |
20,0 |
36,5 |
547,95 |
4,04 |
9. |
22,0 |
39,5 |
556,96 |
4,97 |
10. |
24,0 |
43,6 |
550,46 |
1,53 |
|
|
|
|
|
średnio |
|
|
551,99 |
5,72 |
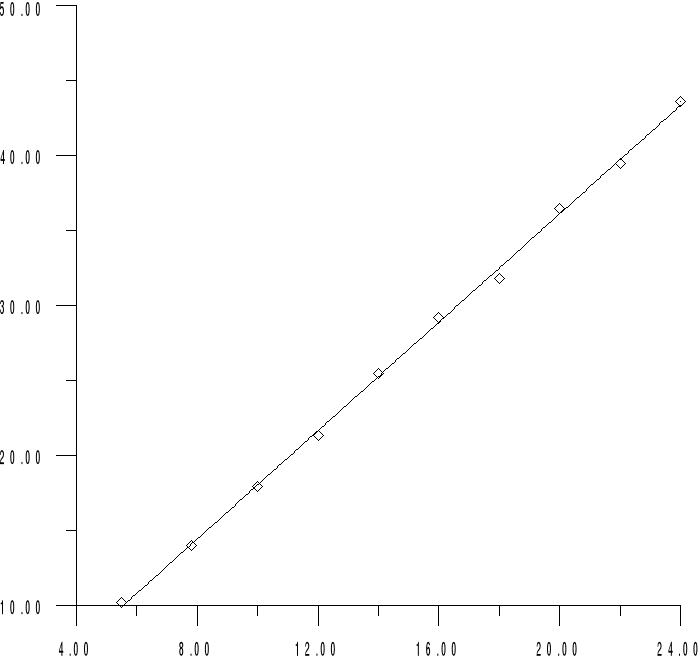
Impedancja obliczona na podstawie zmierzonych wcześniej wartości L i C :
ΔZ = 0.99994 + 0.09999 = 1.09993 [Ω]
Pomiar 9. (C23, L3)
R = 550 [Ω]
L.P. |
U [V] |
I [mA] |
Z [Ω] |
ΔZ [Ω] |
|
|
|
|
|
1. |
6,8 |
10,0 |
680,00 |
31,72 |
2. |
9,0 |
12,5 |
720,00 |
8,28 |
3. |
11,0 |
15,0 |
733,33 |
21,61 |
4. |
13,0 |
17,7 |
734,46 |
22,74 |
5. |
15,0 |
20,7 |
724,64 |
12,92 |
6. |
17,0 |
23,5 |
723,40 |
11,68 |
7. |
19,0 |
26,8 |
708,96 |
2,76 |
8. |
21,0 |
29,9 |
702,34 |
9,38 |
9. |
22,5 |
32,4 |
694,44 |
17,28 |
10. |
24,0 |
34,5 |
695,65 |
16,07 |
|
|
|
|
|
średnio |
|
|
711.72 |
15,44 |
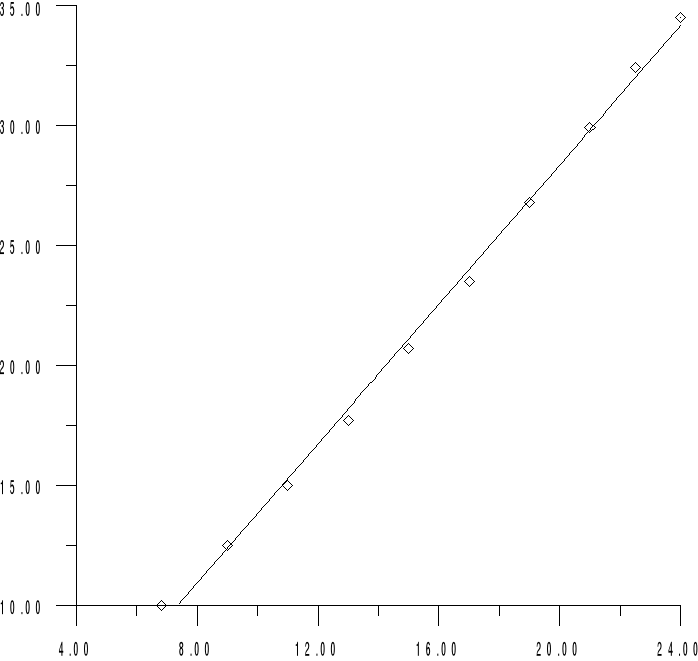
uwaga:
Na powyższych wykresach na osi X odkładaliśmy wartości napięcia U, na osi Y wartości pradu (w [mA]).
Impedancja obliczona na podstawie zmierzonych wcześniej wartości L i C :
ΔZ = 0.099 + 0.990 = 1.089 [Ω]
UWAGA:
Wartości impedancji można wyznaczyć z wykresu, uwzględniając fakt, iz impedancja równa jest co do wartości tangesowi nachylenia prostej tworzącej wykres I=f(U).
3. WNIOSKI
Analizując otrzymane wyniki można stwierdzić prawdziwość wzoru na prawo Ohma dla prądu zmiennego. Przy pomiarze pojemności kondenstatorów w zasadzie wyniki dla różnych wartości rezystancji były podobne (trochę z tej zasady wyłamał się pomiar trzeci), z czego można wnioskowac, iż błędy przypadkowe tych pomiarów nie były duże. Podobny wniosek można wysnuć uwzględniając błąd pomiaru wyliczony na podstawie różniczki zupełnej.
W przypadku pomiaru indukcyjności cewek. Tutaj juz obyło się bez wyjątków od zupełnie przyzwoitych wartości odchyłek. Również błąd wyliczony przy pomocy różniczki zupełnej mieści się w granicach tolerancji.
Na podstawie powyzszych uwag można stwierdzić, że otrzymalismy dobre podstawy do zasadniczej części ćwiczenia - sprawdzania prawa Ohma.
Przed dokonaniem pomiarów intrugujące było pytanie jak bardzo różnić się będą wyniki wyliczone ze zmierzonych wartości U i I od tych wyznaczonych z parametrów RLC.
Po dokonaniu analizy okazało się, że wyniki te różniły się w niewielikim stopniu, co świadczy o sporej dokładności przeprowadzenia ćwiczenia. Gwoli ścisłości pragnę zaznaczyć, że patrząc na wykres można zauważyć niewielkie odchyłki od prostej, co również potwierdza powyższą tezę.
Wyszukiwarka