Zadania powtórzeniowe- zjazd I

-------------------------------------------------------------------------

1.Rozwiązać układ nierówności. Zilustrować graficznie otrzymany wynik:

a).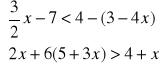
b).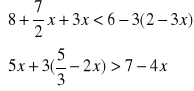

c).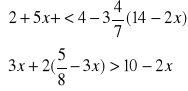
d).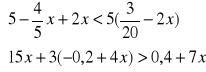

2. Naszkicować wykres podanej funkcji oraz wskazać zbiór argumentów, dla których funkcja ta jest dodatnia (jej wartościami są liczby dodatnie):

a).
b).
c).
d).

e).
f).
g).

h).

3. Zilustrować na płaszczyźnie zbiór punktów (x,y) należących do zbioru:

a).

b).

c).

d).

e).

f).

g).

h).

4. Wykorzystując wyniki zadania (3) zaznaczyć wskazane zbiory:

5). Rozwiązać nierówność:

a).
b).
c).
d).

6. Przeanalizować wartość logiczną zdania:

a).
b).
c).
d).

e).
f).
g).
h).

7). Podać sąsiedztwo i otoczenie punktu x₀ o promieniu r :

a). x₀ =3; r =1 b). x₀ = 0,2; r = 0,3 c). x₀ = -6; r =0,1 d). x₀ =-π; r =0,4

Zaznaczyć odpowiednie zbiory na osi liczbowej.

8). Naszkicować wykresy funkcji

a).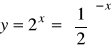
b).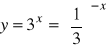
c).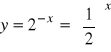
d).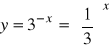

9). Rozwiązać nierówności:

a).
b).
c).
d).

10).

a). Dana jest funkcja kwadratowa y=f(x), znaleźć zbiór tych argumentów , dla których funkcja osiada wartości dodatnie. Zilustrować wynik graficznie

b). Dana jest funkcja kwadratowa y=f(x), znaleźć zbiór tych argumentów , dla których funkcja osiada wartości ujemne. Zilustrować wynik graficznie

c). Dana jest funkcja kwadratowa y=f(x), znaleźć zbiór tych argumentów , dla których funkcja osiada wartości dodatnie. Zilustrować wynik graficznie

d). Dana jest funkcja kwadratowa y=f(x), znaleźć zbiór tych argumentów , dla których funkcja osiada wartości ujemne. Zilustrować wynik graficznie

e). Dana jest funkcja kwadratowa y=f(x), znaleźć zbiór tych argumentów , dla których funkcja osiada wartości dodatnie. Zilustrować wynik graficznie

f). Dana jest funkcja kwadratowa y=f(x), znaleźć zbiór tych argumentów , dla których funkcja osiada wartości ujemne. Zilustrować wynik graficznie

---