WOJSKOWA AKADEMIA TECHNICZNA

--------------------------------------------------------------------------------------------------------

LABORATORIUM FIZYCZNE

Grupa szkoleniowa C04J mgr inż. Leszek Kubiak
stopień i nazwisko

prowadzącego

GOLONKA Marcin

( imię i nazwisko słuchacza)

ocena końcowa ocena przygot.

do ćwiczenia

SPRAWOZDANIE

Z

PRACY LABORATORYJNEJ Nr 18

Temat: Wyznaczanie przerwy energetycznej germanu.

1. Wstęp teoretyczny.

Ciała stałe ze względu na ich właściwości elektryczne dzielimy na trzy grupy:

1) przewodniki, w których stany zapełnione sąsiadują bezpośrednio ze stanami pustymi (np. metale);

2) izolatory, w których najmniejsza energetyczna odległość między stanami zapełnionymi elektronami i pustymi zwana przerwę energetyczną (E_g ) jest duża tzn. większa niż 2eV (np. dla diamentu wynosi ona 5,4eV);

3) półprzewodniki, w których przerwa energetyczna jest mniejsza niż 2 eV ( np. dla krzemu wynosi 1,1eV);

Aby elektron uczestniczył w przewodnictwie prądu elektrycznego musi pobierać energię od przyłożonego z zewnątrz pola elektrycznego, a to jest możliwe tylko wówczas, gdy znajdują się one w paśmie przewodnictwa. Elektrony takie nazywamy swobodnymi, gdyż mogą poruszać się po całym krysztale. Wydajność opisanego termicznego procesu wzbudzania elektronów do pasma przewodnictwa bardzo silnie zależy od wartości przerwy energetycznej:

-przy jej praktycznym braku (przewodniki) już w temperaturze kilkudziesięciu kelwinów wszystkie elektrony biorą udział w przewodnictwie;

-gdy jest ona bardzo duża (w izolatorach) nawet w temperaturach rzędu kilkuset stopni Celsjusza elektronów swobodnych w ciele stałym jest tak mało, że praktycznie nie przewodzi on prądu;

-natomiast w półprzewodnikach gdzie przerwa energetyczna jest mniejsza już w temperaturze pokojowej część elektronów jest przeniesiona do pasma przewodnictwa, co umożliwia przepływ prądu. Ogrzewanie półprzewodnika wymusza generacją elektronów swobodnych, co powoduje silny wzrost przewodnictwa.

Wielkością elektryczną określającą ilość nośników ładunku jest ich koncentracja. Koncentracją swobodnych elektronów (n) nazywamy liczbę elektronów w paśmie przewodnictwa przypadającą na jednostkę objętości ciała, koncentracją dziur (p) nazywamy liczbę dziur w paśmie walencyjnym w jednostce objętości ciała. Koncentracje nośników rosną wykładniczo z temperaturą (T):

p = n = 2(2π kT / h²)^3/2 (m_n m_p)^3/4 exp -(E_g/2kT)

k - stała Boltzmanna

h - stała Plancka

m_n , m_p - masy efektywne dla elektronu i dziury w danym półprzewodniku

W praktyce stosuje się wzór:

p = n = n₀ exp -(E_g/2kT), gdzie n₀ traktuje się jako stałą niezależną od temperatury

Gęstość prądu w półprzewodnikach dana jest wzorem:

j = e (n v_n + p v_p)

j - gęstość prądu ;

e - ładunek elektronu;

v_p , v_n - średnie prędkości elektronów i dziur

Wprowadzając pojęcie ruchliwości nośników zdefiniowanej wzorami:

μ_n = v_n/E, μ_p = v_p/E

j = e(n μ_n + p μ_p)E, gdzie E - natężenie przyłożonego pola elektrycznego

Porównując ostatni wzór z prawa Ohma:

j = σE

otrzymujemy wzór na przewodnictwo półprzewodników :

σ = e

W ćwiczeniu wyznaczamy przerwę energetyczną germanu z pomiarów zależności rezystancji półprzewodnika samoistnego od temperatury. Zależność tę możemy zapisać:

R=R₀exp[E_g/2kT].

Logarytmując obustronnie otrzymujemy:

log R = log R₀ + 0,4343 Eg/2k 1/T.

a więc zależność log R = f(1/T) jest prostą, a jej nachylenie wynosi 0,4343Eg/2k.

2. Wyniki pomiarów.

T[K]	R[ohm]	Prąd[A]
293		0,5
298	1217
303	995
308	783
313	614
318	483
323	386	0,7
328	321
333	262
338	213
343	176	0,9
348	150
353	126
358	106
363	90
368	77
373	66	1,1
378	58
383	51
388	45
393	39

3. Obliczenia

Posługując się metodą najmniejszych kwadratów Gaussa obliczam stałe a i b, sprowadzając w ten sposób zależność log R = f(1/T) do postaci y = ax + b, oraz wyznaczam odchylenie standardowe σ_a. W tym celu korzystam ze wzorów: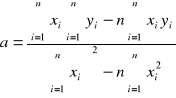
,


,
.

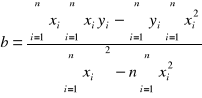
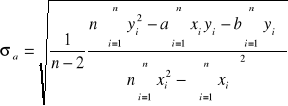
Znając a i σ_a obliczam Eg i σ_Eg ze wzorów:
,
.

Dla poziomu ufności p = 0,95 obliczam przedział ufności ∆Eg ze wzoru:
.

Do powyższych obliczeń skorzystałem z pomocy programu Excel.

log10[R] = y			1/T = x		Xi*Yi		x^2		y^2
			0,00341
	3,09		0,00336		0,010353		1,13E-05		9,52
	3		0,0033		0,009894		1,09E-05		8,99
	2,89		0,00325		0,009395		1,05E-05		8,37
	2,79		0,00319		0,008908		1,02E-05		7,77
	2,68		0,00314		0,00844		9,89E-06		7,2
	2,59		0,0031		0,008008		9,59E-06		6,69
	2,51		0,00305		0,007642		9,3E-06		6,28
	2,42		0,003		0,007262		9,02E-06		5,85
	2,33		0,00296		0,006889		8,75E-06		5,42
	2,25		0,00292		0,006547		8,5E-06		5,04
	2,18		0,00287		0,006253		8,26E-06		4,74
	2,1		0,00283		0,00595		8,03E-06		4,41
	2,03		0,00279		0,005657		7,8E-06		4,1
	1,95		0,00275		0,005384		7,59E-06		3,82
	1,89		0,00272		0,005126		7,38E-06		3,56
	1,82		0,00268		0,004878		7,19E-06		3,31
	1,76		0,00265		0,004665		7E-06		3,11
	1,71		0,00261		0,004458		6,82E-06		2,92
	1,65		0,00258		0,004261		6,64E-06		2,73
	1,59		0,00254		0,004049		6,47E-06		2,53
Suma y	45,2	Suma x	0,0583	SumaXi*Yi	0,134019	Suma x^2	0,000171	Suma(y^2)	106
		(Suma x)^2	0,0034	n*SumaXi*Yi	2,680385	n*suma	0,003422	n*suma	2127
			a	1859,970999		suma(EPSi^2)	0,002672
			b	-3,16080189		sigma a	11,10694
			Błąd wzgl. a	0,005971568
						Eg[J]	11820,22
						Eg[eV]	0,737841
						sigma Eg[J]	70,58523
						sigma Eg [eV]	0,004406
						poziom uf.	0,95
						Delta Eg	0,008636

Stąd przerwa energetyczna germanu wynosi Eg = 11820,22 [J], odchylenie standardowe σ_Eg = 70,58 [J] oraz przedział ufności ∆Eg = 0,0086 [eV].

4. Wnioski

Wykres logR =f (1/T) przedstawia zależność logarytmu rezystancji półprzewodnika od odwrotności temperatury. Ma ona w przybliżeniu charakter liniowy. Wartość błędu względnego wyznaczenia współczynnika kierunkowego tej prostej wynosi 0,6%, a zatem jest on wyznaczony z dużą dokładnością.

Celem doświadczenia było wyznaczenie przerwy energetycznej germanu. Wynik, jaki otrzymaliśmy w doświadczeniu to 0,738+/-0,004 eV. Wartość Eg rzeczywista wynosi 0,67 eV dla temperatury 293K, zatem otrzymany wynik nie mieści się w dopuszczalnej granicy błędu.

W doświadczeniu mogły wystąpić pewne błędy, które spowodowały rozbieżności pomiędzy otrzymany wynikiem, a wartością rzeczywistą. Ich źródłem mogły być:

- niedokładność w wyznaczaniu rezystancji próbki,

- niedokładność w wyznaczaniu temperatury,

- różnica pomiędzy temperaturą panującą w laboratorium,

---