Temat: Badanie zjawiska dyfrakcji i interferencji światła laserowego

Celem ćwiczenia jest:

• pomiar szerokości szczeliny oraz odległości między szczelinami

• wyznaczanie stałej siatki dyfrakcyjnej

• wyznaczenie długości fali lasera półprzewodnikowego

Opis przyrządu

Ćwiczenie było wykonywane przy pomocy przyrządu składającego się z lasera gazowego i półprzewodnikowego, układu zwierciadeł, szczelin dyfrakcyjnych lub siatki oraz przyrządu do rejestrowania natężenia światła na matówce.

CZĘŚĆ I

(wyznaczenie szerokości szczeliny dla 1 szczeliny)

a = 0,08 mm

L = 193 cm ΔL = 0,5 cm

= 10 s/cm

Nr pomiaru	Rząd dyfrakcji	Położenie kursora tl [ms]	Położenie kursora tp [ms]
I	1 2	98430 84971	125668 138486
II	1 2	102477 89025	124100 142926
III	1 2	104531 91079	131529 144652

Dla każdego t_l i t_p wyznaczamy położenie minimum x_m ze wzoru

Nr pomiaru	Rząd dyfrakcji	Minimum xm [10^-5 m]
I	1 2	1361,90 2675,75
II	1 2	1081,15 2695,05
III	1 2	1349,90 2678,65

Dla każdego rzędu dyfrakcji obliczamy średnią wartość x_m, odchylenie
i niepewność Δx_m rozszerzoną współczynnikiem Studenta-Fishera (w naszym przypadku
).

obliczamy ze wzoru:
, gdzie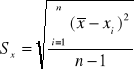
; gdzie
jest wartością średnią, a n liczbą pomiarów równą 3.

Rząd dyfrakcji	Średnia wartość xm [10^-5 m]	[10^-5 m]	Δxm [10^-5 m]
1	1264,32	91,65	394,34
2	2683,15	62,53	269,05

Dla każdego m obliczamy szerokość szczeliny ze wzoru:
dla λ = 632,8 nm

Rząd dyfrakcji	Szerokość szczeliny a [10^-6 m]
1	96,60
2	91,06

Rachunek jednostek:

Wynik końcowy będzie, wiec średnia wyników cząstkowych

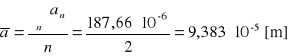
Δa_i obliczamy metodą różniczki zupełnej ze wzoru: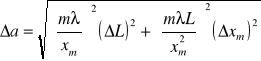

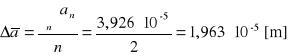
Wnioski:

CZĘŚĆ II

(wyznaczanie odległości między szczelinami i szerokości każdej z nich)

a = 0,04 mm

d = 0,25 mm

L = 193,2 cm, ΔL = 0,5 cm

= 10 s/cm

Nr pomiaru	Rząd dyfrakcji	Położenie kursora tl [ms]	Położenie kursora tp [ms]
I	1	90520	141806
II	1	93135	144140
III	1	93136	144702

Nr pomiaru	Ilość prążków N	Położenie kursora tl [ms]	Położenie kursora tp [ms]
I	20	70062	167028
II	20	72116	168270
III	20	72491	169364

Wyznaczamy Δx_i między dwoma minimami interferencyjnymi ze wzoru:

Nr pomiaru	Δxi [10^-5 m]
I	484,83
II	485,77
III	484,37

Następnie obliczamy wartość średnią x, odchylenie
i niepewność Δx ze wzorów takich jak wyżej.

Δx = 484,99 · 10^-5 m

= 0,41 · 10^-5 m

ΔΔx = 1,77 · 10^-5 m

Odległość między szczelinami:

Odległość między szczelinami obliczamy ze wzoru:
dla λ = 632,8 nm i L = 193,2 cm

Rachunek jednostek jest następujący:

Błąd pomiaru Δd obliczamy metodą różniczki zupełnej:

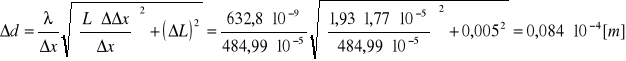
Szerokość szczelin:

Obliczamy x_mi dla każdego pomiaru ze wzoru

Nr pomiaru	xmi [10^-5 m]
I	2564,30
II	2550,25
III	2578,30

Wartość średnia: x = 2564,28 · 10^-5 m;
= 8,11 · 10^-5 m; Δx = 34,85 · 10^-5 m

Obliczamy szerokość szczeliny ze wzoru:
dla λ = 632,8 nm i m = 1

Błąd Δa wyznaczamy metodą różniczki zupełnej jak w części I:

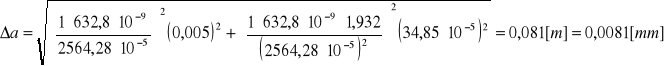
Wnioski:

Wnioski z części I i II:

CZĘŚĆ III

(wyznaczenie stałej siatki dyfrakcyjnej)

L = 60,5 cm ΔL = 0,5 cm

Nr pomiaru	Rząd dyfrakcji	Położenie kursora tl [ms]	Położenie kursora tp [ms]
I	2 1	4671 47642	181041 135827
II	2 1	5605 48390	181788 136014
III	2 1	5792 94137	182788 136762

Dla każdego x_mi wyznaczamy położenie m-tego maksimum dyfrakcyjnego ze wzoru:

Nr pomiaru	Rząd dyfrakcji	Maksimum xm [10^-5 m]
I	2 1	8818,50 4409,25
II	2 1	8809,15 4381,20
III	2 1	8849,80 4381,25

Dla każdego rzędu dyfrakcji obliczamy wartość średnią x_m, odchylenie
i niepewność pomiarową Δx_m rozszerzoną współczynnikiem Studenta-Fishera (w naszym przypadku
).

obliczamy ze wzoru:
, gdzie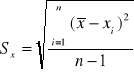
; gdzie
jest wartością średnią, a n liczbą pomiarów równą 3.

Rząd dyfrakcji	Średnia wartość xm [10^-5 m]	[10^-5 m]	Δxm [10^-5 m]
1	4390,57	9,34	40,19
2	8825,82	12,35	53,14

Stałą siatki można wyznaczyć ze wzoru: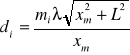

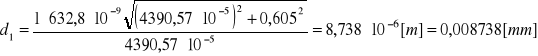
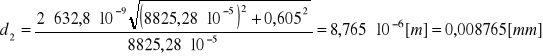
Błąd Δd_i wyznaczamy metodą różniczki zupełnej: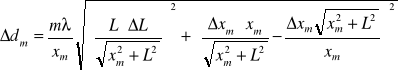

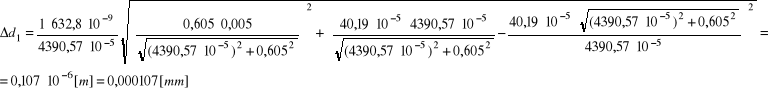
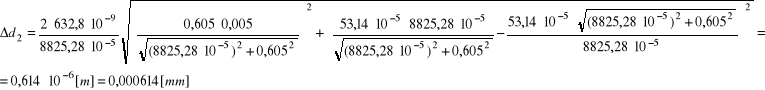
d_śr = 0,008755 mm; Δ d_śr = 0,000761 mm

Skoro posiadamy już stałą siatki możemy obliczyć ilość linii przypadającą na 1 mm siatki. Ilość ta wyraża się wzorem:

CZĘŚĆ IV

(wyznaczenie długości fali lasera półprzewodnikowego)

L = 60,5 cm ΔL = 0,5 cm

Nr pomiaru	Rząd dyfrakcji	Położenie kursora tl [ms]	Położenie kursora tp [ms]
I	2 1	10649 56797	201032 150400
II	2 1	10836 56984	200285 1540400
III	2 1	10836 56797	195537 150027

Dla każdego x_mi wyznaczamy położenie m-tego maksimum dyfrakcyjnego ze wzoru:

Nr pomiaru	Rząd dyfrakcji	Maksimum xm [10^-5 m]
I	2 1	9519,15 4680,15
II	2 1	9472,45 4670,80
III	2 1	9235,05 4661,50

Dla każdego rzędu dyfrakcji obliczamy wartość średnią x_m, odchylenie
i niepewność pomiarową Δx_m rozszerzoną współczynnikiem Studenta-Fishera (w naszym przypadku
).

obliczamy ze wzoru:
, gdzie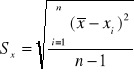
; gdzie
jest wartością średnią, a n liczbą pomiarów równą 3.

Rząd dyfrakcji	Średnia wartość xm [10^-5 m]	[10^-5 m]	Δxm [10^-5 m]
1	4670,82	5,38	23,15
2	9408,88	87,96	378,47

Aby obliczyć długość fali należy skorzystać ze wzoru: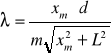
.

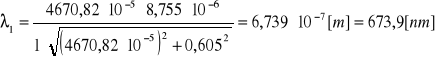
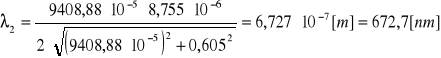
Błąd Δλ obliczamy metodą różniczki zupełnej ze wzoru: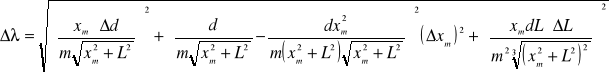

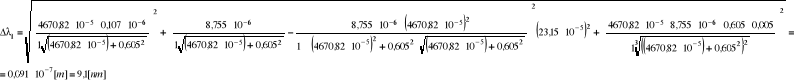
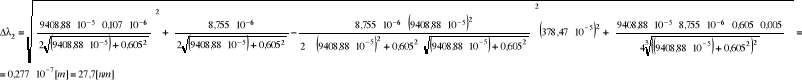
λ = 673,3 nm

Δλ = 18,4 nm

Wnioski:

rejestrator

szczelina lub układ szczelin lub siatka dyfrakcyjna

zwierciadło

Laser He-Ne lub półprzewodnikowy

---