NAZWISKO:PIOTROWSKI IMIE:ŁUKASZ KIERUNEK:FIZYKA Z INFORMATYKĄ ROK STUDIÓW: II GRUPA LABORATORYJNA: XIII		WYŻSZA SZKOŁA PEDAGOGICZNA W RZESZOWIE I PRACOWNIA FIZYCZNA
				WYKONANO		ODDANO
				DATA	PODPIS	DATA	PODPIS
Ćwiczenie Nr: 72b	Temat: Wyznaczanie promienia krzywizny soczewek metodą odbicia.

Część teoretyczna

Wyznaczanie promienia krzywizny soczewek metodą odbicia

Wypolerowana powierzchnia kulista soczewki ma włściwości zwierciadła sferycznego, bo częściowo odbija padające na nią promieniowanie. Na tej właściwości soczewek oparta jest metoda pomiaru promienia krzywizny ich powierzchni.Metodę tę moża stosować w przypadku soczewek o stosunkowo długich ogniskowych. Jeśi przed soczewką np. wklęsło-wypukłą , umieśimy przedmiot o długości L tak że znajdzie się on przed powierzchnią wypukłą, to zauważmy, żę utworzą się dwa obrazy przedmiotu, bowiem obie powierzchnie soczewki działją jak zwierciadła

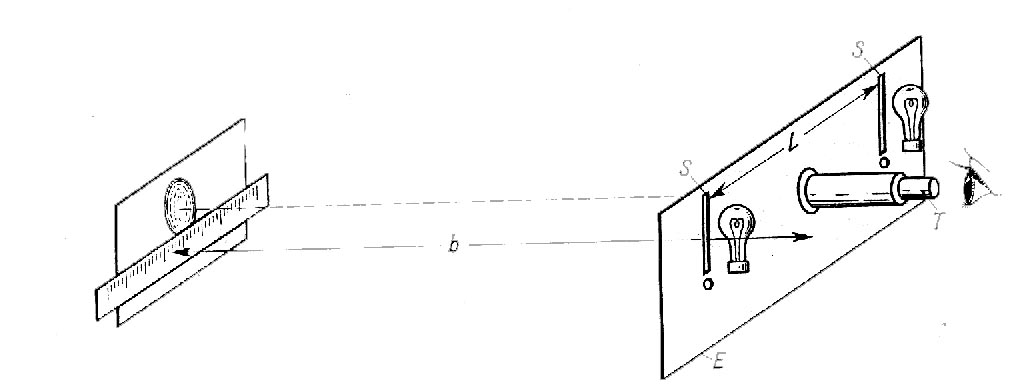
Soczewkę umieszczamy w podstawce p w odległści b od nieprzeźroczystego
ekranu E, w którym wycięte są dwie szczelinki S odległe od siebie o L. Szczelinki te odgrywają rolę krańców przedmiotu o długości L. Obrazy obserwujemy za pomocą lunety T. Szczelinki S są oświetlone od drugiej strony żarówkami. Obserwują przez lunetę soczewkę wklęsoł-wypukłą zobaczymy oczywiśice dwa obrazy przedmiotu czyli cztery szczelinki. Obydwa obrazy są proste, ale luneta odwraca je, tak że olądane przez nią wydają się odwrócone. Uwzglęniamy tylko obraz utworzony przez odbicie od powierzchni znajdująej się bezpośednio przed szczelinami (przed ekranem E), ponieważ na ten obraz

składa się wyłącznie zjawisko odbicia, podczasgdy obraz dawany przez drugą powierzchnię jest wynikiem zjawiska odbicia i załamania promieni. Ten drugi obraz moża odróżnićdzięki mniejszej jasności obrazów szczelinek S, co jest spowodowane stratą światła przy dwóh dodatkowych odbiciach. Wielko-
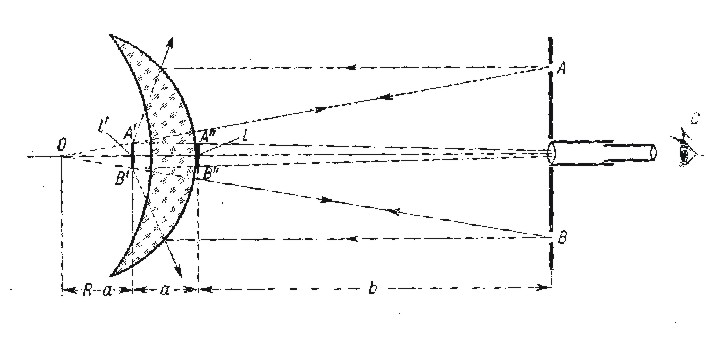
śi obrazu l' (zaznaczonego jako A'B' na rysunku ) nie możemy mierzyć bezpośrednio, natomiast mierzymy jego rzut rónoległy l za pomocą linijki przyłożonej stycznie do powierzchni soczewki. Zaznaczyć należ, że odcinek A"B" jest tylko w przybliżniu rzutem rónoległm A'B'. Jednak ze wzglęu na dużą odległść soczewki od ekranu można przyjąć l' = l. Otrzymane trzy wielkośi:

b - odległość przedmiotu od soczewki

L - wielkoś przedmiotu (AB) i

l- wielkość rzutu obrazu l'
posłużą do wyprowadzenia wzoru na promień krzywizny powierzchni wypukłej. Odległość obrazu l' od przedniej powierzchni soczewki niech będzie a. Na podstawie zależności między wielkośicą obrazu i przedmiotu a odległśicą obrazu i przedmiotu od zwierciadła mamy:

l'/L=a/b (1)

a = l'b/L (2)

z podobieństwa trójkątów OA'B' i OAB

l'/L=(R-a)/(R+b)

po podstawieniu wartości a otrzymujemy

l'/L = (RL-l'b)/L(R+b) (3)

i stąd

R=2bl'/(L-l') (4)

Z podobieństwa trójkątów A'B'C i A”B”C

l'/l = (b + a)/b

po podstawieniu (2)

l'/l= (bL+l'b)/bL

oraz

l'=lL/(L-l) (5)

podstawiając (5) do (4) mamy

R = 2blL(L-l)/(L - l)[L(L - l) - Ll] = 2bl/(L - 2l)

---