Pochodna funkcji
![]()
![]()
![]()
![]()
![]()
Różniczkowa wartość funkcji
Niech funkcja ![]()
będzie określona w pewnym otoczeniu Q punktu x0, w którym jest różniczkowalna. Dowolny ( różny od zera ) przyrost ![]()
zmiennej niezależnej x oznaczamy symbolem dx i nazywamy różniczką zmiennej niezależnej.
Różniczką dy funkcji f(x) w punkcie x0 i dla przyrostu dx nazywamy iloczyn
![]()
Pochodna ( interpretacja geometryczna )
![]()
Pochodna - granica ilorazu różnicowego. Tangens konta pomiędzy styczną
do wykresu funkcji w punkcie x0, f(x0) z osią OX
Styczna - graniczne położenie siecznej
![]()
![]()
![]()
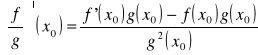
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Twierdzenie o pochodnej superpozycji
![]()
![]()
- złożona
Pochodna funkcji odwrotnej
![]()
![]()
![]()
![]()
![]()
![]()
![]()
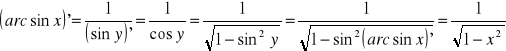
y = arc tg x
x = tg y
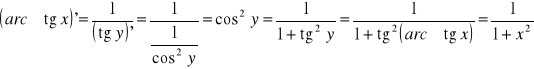
![]()
![]()
![]()
Materiały na zaliczenie - Piszczała - Wykłady z analizy matematycznej”, analiza matematyczna - skrypt
Twierdzenia:
Twierdzenie Lagrange ( o przyrostach )
![]()
- ciągła
![]()
![]()
styczna równoległa do siecznej
![]()
![]()
jest rosnąca
Monotoniczność funkcji
Funkcję f nazywamy monotoniczną w zbiorze A, jeżeli jest funkcją niemalejącą lub nierosnącą w zbiorze A
Funkcję f nazywamy ściśle monotoniczną w zbiorze A, jeżeli jest funkcją rosnącą lub malejącą w zbiorze A
Funkcję f nazywamy rosnącą w X, jeżeli ![]()
Funkcję f nazywamy niemalejącą w X, jeżeli ![]()
Funkcję f nazywamy malejącą w X, jeżeli ![]()
Funkcję f nazywamy nierosnącą w X, jeżeli ![]()
Ekstrema funkcji ( lokalne )
Mówimy, że funkcja f, określona w otoczeniu x = x0, ma w tym punkcie maksimum ( lokalne ), jeżeli istnieje otoczenie (x0 - h, x0 + h ) tego punktu takie, że dla każdego x ∈ (x0 - h, x0 + h ) jest f(x) < f(x0)
Mówimy, że funkcja f, określona w otoczeniu x = x0, ma w tym punkcie minimum
( lokalne ), jeżeli istnieje otoczenie (x0 - h, x0 + h ) tego punktu takie, że dla każdego x ∈ (x0 - h, x0 + h ) jest f(x) > f(x0)
Mówimy, że funkcja f, określona w otoczeniu x = x0, ma w punkcie x0 ekstremum ( lokalne ), jeżeli ma w tym punkcie maksimum lub minimum
( lokalne )
Wypukłość i wklęsłość funkcji
|
|
wypukła |
wklęsła |
)
(
x0
pochodna funkcji
α
dy
Δy
dx
styczna
dy
dx
= tg ∝
f(x0)
x0+dx
x0
x
y
f(x0+dx)
f(x)
f(x0)
x0
x
f(x) - f(x0)
x - x0
Z różniczkowalności funkcji w punkcie wynika jej ciągłość w tym punkcie
f(x) = |x|
∝
Jeżeli funkcja jest różniczkowalna w punkcie x0, ma w tym punkcie ekstremum lokalne, to f'(x)=0
Jeżeli funkcja posiada ekstremum i pochodną
w jednym punkcie - pochodna jest równa 0