POLITECHNIKA WROCŁAWSKA INSTYTUT METROLOGII ELEKTRYCZNEJ
Krzysztof Najdzionek	Sprawozdanie z ćwiczenia nr 2. Temat: Pomiary pośrednie.
Wydział Elektroniki Rok I	Data: 01,04,1998	Ocena:

Wykaz przyrządów użytych w ćwiczeniu:

• Multimetr cyfrowy LG

• Woltomierz analogowy LM-3

• Miliamperomierz analogowy LM-3

• Rezystor dekadowy

0. Pomiar bezpośredni oporności omomierzem cyfrowym.

1. Schemat układu pomiarowego:

2. Wyniki pomiarów:

	Rn/P	Rx
L.p.	/W	
1	20/2	20,07
2	200/0,5	197,64
3	20k/0,5	19,352 k

1. Pomiar rezystancji metodą pośrednią.

1. Obliczenie maksymalnego napięcia i prądu.

	Rn	Umax	Imax
L.p.		V	A
1	20	6,32	0,32
2	200	10,00	0,05
3	20k	100,00	0,005

2. Dobór przyrządów pomiarowych.

Polecenie: woltomierz, miliamperomierz - typ LM-3.

3. Układ poprawnie mierzonego prądu.

1. Schemat układu pomiarowego.

2. Wyniki pomiarów.

	U	Uz	±U	I	Iz	±I	R	Rp	±R	±δR
L.p.	V	V	V	mA	mA	mA				
1	3,00	3	0,02	148,50	150	0,75	20,20	20,04	0,16	0,79
2	5,00	7,5	0,04	23,00	30	0,15	217,39	216,62	0,77	0,36
3	20,00	30	0,15	1,03	3	0,02	19417,48	19409,81	7,67	0,04

3. Przykładowe obliczenia.

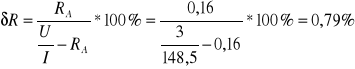
4. Układ poprawnego pomiaru napięcia.

1. 
   Schemat układu pomiarowego.

2. Wyniki pomiarów

	U	± U	Uz	I	± I	Iz	R	Rp	±  R	±δR
L.p.	V	V	V	mA	mA	mA				%
1	3,00	0,02	3	150,00	0,75	150	20,00	20,13	0,13	0,67
2	5,00	0,04	7,5	25,00	0,15	30	200,00	205,48	5,48	2,67
3	20,00	0,15	30	1,7	0,02	3	11764,71	19354,84	7590,13	39,22

3. Przykładowe obliczenia.

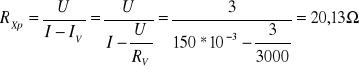
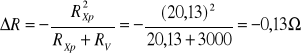
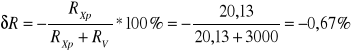
2. Pomiar rezystancji metodą porównania spadku napięć.

1. 
   Schemat układu pomiarowego.

2. Wyniki pomiarów

	URx	±URx	URn	± URn	RN	±RN	RX	±RX	±δRX
L.p.	V	V	V	V					%
1	1,4471	0,0018	1,4194	0,0018	20	0,1	20,39	0,15	0,75
2	5,015	0,009	5,088	0,009	200	1	197,13	1,69	0,86
3	10,014	0,014	5,173	0,009	10000	50	19358,21	157,53	0,81

3. Przykładowe obliczenia.

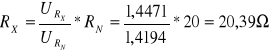
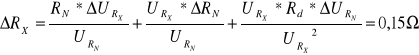
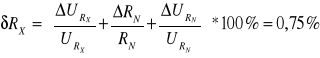
3. Pomiar rezystancji wewnętrznej woltomierza analogowego LM -3.

1. 
   Schemat układu pomiarowego.

2. Wyniki pomiarów.

	UV	±UV	RN	±RN	RV	±RV	±δRV
L.p.	V	V					%
1	7,50	0,04	0	0	-
2	7,00	0,04	470	2,35	6580,00	1123,30	32,50
3	6,00	0,04	1869	9,345	7476,00	485,94	4,06
4	5,00	0,04	3732	18,66	7464,00	335,88	1,78
5	4,00	0,04	6564	32,82	7501,71	283,99	1,15

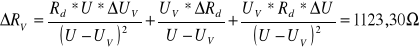
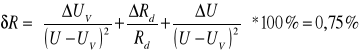
4. Wnioski.

Celem ćwiczenia było poznanie metod pośrednich pomiaru różnych wielkości fizycznych. Jako pierwsze badaliśmy rezystory. Wartość ich rezystancji można wyznaczyć przez pomiar natężenia prądu i spadku napięcia na nim, lub przez porównanie wartości spadku napięcia na rezystorze badanym oraz na rezystorze o znanej wartości. Ponieważ nie można na raz mierzyć napięcia i prądu płynącego przez rezystor korzystając z metody pomiaru prądu i napięcia możemy zastosować jeden z dwóch układów - z poprawnie mierzonym napięciem lub prądem. Pierwszy z nich przeznaczony jest do pomiaru małych wartości rezystancji, drugi zaś do pomiaru dużych wartości rezystancji. Sposób ich użycia wyznacza błąd metody (w tabelkach ujęty jako R i δR) wyznaczany ze wzorów podanych powyżej. W układzie z poprawnie mierzonym napięciem mierzymy sumę prądów płynących przez rezystor oraz przez woltomierz. Dla rezystancji zbliżonych wartością (lub większych) do rezystancji wejściowej woltomierza prąd płynący przez miernik stanowi coraz większą część mierzonego natężenia, dla równych wartości obu rezystancji stanowi on już połowę mierzonej wartości. Podobnie jest dla drugiego układu, z tym, że zamiast prąd mamy doczynienia z napięciem. Mierzymy w tym układzie sumę spadków napięć na rezystorze oraz na miliamperomierzu - rezystor z rezystancją wewnętrzną amperomierza tworzy dzielnik napięcia, im mniejsza jest wartość rezystora, tym większa część napięcia odkłada się na mierniku, a nie na elemencie badanym. Stosując obie te metody można wyeliminować z nich błąd dołączając do wartości otrzymanej z obliczeń poprawkę obliczoną z błędu metody. Głównymi czynnikami wprowadzającymi błąd do pomiaru są rezystancje wewnętrzne wykorzystywanych mierników. Doboru metody można dokonać w oparciu o wzór
, gdy wartość R_X=R_G to w obu metodach wystąpi błąd metody o jednakowej wartości, dla R_X<R_G stosujemy układ poprawnie mierzonego napięcia, w przeciwnym wypadku należy zastosować układ poprawnie mierzonego prądu. Innym sposobem pomiaru nieznanej rezystancji jest porównanie spadków napięć na rezystancji badanej i na innej o znanej wartości. Ponieważ w obwodzie płynie stały prąd, możemy wyznaczyć wartość badanej rezystancji. Jest to metoda dokładniejsza od metody pomiaru napięcia i prądu, a najważniejsze można ją stosować do wszystkich wartości rezystorów. Jej dokładność zależy głównie od dokładności rezystora o znanej wartości, ponieważ stosunek pomiaru napięć eliminuje błąd systematyczny pomiaru woltomierzem ( oba wskazania obarczone są tym samym błędem, więc ich stosunek jest zawsze stały i nie zależy od błędu miernika). Nie występuje tu błąd metody. Podobnie jest w przypadku ostatniej części ćwiczenia - pomiaru rezystancji wewnętrznej woltomierza analogowego - nie występuje błąd metody, zaś dokładność zależy głównie od klasy użytego rezystora dekadowego oraz w mniejszym stopniu od dokładności mierzenia napięcia.(niema tu jednak możliwości wyeliminowania błędu systematycznego). Dokładniejszy jest pomiar dla danej wartości dekady względem napięcia przy rezystancji dekady równej zero - od błędu odejmuje się jeden człon zależny od błędu dokładności dekady - dla wartości zero jest on równy zero. Wykonane pomiary pozwalają uzmysłowić zakresy stosowalności poznanych metod pomiarowych ( w wielu przypadkach nie można zastąpić metody pośredniej pomiaru metodą bezpośrednią tzn. odczytem ze skali miernika wyskalowanego w jednostkach wartości mierzonej z określoną dokładnością na ogół większą niż przy pomiarach laboratoryjnych) oraz ich wady wynikające z doboru sprzętu pomiarowego.



R_x

R_N

V

A

R_x

V

V

R_x

R_N

V

A

R_x

---