Temat: Wyznaczanie współczynnika rozszerzalności liniowej ciał stałych

Wstęp teoretyczny

Podczas zmianiy temperatury ciała ulegają także zmianie jego wymiary liniowe. Elementarny przyrost temperatury, powoduje przyrost długości określony poniższym wzorem:

.

Gdzie: α-nazywamy współczynnikiem rozszerzalności liniowej, l-dł. danego ciała

Współczynnik rozszerzalności liniowej zależy od rodzaju ciała a także od jego temperatury. Ponieważ α zależy od temperatury, więc długość ciała (l) jest on na ogół nieliniową funkcją temperatury. Przy niewielkich zmianach temperatury możemy przyjąć że współczynnik α w przybliżeniu jest wartością stałą (tzw. średni współczynnik rozszerzalności liniowej). Możemy więc skorzystać z następującego wzoru:

.

Zjawisko rozszerzalności cieplnej polega na tym, że dostarczając ciału energię w postaci ciepła wprowadzamy atomy tego ciała w drgania o dużej częstotliwości. Amplituda tych drgań rośnie wraz ze wzrostem temperatury, rośnie także ich średnia wzajemna odległość, co makroskopowo objawia się jako rozszerzalność cieplna.

Schemat doświadczenia

• Mierzymy długość początkową prętów

• Odczytujemy temperaturę początkową

• Podgrzewamy wodę przepływającą przez pręty

• Odczytujemy długość prętów co 5⁰C

• Wykonujemy wykres zależności wydłużenia od temp.

• Obliczamy wartości współczynnika rozszerzalności cieplnej dla każdego przyrostu temperatury, oraz wartość średnią.

• Obliczamy odchylenie standardowe średniej.

Pomiary i obliczenia:

Tabela pomiarowa:

Nr pomiaru	Temperatura [^oC]	Długość-ogrzewanie [mm]		Długość- stygniecie [mm]
				Stal	Mosiądz	Stal	Mosiądz
Dane początkowe	20	788,6	788,6	788,6	788,6
1	25	788,67	788,74	788,64	788,68
2	30	788,71	788,84	788,69	788,76
3	35	788,76	788,93	788,73	788,84
4	40	788,81	788,98	788,79	789,92
5	45	788,86	789,08	788,84	789,01
6	50	788,91	789,18	788,89	789,09
7	55	788,96	789,25	788,94	789,17
8	60	789,01	789,34	788,99	789,25
9	65	789,06	789,43	789,04	789,33
10	70	789,11	789,51	789,09	789,44

Wartości współczynnika rozszerzalności cieplnej obliczamy ze wzoru na przyrost długości:

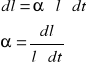
a więc otrzymujemy:

dl		dt	α
Stal	Mosiądz		Stal	Mosiądz
0,07	0,08	5	1,77514E-05	2,02881E-05
0,06	0,1	5	1,52147E-05	2,53585E-05
0,05	0,09	5	1,26781E-05	2,28215E-05
0,05	0,05	5	1,26773E-05	1,26776E-05
0,05	0,1	5	1,26765E-05	2,53537E-05
0,05	0,1	5	1,26757E-05	2,53521E-05
0,05	0,07	5	1,26749E-05	1,77453E-05
0,05	0,09	5	1,26741E-05	2,2814E-05
0,05	0,09	5	1,26733E-05	2,28125E-05
0,05	0,08	5	1,26725E-05	2,02765E-05

Dyskusja błędów:

t = ±1 [⁰C]

Δl = ± 0,01 [mm]

Obliczamy odchylenie standardowe współczynnika rozszerzalności liniowej z następującego wzoru:

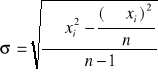
gdzie: x_i = α

Obliczamy również średnią arytmetyczną obliczonych współczynników rozszerzalności liniowej korzystając z poniższego wzoru:

Odchylenie standardowe wynosi:

Dla mosiądzu: 0,126783 ·10^-05

Dla stali: 0,0541802 ·10^-05

Średni współczynnik rozszerzalności liniowej wynosi:

Dla mosiądzu: 2,15493 ·10^-05

Dla stali: 1,34364 ·10^-05

Ostateczne wyniki:

Dla mosiądzu: 2,15 ± 0,13 ·10^-05

Dla stali: 1,34 ± 0,05 ·10^-05

Przykład obliczeń:

Obliczam współczynnik rozszerzalności liniowej dla pierwszego pomiaru, dla stali:

Wnioski:

Jak łatwo możemy zauważyć z wykresów długość pręta wzrasta proporcjonalnie do temperatury. Współczynnik rozszerzalności liniowej stali oraz mosiądzu obliczyłem dla ogrzewania, nie obliczałem dla chłodzenia, ponieważ przy chłodzeniu nie ulega on zmianie. Błędy powstałe przy pomiarach spowodowane są niedokładnością przyrządów pomiarowych.

Wykres współczynnika rozszerzalności liniowej ciał stałych

---