1. Zasada równoległoboku (zasada pierwsza)

Działanie dwóch sił P₁ i P₂ można zastąpić działaniem jednej siły R, działającej na ten sam punkt, będącej przekątną równoległoboku ABCD zbudowanego na wektorach sił P₁ i P₂.

Wypadkową R wyznaczamy ze wzoru:         


W przypadku, gdy siły P₁ i P₂ działają wzdłuż jednej prostej i są zgodnie skierowane, wartość wypadkowej wynosi:          


Natomiast, gdy siły są przeciwnie skierowane i P₂ =P₁ , to      
    

2. Układ zerowy

Skutek działania dowolnego układu sił przyłożonego do ciała nie zmieni się, jeśli do tego układu dodamy lub odejmiemy dowolny układ równoważących się sił, czyli tzw. układ zerowy. Wynika stąd następujący wniosek: każdą siłę działającą na ciało sztywne można przesunąć dowolnie wzdłuż jej linii działania.

3. Zasada zesztywnienia

Jeżeli ciało odkształcalne znajduje się w równowadze pod działaniem pewnego układu sił, to również pozostanie w równowadze ciało doskonale sztywne (nieodkształcalne), identyczne z poprzednim, pod działaniem tego samego układu sił. Wynika stąd wniosek, że warunek konieczny i wystarczający do równowagi ciała sztywnego jest tylko warunkiem koniecznym, ale nie wystarczającym do równowagi ciała odkształcalnego.

4. Zasada działania i przeciwdziała

Każdemu działaniu towarzyszy równe co do wartości, o przeciwnym zwrocie i leżące na tej samej prostej przeciwdziałanie.

5. Zasada oswobodzenia od więzów

Każde ciało nieswobodne można myślowo oswobodzić z więzów, zastępując ich działanie reakcjami, a następnie rozważać jako ciało swobodne znajdujące się pod działaniem sił czynnych i biernych (reakcji więzów).

6.Więzy

Więzami nazywamy warunki ograniczające ruch ciała w przestrzeni. Wprowadzenie więzów jest równoznaczne z działaniem na ciało sił biernych, czyli reakcji. Więzy w których nie występuje tarcie nazywamy więzami bez tarcia albo więzami idealnymi.

Przypadki więzów:

- Przegub walcowy

Ciało sztywne jest osadzone na walcowym sworzniu przechodzącym przez kołowy otwór wykonany w tym ciele. Po pominięciu siły tarcia jako małej w porównaniu z siłą normalną R do powierzchni styku linia działania tej reakcji będzie przechodziła przez oś sworznia. Występujące dwie reakcje R_x i R_y stanowią dwie niewiadome i umożliwiają wyznaczenie wartości reakcji R i jej kierunku.

- Przegub kulisty

W celu unieruchomienia punktu podparcia w przestrzeni stosuje się przeguby kuliste, które krępują swobodę przesunięć, ale umożliwiają obrót wokół dowolnej osi. Ich zakończenie jest wykonane w kształcie kuli, która jest osadzona w łożysku kulistym. W wyniku pominięcia sił tarcia w przegubie kulistym powstaje reakcja R o dowolnym kierunku w przestrzeni, przechodząca przez środek kuli i mająca trzy niezależne składowe R_x, R_y i R_z.

- Podpora przegubowa przesuwna (rolkowa).
Ponieważ opór przy przesuwaniu takiej podpory w kierunku poziomym jest bardzo mały, przyjmuje się, że linia działania reakcji jest prostopadła do płaszczyzny poziomej (przesuwu).

- Podpora przegubowa stała.

W przypadku zastosowania podpory przegubowej stałej koniec podparcia ciała sztywnego może się obracać dookoła osi przegubu, ale nie może się przemieszczać w dwóch kierunkach. Przy założeniu, że w przegubie nie ma tarcia, linia działania reakcji R przechodzi przez punkt A. Powstają dwie niezależne od siebie składowe reakcje R_x iR_y. Rozważając podporę przegubową stałą w przestrzeni należy zauważyć, że koniec podparcia B nie może się przemieszczać w trzech kierunkach i dlatego występują trzy niezależne składowe reakcje R_x, R_y iR_z.

- Zawieszenie na cięgnach wiotkich.              
Podwieszenie ciała za pomocą wiotkich cięgien stwarza tzw. podpory kierunkowe jednostronne, bo cięgna mogą być tylko rozciągane. Reakcje S₁ i S₂ działają na ciało wzdłuż tych cięgien, zgodnie z rysunkiem.

- Oparcie o gładką i chropowatą powierzchnię.
W przypadku oparcia ciała o gładką powierzchnię (styk punktowy) występuje jedna reakcja R_A, prostopadła do powierzchni styku. Jeżeli powierzchnia będzie chropowata, to wystąpią dwie składowe reakcji R_A: normalna do powierzchni N i styczna siła tarcia T.

- Utwierdzenie całkowite.
Gdy chodzi o zupełne unieruchomienie ciała, wtedy stosuje się utwierdzenie całkowite. Ciało sztywne na płaszczyźnie ma trzy stopnie swobody, a więc wystąpi reakcja R o dwóch składowych R_x i R_y oraz moment utwierdzenia M. Rozważając całkowite unieruchomienie ciała w przestrzeni, należy zastosować takie utwierdzenie, które przedstawia sześć więzów. Wystąpi wtedy reakcja R o trzech składowych R_x, R_y i R_z oraz moment utwierdzenia M o trzech składowych M_x, M_y i M_z .

- Ciało podparte na prętach zamocowanych przegubowo na obu końcach (prętach przegubowych).
Ciało sztywne można także unieruchomić przez podparcie na prętach zakończonych przegubami. Jeżeli pominiemy ciężary własne prętów i tarcie w przegubach, to reakcje na ciało będą działać wzdłuż tych prętów S_A, S_B i S_C , zgodnie z rysunkiem.

7. Moment siły względem osi

Momentem siły względem osi jest miara obrotowego działania siły względem tej osi. Jest on równy rzutowi na tę oś momentu danej siły względem dowolnego punktu leżącego na tej osi

8. Moment siły względem prostej

Momentem siły F wzg. prostej l nazywamy moment rzutni siły F na dowolna płaszczyznę prostopadłą do prostej wzg. Punktu przebicia tej płaszczyzny przez prosta l .

9. Układ statycznie wyznaczalny i niewyznaczalny

Układ statycznie wyznaczalny:

Układami statycznie wyznaczalnymi nazywamy takie zagadnienia, które dotyczą równowagi układu sił działających w jednej płaszczyźnie na jedno lub kilka ciał sztywnych (układ mechaniczny), w których istnieje możliwość wyznaczenia niewiadomych sił. Niewiadome siły stanowią zwykle reakcje podpór albo siły wzajemnego oddziaływania wewnątrz rozważanego układu mechanicznego. W przypadku układu statycznie wyznaczalnego liczba reakcji zastępujących działanie więzów jest równa liczbie równań równowagi. Jeżeli więzów jest za mało, to dany układ mechaniczny jest niesztywny. Równowaga takiego układu może być zapewniona w przypadku spełnienia dodatkowych warunków, które zapewniają układowi odpowiednią postać geometryczną.

Układ statycznie niewyznaczalny:

Gdy więzów jest więcej niż potrzeba do unieruchomienia danego układu mechanicznego, dany układ jest przesztywniony. Wówczas niewiadomych reakcji jest więcej niż mamy równań równowagi i dlatego niektórych reakcji nie można wyznaczyć metodami stosowanymi w statyce. Zagadnienia takie nazywamy układami statycznie niewyznaczalnymi.

BELKI:

Belki statycznie wyznaczalne są to belki, dla których liczba niewiadomych podporowych jest równa liczbie równań równowagi.

Metodyka rozwiązywania belek statycznie wyznaczalnych:
1. Wyznaczenie wartości reakcji podpór pisząc trzy równania równowagi
2. Wyznaczenie momentów gnących w miejscach przyłożenia sił skupionych
3. Obliczenie sił tnących w poszczególnych przedziałach belki
4. Przyjęcie podziałki dla momentów gnących i sił tnących
5. Sporządzenie wykresów momentów gnących i sił tnących z zachowaniem znaków.

Przykłady belek statycznie wyznaczalnych:

Belki statycznie niewyznaczalne są to belki, w których liczba niewiadomych jest większa od liczby równań równowagi.

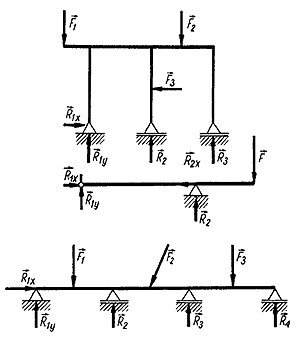
Niektóre metody rozwiązywania układów statycznie niewyznaczalnych:
1. Metoda sił
2. Metoda przemieszczeń
3. Metoda superpozycji
4. Metoda trzech momentów
5. Metoda Menabrei

Przykłady takich belek to: belki wieloprzęsłowe (o trzech lub więcej podporach), belki dwustronnie utwierdzone, belki jednym końcem utwierdzone, a na drugim podparte etc.

            

10. Tarcie poślizgowe

Tarciem nazywa się zjawisko powstawania sił stycznych do powierzchni styku dwóch ciał.
T. poślizgowe-ciało leżące na poziomej pow. zacznie się po niej ślizgać, gdy przyłoży się do niego siłę F, która musi przekroczyć pewną wartość graniczną. Wtedy T=μN(współ. t. pośli. normalny);T- nie zależy od wielkości styku; μ-zależy od materiałów stykających i pow.

1. W przypadku ciała pozostającego w spoczynku na chropowatej powierzchni zależność między siłą tarcia T a naciskiem normalnym N wyraża się następująco

     
             gdzie μ współczynnik tarcia ślizgowego (statycznego).

2. W przypadku ciała ślizgającego się po chropowatej powierzchni siła tarcia jest skierowana przeciwnie do kierunku ruchu, a jej wartość jest określona zależnością

           
gdzie μ_k współczynnik tarcia ślizgowego (kinetycznego).

11. Moment siły F względem punktu 0

Momentem sił wzg. punktu 0 nazywamy wektor Mo(F) związany z punktem 0 prostopadłym do płaszczyzny określonej przez siłę F1 i punkt 0.

12.Przedmiot materialny.

Punktem materialnym nazywamy ciało o wymiarach znikomo małych w porównaniu z rozmiarami obszaru, w którym się porusza tak, że można pominąć zmiany położenia tego ciała wywołane przez obrót. Traktuje się to ciało jako punkt geometryczny, w którym jest skupiona skończona ilość materii, czyli obdarzony pewną masą.

13. Ciało doskonale sztywne.

Ciało doskonale sztywne (nieodkształcalne), czyli takie wyidealizowane ciało stałe, którego punkty nie zmieniają wzajemnych odległości pod wpływem działających na nie sił.

14. Statyka

Zajmuje się równowagą ciał materialnych poddanych działaniu sił, zadanie-ustalenie warunków równowagi sił.

15. Siła

Siła jest miarą wzajemnego oddziaływania ciał, przejawiającego się wyprowadzeniem ich ze stanu spoczynku, zmianą ich ruchu lub utrzymaniem ciał wstanie równowagi. Jednostką siły w układzie międzynarodowym SI jest niuton (1 N).

16. Rodzaje sił

Siłami zewnętrznymi nazywamy siły, które zastępują działanie sił oddziałujących na rozpatrywane ciało, przy izolowaniu tego ciała od innych, pierwotnie z nim połączonych. Występują one jako tzw. siły czynne obciążające ciało i jako reakcje więzów, tzw. siły bierne.

Siły wewnętrzne stanowią oddziaływania między poszczególnymi elementami ciała. Na podstawie piątej zasady statyki siły wewnętrzne są zawsze parami przeciwne, mają równe wartości i działają wzdłuż tej samej prostej. W celu ujawnienia tych sił stosuje się metodę przecięć, która polega na myślowym przecięciu ciała dowolną płaszczyzną.

Siły Masowe -proporcjonalne do masy ciała, mają charakter grawitacyjny oraz bezwładnościowy

Siły kontaktowe- punktowe, liniowe, powierzchniowe.

17. Para sił

Para sił - układ dwóch sił równoległych o równych wartościach, przeciwnych zwrotach; nie ma wypadkowej; wywołuje obrót ciała sztywnego

18. Układ sił.

Układy sił, w których linie działania przecinają się w jednym punkcie nazywamy zbieżnymi układami sił. Takie układy mogą być płaskie lub przestrzenne.

Przestrzenny układ sił zbieżnych P₁, P₂,..., P_n przyłożonych do punktu O można zastąpić siłą wypadkową P równą sumie geometrycznej tych sił i przyłożoną również w punkcie O

                  

Dowolny układ sił działających na ciało sztywne zastąpić można siłą R przyłożoną do dowolnego środka redukcji O, równą sumie geometrycznej wszystkich sił układu, oraz para sił o momencie Mo, równym sumie geometrycznej momentów tych sił względem ośrodka O.

19. Tarcie toczne.

Tarcie toczenia powstaje przy usiłowaniu przetoczenia walca o ciężarze G po poziomej płaszczyźnie.

Siła tarcia tocznego musi spełniać warunki (przy równowadze walca)

                 
    

W przypadku toczenia walca wartość siły tarcia tocznego T musi być mniejsza od wartości siły tarcia ślizgowego nie rozwiniętego co wyraża się nierównością

                 
gdzie f - współczynnik tarcia tocznego, r - promień walca.

 Tarciem cięgna o krążek nazywamy siły tarcia występujące między powierzchniami cylindrycznymi i cięgnami na nie nawiniętymi. Związek miedzy napięciami S₁ i S₂  w cięgnie opasującym krążek wyraża się wzorem

      

           
gdzie μ współczynnik tarcia ślizgowego (statycznego) między cięgnem a powierzchnią krążka, alfa kąt opasania, na którym cięgno przylega do krążka.

20. Wytrzymałość materiałów

Wytrzymałość materiałów jest nauką o trwałości spotykanych w praktyce typowych elementów konstrukcji, poddanych działaniu obciążenia zewnętrznego (sił i momentów). Jej podstawą są prawa i zasady mechaniki ogólnej, w której badane ciała są rozpatrywane jako elementy sztywne.
Wytrzymałość materiałów uwzględnia zdolność ciał stałych do odkształcania  i zajmuje się badaniem oraz ustalaniem zależności odkształceń od sił zewnętrznych, działających na rozpatrywane elementy konstrukcyjne. Zatem jest nauką stosowaną, zajmującą się badaniem zjawisk występujących w ciałach odkształcalnych. Podstawą wytrzymałości materiałów są obliczenia teoretyczne i badania doświadczalne.

21. Prawo Hooke'a

Δl = P⋅l/E⋅F; Wydłużenie Δl pręta pryzmatycznego jest wprost proporcjonalne do siły rozciągającej P i do dług. początkowej l pręta, odwrotnie proporcjonalne do pola F przekroju poprzecznego .E-moduł Younga [Pa]

Prawo Hooke'a dla ścinania

22. Wydłużenie względne

ε=Δl/l - wydłużenie względne (doznaje jednostka długości .pręta), gdzie Δl - całkowite wydłużenie (skrócenie), l - długość początkowa

23. Wykres sił rozciągania

T -tau czyli naprężenie

24. Umocnienie plastyczne

Podwyższenie własności wytrzymałościowych materiału, wynikające z wywołania w próbce odkształceń trwałych. 

25. Naprężenie dopuszczalne.
 

Naprężenia, które mogą występować w materiale bez obawy naruszenia warunku wytrzymałości i warunku sztywności, nazywamy naprężeniami dopuszczalnymi.
Oznaczamy je literą k z odpowiednim indeksem dolnym, charakteryzującym rodzaj odkształcenia:
      k_r - naprężenie dopuszczalne przy rozciąganiu,
      k_c - naprężenie dopuszczalne przy ściskaniu,
      k_g - naprężenie dopuszczalne przy zginaniu,
      k_t - naprężenie dopuszczalne przy ścinaniu,
      k_s - naprężenie dopuszczalne przy skręcaniu.

Liczbę n oznaczającą, ile razy naprężenie dopuszczalne jest mniejsze od granicy wytrzymałości (dla materiałów kruchych) lub od granicy plastyczności (dla materiałów plastycznych), nazywa się współczynnikiem bezpieczeństwa.

W przypadku rozciągania materiałów kruchych       
           

Dla materiałów plastycznych                  


gdzie: R_m - granica wytrzymałości na rozciąganie, otrzymana w wyniku prób wytrzymałościowych, R_e - granica plastyczności.

26. Zasada superpozycji

Uproszczenie obliczeń wytrzymałościowych, rozbice układu złożonego na układy proste, suma da ukł początkowy; Nie stosować: σ w ukł wyjściowych p>σ_PROP, działnie 1 siły zmienia charakter 2-ściskanie i zginanie;

27. Naprężenia termiczne

၄l_t=၄tთlთၡ; ၄t- przyrost temp[ႰK]; l-dług. początkowa[m]; ၡ-współ. rozszerzalności liniowej

28. Naprężenia główne

ၳmax=(ၳ_x+ၳ_y)/2+r| ၳmin=(ၳ_x+ၳ_y)/2-r |r={[(ၳ_x+ၳ_y)/2]^2+ၴ^2}^(1/2)|

Wnioski W przekroju, w którym działają ekstremalne naprężenia normalne naprężenia styczne są zerowe(ၴ=0 ) Istnieją tylko 2 takie przekroje wzgl. siebie prostopadłe- przekroje główne. Napr. normalne działają w przekrojach głównych. gdy ၳ1>ၳ2 to zawsze ၳ2ႣၳၡႣၳ1|Kierunek działania max. naprężeń normalnych -kier. główne.

29. Maksymalne naprężenia styczne

Coulumb sformułował tzw. hipotezę największych naprężeń tnących (Tau max) : w czasie zwykłej próby uplastycznienie próbki (równoważone ze zniszczeniem) powstaje nie dlatego ze naprężenia rozciągające osiągnęły wartość σ pl, lecz dlatego ze największe naprężenia styczne Tau max osiągały wartość krytyczna, wynoszącą w przypadku zwykłego rozciapania Tau max = (L/alfa)* r_pl  

30. Wzór Steinera

Twierdzenie Steinera
Moment bezwładności I dowolnego ciała względem dowolnej osi jest równy sumie momentu bezwładności I_o względem osi równoległej przechodzącej przez środek masy ciała oraz iloczynu masy tego ciała i kwadratu odległości a obu osi: 

                 

Twierdzenia Steinera dla figury płaskiej
Moment bezwładności figury płaskiej względem osi równoległej do osi środkowej jest równy momentowi bezwładności tej figury względem jej osi środkowej, zwiększonemu o iloczyn pola figury i kwadratu odległości pomiędzy osiami.

                 

31. Odśrodkowy moment bezwładności

Dewiacyjny -J_YZ=∫_F yzdF- suma iloczynów pól dF i odl. środków ciężkości tych pól od osi współrz. y, z. Wartości +/-0.

32. Moment bezwładności

Momentem bezwładności układu mechanicznego względem nieruchomej osi a nazywamy wielkość fizyczną I_a równą sumie iloczynów mas wszystkich n punktów materialnych układu i kwadratów ich odległości od osi:

                 


gdzie m_i jest masą i-tego punktu, a r_i - jego odległością od osi.

Moment bezwładności ciała jest równy

                 


gdzie dm = r dV  jest masą małego elementu objętości bryły dV,
ρ - gęstością, a r - odległością elementu dV od osi a.

Moment bezwładności danej bryły względem dowolnej osi zależy od masy, kształtu i rozmiarów bryły oraz położenia bryły względem tej osi.

33. Zginanie

Czyste - występuje gdy układ sił zew w przekroju składa się tylko z Mg(ၞdo osi pręta);

Poprzeczne-też siła tnąca;

Proste-siła tnąca T i para sił powodująca zginanie pręta działają w1płasz.zawierającej osie centralne główne przekrojów poprzecz.- pł zginania i pł główna pokrywają się, oś pręta pozostaje nadal w płaszczyźnie;

Ukośne-nie spełniające warunku z prostego;

34. Wyboczenie

Wyboczeniem nazywamy zjawisko wyginania się pręta ściskanego siłami osiowymi. Wygięcie pręta spowodowane przekroczeniem przez siłę ściskającą wartości krytycznej. Siła w(krytycz):wartość s. po przekroczeniu której is utrata stateczności pręta(zmi. kszt. konstrukci)*zależy od dług. pręta, wielkości, kształtu przekroju, materiału, zamocowania końców .F_kr=π²EJ/L²[moduł sprężys. wzdłużnej; min. główny

35.Teoria Euler'a

Założenia :pręt jest początkwo prosty;materiał pręta jednorodny i izotropowy;pręt ma stały przekrój poprzeczny;naprężenia w pręcie są mniejsz od σprop.Siła rośnie b.wolno od małej wartości początkowej(postacie wyboczen)(P/E⋅J)^(1/2)=nΠ/L|P=n²π²EJ/L²| P_kr=π²EJ/L_s²|P=E(nπ/l)^2 podstawimy n i wychodzą Pkr.

36. Wpływ warunków podparcia

-Linie działania reakcji nie mogą przecinać się w jednym punkcie, nie pogą przecinać jedenj prostej i jednej płaszczyzny

- Wzdłuż jednej prostej może działać tylko jedna nieznana reakcja

- Ciało musi być podparte w co najmniej 3 (<6) miejscach nie leżących na jednej prostej

- Liczba reakcji więzów lub ich składowych <=6 jeżeli układ ma być statycznie wyznaczalny.

37. Naprężenia krytyczne

38. Hiperbola Euler'a
    

39. Teoria Rankinea

H. największe. napręż. normalnych-o wytężeniu materiału decyduje max .naprężenie normalne występujące w zagrożonym pkt. ciała.- jeżeli σ1>σ2>σ3 i σ1=σpl=σred -powoduje zniszczenie to σ2 i3 nie mają wpływu na stan wytężenia materiału;

40. Wytężenie materiału

Zmiany .w st .fizycznym materiału spowodowane jego stanem naprężenia i odkształcenia, które prowadzą do odkształceń trwałych, a w miarę wzrostu obciążenia do zniszczenia spójności materiału.-stopień narażenia mat. na zniszczenia na skutek oddział. mech.

41. Naprężenia zredukowane

Zastępcze napręż. rozciągające, powodujące takie samo niebezpieczeństwo zniszczenia materiału co i dany złożony stan naprężeń.

42. Siła tnąca

Siłą tnącą w danym przekroju poprzecznym belki nazywamy rzut na płaszczyznę tego przekroju wypadkowej wszystkich sił zewnętrznych działających na część belki odciętą tym przekrojem.
Obliczając siłę tnącą przez sumowanie sił zewnętrznych po lewej stronie przekroju, należy siły zewnętrzne zwrócone do góry uważać za dodatnie, a siły zwrócone w dół - za ujemne. Obliczając natomiast siłę tnącą przez sumowanie sił po prawej stronie przekroju, należy siły zewnętrzne zwrócone do góry uważać za ujemne, a siły zwrócone w dół za dodatnie.

43. Moment gnący

Momentem gnącym w danym przekroju belki nazywamy sumę momentów (względem środka ciężkości tego przekroju) wszystkich sił zewnętrznych działających na część belki odciętą tym przekrojem. Moment zginający uważamy za dodatni, jeśli wygina on belkę wypukłością ku dołowi. Momenty zginające wyginające belkę wypukłością do góry uważamy za ujemne.

44. Naprężenia przy czystym zginaniu

Założenia: belka początkowo prosta, promień krzywizny duży w porównaniu z wymiarami poprzecznymi belki; materiał belki jest jednoznaczny, sprężysty, obowiązuje prawo Hooke'a; materiał ma taki sam E dla rozciągania i ściskania, ၥ=(s'-s)/s, ၥ=-s/ၤ;naprężenia są równomierne, nie przekraczają granicy proporcjonalności; przekroje poprzeczne płaskie przed i po odkształceniu też płaskie i prostopadłe do zakrzywionej po odkształceniu osi belki; każde z włókien podłużnych może swobodnie wydłużać się lub skracać swą długość.

45. Oś obojętna

Oś centralna prostopadła do płaszczyzny

46. Moment elementarny siły

47. Naprężenia ekstremalne ściskające i rozciągające

48. Zginanie przekroju

49. Linia ugięcia belki.

W czasie pracy belka ulega odkształceniu. Początkowo prostoliniowa oś belki zmienia się na krzywoliniową. Krzywa ta nazywa się linią ugięcia osi belki. Przemieszczenie środka ciężkości przekroju w kierunku prostopadłym do osi belki nazywamy ugięciem belki, a największe ugięcie - strzałką ugięcia belki.

50. Warunki brzegowe.

51. Warunek równowagi

W ogólnym przypadku sił działających na ciało sztywne, równowaga możliwa jest, gdy suma geometr. tych sił=0 i gdy suma geom. ich mom. wzgl. dowolnego pktO=0

cos fi

T

---