UKŁADY RÓWNAŃ LINIOWYCH

1. Układy n równań o n niewiadomych

Rozważmy układ równań

(1)

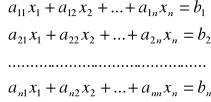
Wprowadzając zapis macierzy

A =

a11 a12 ... a1n a21 a22 ... a2n ................... ann an2 ... ann

= [aik]n×n n×n

B =

b1 b2 bn

n×1

X =

x1 x2 ... xn

n×1

możemy układ równań liniowych zastąpić równoważnym równaniem macierzowym

(2) A ^. X = B,

gdzie X jest macierzą niewiadomą, zaś A, B są danymi macierzami.

TWIERDZENIE 1 (Metoda macierzy odwrotnej)

Jeżeli det A ≠ 0, to istnieje dokładnie jedno rozwiązanie układu (1) zapisane w postaci macierzowej

X = A^-1B

Dowód :

Jeżeli równanie A^.X = B ma rozwiązanie, którym jest macierz X, to po pomnożeniu równania stronami lewostronnie przez macierz A^-1 (istniejącej z założenia) otrzymamy

A^{-1 .} (A ^. X) = A^{-1 .} B

(A^-1.A) ^. X = A^{-1 .} B

I ^. X = A^{-1 .} B

X = A^{-1 .} B

Uwaga 1

Macierz X = A^{-1 .} B jest rozwiązaniem równania A ^. X=B, ponieważ

L= A ^. X=A ^. (A^-1.B) = A ^. A^{-1 .}_­ B = I ^. B = B=P

Uwaga 2

Jeżeli macierz A jest nieosobliwa, to możemy zapisać:

(A|B) ~ (A^-1A|A^-1B) = (I|X)

i wówczas metoda powyższa nosi nazwę metody Gaussa-Jordana Jeżeli dokonamy przekształcenia (A|B) ~ (A^*|B^*) gdzie macierz A^* jest postaci

A^* =

1..[aik] 0 1 ... [aik] 0 0 .. 1

to przedstawiona metoda nosi nazwę metody eliminacji Gaussa

Układ równań liniowych nazywamy jednorodnym, gdy każdy wyraz wolny jest równy zero.

Wniosek 1

Jeżeli macierz A jest nieosobliwa, to układ jednorodny (3) posiada tylko rozwiązanie zerowe.

X = Ø =

0 0 ... 0

n×1

Wniosek 2

Jeżeli det A = 0, to wówczas:

1. układ niejednorodny jest sprzeczny - brak rozwiązań,

2. układ jednorodny jest nieoznaczony i posiada nieskończenie wiele rozwiązań niezerowych (poza rozwiązaniem zerowym).

TWIERDZENIE 2

Twierdzenie Cramera

Jeżeli W = det A ≠ 0, to układ (1) posiada dokładnie jedno rozwiązanie

X =

x1 x2 ... xn

n×1

określone wzorem

(i = 1, 2, ...), gdzie W_i jest to wyznacznik powstały z wyznacznika W przez zastąpienie i - tej kolumny, kolumną wyrazów wolnych.

Przykład 1

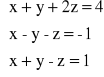
W = det A =

1 1 2 1-1-1 1 1-1

=

1 1 3 0 1 1 0

= 3

1-1 1 1

= 6

Metoda Cramera-metoda wyznaczników

W1 = Wx =

4 1 2 -1-1-1 1 1-1

=

4 1 3 0 0-2 1 1 0

= 2

4 1 1 1

= 6

W2 = Wy =

1 4 2 1-1 -1 1 1 -1

= 6

W3 = Wz =

1 1 4 1-1 -1 1 1 1

= 6

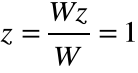
Przykład 2

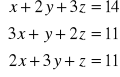
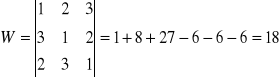
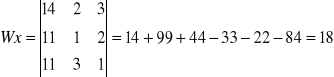
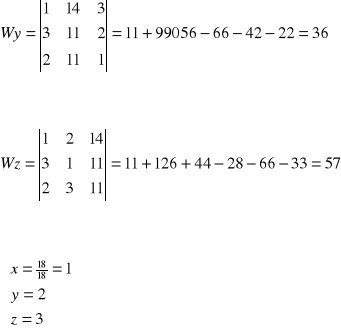
Przykład 3

Przykład 4

Rozwiązać układ równań:

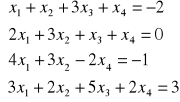
Obliczamy wyznacznik tego układu:

Ponieważ W = 0 to układ ten możemy rozwiązać z twierdzenia Cramera

Obliczamy wyznaczniki
,
,
,

= -96
= 2

= 96
= -2

= 48 i otrzymujemy
= -1

= -144
= 3

2. Układ m równań liniowych o n niewiadomych

(3)

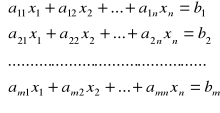
Wprowadzamy oznaczenia:

A =

a11 a12 ... a1n a21 a22 ... a2n ................... am1 am2 ...

jest macierzą współczynników przy niewiadomych m×n

B =

b1 b2 ... bm

jest macierzą wyrazów wolnych m×1

U= [A/B]

a11 a12 ... a1n a21 a22 ... a2n ................... am1 am2 ... amn

b1 b2 ... bm

jest macierzą uzupełnioną m×(n+1)

TWIERDZENIE Kroneckera - Capelliego

Jeżeli r(A) = r(U) = r, to układ (3) jest rozwiązywalny przy czym, gdy:

1. rząd r tych macierzy równa się liczbie niewiadomych n (r = n), to układ równań ma dokładnie jedno rozwiązanie

2. rząd r tych macierzy jest mniejszy od liczby niewiadomych n (r < n), to układ ma nieskończenie wiele rozwiązań, które zależą od n - r dowolnych parametrów.

Jeżeli r(A) ≠ r(U), to układ jest sprzeczny.

Przykład 1

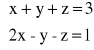
U = [A/B] =

1 1 1 2-1-1

3 1

W_­­² = -1 - 2 = -3 ≠ 0

r(A) = r(U) = r = 2

Wtedy n - r = 3 - 2 = 1 przyjmujemy za znany parametr np.z =

x + y = 3 - α 2x - y = 1 + α

z =

3x = 4

x =

y =
- α

Rozwiązaniem równania jest więc zbiór liczb: (
;
- α; α)

np. α = 1 (
;
; 1)

3. _{Układy równań jednorodnych}

_{Układ równań liniowych nazywa się jednorodny, gdy wszystkie wyrazy wolne są równe zeru.}

_{Macierz rozszerzona ma dodatkową kolumnę składającą się z samych zer, czego konsekwencją jest równość rzędów, bo kolumnowy zerowy wektor wyrazów wolnych jest liniowo zależny od wektorów kolumnowych macierzy A.}

_{Wobec tego:}

_{r(A) = r(U),}

_{stąd układ taki ma ZAWSZE rozwiązanie. Liczba rozwiązań tego układu wynika z twierdzenia Kroneckera-Capelliego.}

_{Przykład 1:}

_{Rozwiązać układ równań:}

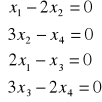
Na wstępie należy znaleźć rząd macierzy tego układu:

ponieważ wyznacznik macierzy A jest różny od zera,

to układ ma jedno rozwiązanie
, (układ Cramera jednorodny)

_{Przykład 2:}

_{Rozwiązać układ równań:}

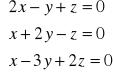
Macierz tego układu jest kwadratowa, obliczamy zatem wyznacznik tej macierzy:

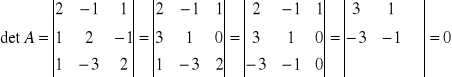
Ale:

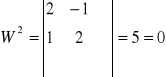
r(A)< 2

r(U)< 2

Z obliczeń wynika, że r(A)=r(U)=2 i na podstawie twierdzenia Kroneckera-Capelliego, układ ten ma nieskończenie wiele rozwiązań zależnych od n-r = 3-2 = 1 parametrów. Jeśli parametrem tym będzie zmienna z, to x i y znajdziemy z układu równań:

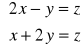
Układ ten ma rozwiązanie:

x =

y =

_z
R

Wektor rozwiązań ma więc postać: x = [
,
, z ], _z
R

_{Przykład 3:}

_{Rozwiązać układ równań:}

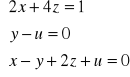
Obliczamy rzędy macierzy układu A i macierzy rozszerzonej U:

,

,

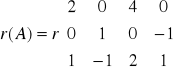
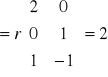
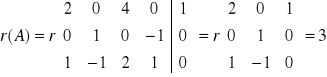
Widzimy, że r(A) = r(U), więc zgodnie z twierdzeniem Kroneckera-Capelliego, układ ten nie ma rozwiązań.

- 88 -

bo kolumny - druga z czwartą i pierwsza z trzecia są liniowo zależne.

bo detA=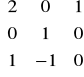
= -1 = 0

---