Z B I O R Y

Liczby naturalne, całkowite, wymierne i niewymierne:

Definicje i twierdzenia

Wśród pojęć matematycznych wyróżniamy:

-pojęcia pierwotne - nie definiujemy-punkt, liczba, zbiór

-definicje

-aksjomaty - pewniki, których nie wykazujemy, nie dowodzimy

-twierdzenia - składają się z założeń i tezy

założenie + teza = dowód

Algebra zbiorów. Iloczyn kartezjański zbiorów.

Jednym z pojęć pierwotnych matematyki jest pojęcie zbioru.

Dużymi literami alfabetu oznaczamy zbiory, małymi ich elementy, czyli przedmioty należące do zbioru.

Jeżeli element a należy do zbioru A, to zapiszemy a∈A, jeżeli a nie jest elementem zbioru A, to piszemy a∉A.

Zbiory są opisywane jednym z dwóch sposobów:

1. poprzez wymienienie wszystkich elementów zbioru np.: A={1,3,7}, lub

2. opisanie własności, którą posiadają wszystkie elementy tego zbioru i tylko one np.:B={x∈ℜ:2 x 5}.

Jeżeli wszystkimi elementami zbioru są a₁, a₂,..., a_n, to taki zbiór nazywamy zbiorem skończonym, i oznaczamy symbolem {a₁,a₂,..., a_n}.

Jeżeli do zbioru nie należy żaden element, to zbiór nazywamy zbiorem pustym, i oznaczamy symbolem ∅.

Natomiast zbiór, który nie jest skończony i nie jest pusty, nazywamy zbiorem nieskończonym.

Zatem zbiorem nieskończonym, jest na przykład zbiór liczb naturalnych czy zbiór liczb całkowitych.

Definicja:

Jeżeli każdy element zbioru A, jest elementem zbioru B, to mówimy, że zbiór A zawiera się w zbiorze B. (A⊂B).

Α⊂Β⇔∀ [(x∈Α)⇒(×∈Β)]

Np.:dla dwóch zbiorów A={1,3,5,7} i B={0,1,2,3,4,5,6,7,8} zbiór A zawiera się w zbiorze B (A⊂B lub inaczej zbiór A jest podzbiorem zbioru B).

Definicja:

Mówimy, że zbiór A jest równy zbiorowi B (A=B), jeżeli każdy element zbioru A jest elementem zbioru B i każdy element zbioru B jest elementem zbioru A.

Α=Β⇔∃ [(×∈Α)⇔(×∈Β)]

Możemy zauważyć, że:

Α=Β⇔[(Α⊂Β)∧(Β⊂Α)]

Definicja:

Sumą zbiorów A i B (A∪B) nazywamy zbiór tych elementów, które należą do zbioru A lub bo zbioru B.

Α∪Β={×:×∈Α∨×∈Β}

Przykład: niech będą dane zbiory:

A={3,5,8,12,23} i B={2,4,5,8,9,13,23} wówczas

A∪B={2,3,4,5,8,9,12,13,23}.

Definicja:

Iloczynem (częścią wspólną zbiorów A i B (A∩B) nazywamy zbiór tych elementów, które należą do zbioru A i do zbioru B.

Α∩Β={×:×∈Α∧×∈Β}

Przykład: Niech będą dane zbiory

A={15, 18, 40, 43} i B={10, 11, 18, 20, 40, 52}

to A∩B={18, 40}.

Definicja:

Różnicą zbiorów A i B (A\B) nazywamy zbiór tych elementów, które należą do zbioru A i nie należą do zbioru B.

A/B={×:×∈Α∧×∉Β}

Przykład: Dane są zbiory: A={-4, -2, 0, 5, 8, 10, 13}

B={-1, 0, 7, 12, 13, 18}

To A\B={-4, -2, 5, 8, 10}

Definicja:

Zbiory A i B nazywamy zbiorami rozłącznymi, gdy ich iloczyn jest zbiorem pustym (to znaczy nie mają ani jednego wspólnego elementu).

Α∩Β=∅

Wszystkie rozważane zbiory należą do pewnego ustalonego zbioru X. Zbiór ten nazywamy przestrzenią.

Definicja:

Dopełnieniem zbioru a jest zbiór, który zawiera wszystkie elementy nie należące do zbioru a.

Ω a∈Α′⇔a∉A

Zbiór uniwersalny - Ω

Przykład:

Jeżeli traktujemy zbiór liczb rzeczywistych ℜ jako przestrzeń, to dopełnieniem zbioru liczb dodatnich jest zbiór liczb rzeczywistych niedodatnich.

Niektóre prawa algebry zbiorów

- przemienności

a) Α∪Β=Β∪Α

b) Α∩Β=Β∩Α

- łączności

c) Α∪(Β∪C)=(Α∪Β)∪C

d) Α∩(Β∩C)=(Α∩Β)∩C

- rozdzielności

e) Α∩(Β∪C)=(Α∩Β)∪(Α∩C)

f) Α∪(Β∩C)=(Α∪Β)∩(Α∪C)

- tautologii

g) Α∪Α=Α

h) Α∩Α=Α

i) Α∪∅=Α

j) Α∩∅=∅

- de Morgana:

k) Α′∪Β′=(Α∩Β)′

l) Α′∩Β′=(Α∪Β)′

Iloczyn kartezjański zbiorów

Rozważmy teraz zbiór dwuelementowy {a, b} gdzie a b.

Z określenia równości zbiorów wynika, że {a, b}={b, a}

Jeśli jednak jeden z elementów tego zbioru np. a uznamy za pierwszy element, a b za drugi, to otrzymamy parę uporządkowaną (a, b)

a - pierwszy element pary nazywamy poprzednikiem

b - drugi element - następnikiem.

Definicja:

Iloczynem kartezjańskim zbiorów A i B Α×Β nazywamy zbiór wszystkich par uporządkowanych (a, b) takich, że a∈Α i b∈B

Α×Β={(a, b):a∈Α∧b∈Β}

Przykład:

Niech dane będą zbiory A={1, 3, 7} i B={2, 5} wówczas:

Α×Β={(1, 2); (1, 5); (3, 2); (3, 5); (7, 2); (7, 5)}

oraz

Β×Α={(2,1); (2, 3); (2, 7); (5, 1); (5, 3); (5, 7)}

łatwo zauważyć, że

Α×Β≠Β×Α

Liczby naturalne, całkowite i niewymierne

Znanymi nam zbiorami liczbowymi, które są jednocześnie podzbiorami zbioru liczb rzeczywistych ℜ są :

Zbiór liczb naturalnych - oznaczany przez N,

Zbiór liczb całkowitych - oznaczany przez C,

Zbiór liczb wymiernych - oznaczany przez W,

Zbiór liczb niewymiernych - oznaczany przez NW.

Liczby naturalne to :0,1,2,3,4,..., czyli zbiór N={0,1,2,3,...}.

W zbiorze tym istnieje liczba najmniejsza 0. Nie istnieje natomiast największa, ponieważ dla n∈N, także (n+1)∈N. Zbiór liczb naturalnych jest nieskończony.

Liczby całkowite to liczby naturalne i liczby do nich przeciwne, czyli C={...,-3,-2,-1,0,1,2,3,...}. W tym zbiorze nie istnieje ani liczba najmniejsza ani największa, jest on również zbiorem nieskończonym.

Do zbioru liczb wymiernych należy każda liczba, którą można przedstawić w postaci ułamka
gdzie p∈C, q∈C/{0}. Np.
;
;
-
itd. Jeżeli p,q∈N i q≠0 oraz p<q, to ułamek
nazywamy ułamkiem właściwym. Jeżeli natomiast p≥q to
jest ułamkiem niewłaściwym.

Ułamki o mianownikach 10, 100, 1000,..., to ułamki dziesiętne. Są zapisywane w dziesiątkowym systemie pozycyjnym z przecinkiem oddzielającym część całkowitą od ułamkowej Np.
=0,7;
=0,15;
=0,147 itd.

Aby zamienić ułamek zwykły np. na ułamek dziesiętny, można wykonać dzielenie 7÷20=0,35 - rozwinięcie dziesiętne skończone

Zamiana ułamka
na ułamek dziesiętny.

Po wykonaniu dzielenie otrzymamy : 8÷9=0,888...=0,(8) - rozwinięcie dziesiętne nieskończone okresowe.

Twierdzenie :

Każda liczba wymierna ma dokładnie jedno rozwinięcie dziesiętne skończone, albo nieskończone okresowo i odwrotnie, każde rozwinięcie dziesiętne nieskończone i każde rozwinięcie dziesiętne skończone są rozwinięciami dziesiętnymi liczb wymiernych.

Liczbami niewymiernymi nazywamy takie liczby, których nie można przedstawić w postaci ułamka
gdzie p∈C i q∈C/{0}.

Np.

, π

Rozwinięcie dziesiętne liczby niewymiernej jest nieskończone i nieokresowe.

Między zbiorami liczbowymi zachodzą następujące zależności N⊂C⊂W⊂R, W∪NW=R, W∩NW=∅ (ostatnia równość oznacza, że zbiory liczb wymiernych i zbiory liczb niewymiernych są rozłączne).

Przedstawione zależności można zinterpretować graficznie :

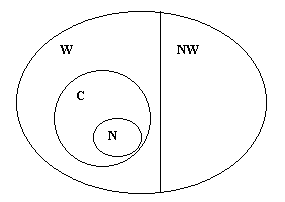
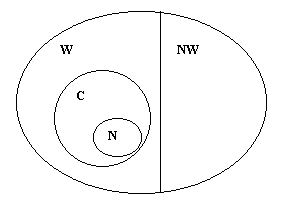
Zbiory ograniczone, nieograniczone, kres górny i dolny zbiorów

Niech Z będzie dowolnym niepustym podzbiorem zbioru liczb rzeczywistych.

Definicja:

Zbiór Z nazywamy ograniczonym z góry, jeżeli istnieje liczba A, nie mniejsza od każdego elementu tego zbioru.

Tzn. ×≤Α

O liczbie A mówimy, że ogranicza zbiór Z z góry.

Np.: zbiór liczb całkowitych ujemnych jest ograniczony z góry przez liczby -1,0, 7, 15 itd.

Definicja:

Zbiór Z nazywamy ograniczonym z dołu, jeżeli istnieje liczba B, nie większa od każdego elementu tego zbioru.

Tzn. ×≥Β

O liczbie B mówimy, że ogranicza zbiór Z z dołu.

Np.: zbiór liczb naturalnych ujemnych jest ograniczony z dołu przez liczby 0, -3, -101 itd.

Definicja:

Zbiór Z nazywamy ograniczonym gdy jest ograniczony z dołu i z góry.

Np. Zbiór wszystkich ułamków właściwych dodatnich jest ograniczony z góry przez 1 i wszystkie liczby większe od 1, a z dołu przez 0 i wszystkie liczby mniejsze od 0.

Definicja:

Kresem górnym zbioru ograniczonego z góry nazywamy najmniejszą liczbę ograniczającą ten zbiór z góry.

Kres górny zbioru A oznaczamy symbolem supA.

Np.:Kresem górnym zbioru liczb całkowitych ujemnych, który jest ograniczony z góry przez

-1 i wszystkie liczby większe od -1 jest -1 supC_-=-1.

Definicja:

Kresem dolnym zbioru ograniczonego z dołu nazywamy największą liczbę ograniczającą ten zbiór z dołu.

Kres dolny zbioru A oznaczamy symbolem infA.

Np.:Kresem dolnym zbioru ułamków właściwych dodatnich U jest liczba 0 infU=0 (supU=1).

Działania w zbiorze liczb rzeczywistych.

W zbiorze liczb rzeczywistych określone są cztery działania arytmetyczne:

- dodawanie x + y = t (x,y-składniki; t-suma)

- odejmowanie x - y = z (x-odjemna, y-odjemnik; z-różnica)

- mnożenie x ⋅ y = k (x,y-czynniki; k-iloczyn)

- dzielenie x ÷ y = l (x-dzielna, y-dzielnik; l-iloraz, y≠0)

Odejmowanie jest działaniem odwrotnym do dodawania, dzielenie jest działaniem odwrotnym do mnożenia.

Elementem neutralnym (obojętnym, modułem) dodawania jest liczba 0 ponieważ dla każdego x:x+0=x

Elementem neutralnym mnożenia jest liczba 1 ponieważ dla każdego x:x⋅1=x

Jeżeli obliczamy wartość wyrażeń nie zawierających nawiasów działania wykonujemy w następującym porządku: mnożenie lub dzielenie, a następnie dodawania lub odejmowanie.

Definicja:

Niech n będzie liczba naturalną dodatnią, wówczas dla dowolnej liczby rzeczywistej a:

=
...

n czynników, gdzie :

nazywamy potęgą o podstawie a i wykładniku n

Ponadto
;

dla a≠0

Własności działań na potęgach

Dla każdej pary liczb rzeczywistych a i b oraz liczb naturalnych dodatnich m i n zachodzą wzory :

dla
i m>n

dla

Wzory skróconego mnożenia:

kwadrat sumy (a+b)²=a²+2ab+b²

kwadrat różnicy (a-b)²=a²-2ab+b²

sześcian sumy (a+b)³=a³+3a²b+3ab²+b³

sześcian różnicy (a-b)³=a³-3a²b+3ab²-b³

różnica kwadratów a²-b²=(a-b)(a+b)

różnica sześcianów a³-b³=(a-b)(a²+ab+b²)

suma sześcianów a³+b³=(a+b)(a²-ab+b²)

Pierwiastkiem arytmetycznym stopnia n∈N₊/{1} z liczby nieujemnej a nazywamy taką liczbę nieujemną b, że bⁿ=a. Liczbę tę oznaczamy :

Pierwiastek stopnia drugiego z liczby a≥0 oznaczamy symbolem
.

Własności działań na pierwiastkach

Dla każdej pary liczb rzeczywistych a i b oraz liczb naturalnych m i n, gdzie m,n∈N₊/{1} zachodzą wzory:

dla

Przykład :

Usuń niewymierność z mianownika
;

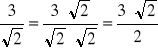
Definicja :

Wartość bezwzględną liczby x oznaczamy symbolem |×| i określamy w następujący sposób :

|×|={x dla x≥0, -x dla x<0}

to znaczy, że wartość bezwzględna liczby nieujemnej jest tą samą liczbą, a wartość bezwzględna liczby ujemnej jest liczbą do niej przeciwną.

Np.|7|=7; |-3|=3; |0|=0

Z określenia pierwiastka arytmetycznego i wartości bezwzględnej wynika, że :

dla każdego

Natomiast pierwiastek stopnia nieparzystego z liczby ujemnej a został określony następująco :

np.:

Dla zdefiniowanej wartości bezwzględnej zachodzą następujące zależności :

Dla każdego x,y∈R i b>0 :

1.|×|≥0

2.|×|=|−×| w szczególności |×−y|=|y−×|

3.|×⋅y|=|×|⋅|y|

4.|×+y|≤|×|+|y|

5.|×−y|≥|×|−|y|

6.|×|<b⇔−b<×<b⇔×∈(-b,b)

7.|×|>b⇔(×<−b∨×>b)⇔[×∈(−∞;b)∪(b;∞)]

Przykład:

Dla jakich x prawdziwa jest równość: |3x-7|=−(3×−7) ?

Zgodnie z definicją wartości bezwzględnej mamy :

|3x-7|=−(3×−7)⇔3×−7<0⇔3×<7⇔×<
⇔×∈(−∞;
)

Dla jakich x prawdziwa jest nierówność : |2x-3|<4?

z własności 6 mamy:

|2x-3|<4⇔−4<2×−3<4⇔−4+3<2×<4+3⇔−1<2×<7⇔

−
<x<
⇔×∈

Dla jakich x prawdziwa jest nierówność : |4−3×|>7?

z własności 7 mamy:

|4−3×|>7⇔(4−3×<−7∨4−3×>7)⇔(−3×<−7−4∨−3×>7−4)⇔

(−3×<−11∨−3×>3)⇔(×>
∨×<−1)⇔[×∈(−∞;−1)∨(
;∞)]

---