Sprawozdanie z ćwiczenia nr 41.

Michał Tyszko

Marcin Wróblewski

Zespół 8

Wyznaczanie energii promieniowania
za pomocą spektrometru scyntylacyjnego.

Celem ćwiczenia jest zapoznanie się z zasadą działania spektrometru scyntylacyjnego i typowym kształtem widma impulsów otrzymywanych w wyniku rejestracji promieniowania γ. W trakcie ćwiczenia wykorzystywaliśmy źródła ⁶⁰Co, ¹³⁷Cs, w celu dokonania kalibracji spektrometru, ²²Na w celu porównania energii pików wyznaczonych przez nas z danymi tabelarycznymi oraz wyznaczenie energii kwantów γ, krawędzi Comptona.

Należy przy tym zauważyć iż mierzone przez nas piki przy źródłach ⁶⁰Co, ¹³⁷Cs są wynikami zjawiska fotoelektrycznego zachodzącego pod wpływem kwantów energii promieniowania γ. W rezultacie tego zjawiska energia kwantu promieniowania γ zostaje spożytkowana na wybicie pojedynczego elektronu z atomu i nadaniu mu określonego pędu, oraz emisji promieniowania rentgenowskiego które jest jednak pochłaniane przez ośrodek. W wyniku zachodzenia wyżej opisanych zjawisk, energia tracona w spektrometrze jest równa energii kwantu γ.

Drugim zjawiskiem którego parametry wyznaczaliśmy było zjawisko krawędzi Comptona. Polega ono na rozproszeniu kwantu γ na swobodnym elektronie, atomu. W wyniku tego zjawiska elektron nabywa energię kinetyczną , foton (nośnik energii kwantu γ) zmienia kierunek.

Kolejnym zjawiskiem obserwowanym w przypadku sodu jest tworzenie się par elektron - pozytron, możliwe jest przy odpowiednio dużych energiach kwantów γ. Polega ono na całkowitej zamianie energii kwantu γ na energie spoczynkowe i kinetyczne dwu cząstek, zjawisko to jednak zachodzi tylko w obecności cząsteczki trzeciej która przejmuje część energii i pędu, zgodnie z zasadą zachowania energii. Elektron i pozytron ulegają wielokrotnemu rozproszeniu w ośrodku, do momentu w który następuje anihilacja, i emisja kwantów γ o energii 0,511 Mev każdy, które zostaną zaobserwowane w efekcie fotoelektrycznym.

Wykonanie ćwiczenia.

1. Najpierw wykonaliśmy pomiary kalibracyjne, umieszczając w domku pomiarowym kolejno
i
. Wyniki pomiarów zamieszczamy w tabeli poniżej:

Źródło	Pik	Kanał	Szerokość połówkowa	N	Środek krawędzi Comptona	Energie kwantów [MeV]
^137Cs	I	1893	225	2170	1349	0,66
^60Co	I	3160	308	2860		1,173
		II	3568	286	2100		1,332

Przeprowadziliśmy kalibrację energetyczną polegającą na wyznaczeniu współczynników równania kalibracyjnego w postaci:

gdzie: E - energia kwantu stracona w scyntylatorze, kan - numer kanału.

Współczynniki równania a i b oraz ich błędy wyznaczyliśmy przy pomocy programu komputerowego Microsoft Excel i funkcji REGLIMP, wykorzystując uzyskane w pomiarach numery kanałów i odpowiadające im energii kwantów emitowanych przez
i
.

Otrzymalismy nastepujace wyniki:

	-0,10042559 0,00879596

Następnie wykonaliśmy wykres energii w zależności od numeru kanału.

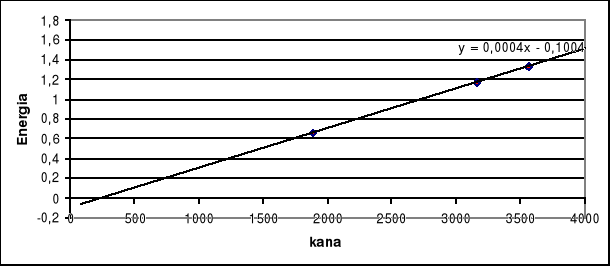
2. Dokonaliśmy pomiaru ze źródłem
, notując dane dla piku pochodzącego z anihilacji pozytonu (I) i promieniowania
emitowanego z jądra
(II).

Źródło	Pik	Kanał	Szerokość połówkowa	N	Energie kwantów [MeV]
^22Na	I	1491	182	13430	0,511
		II	3408	314	1457	1,28

Korzystając z prostej kalibracyjnej określiliśmy energię promieniowania
pochodzącego z
i sprawdziliśmy zgodność z wartościami odczytanymi z instrukcji.

Pik	Kanał	[MeV]	Wartości tablicowe [MeV]
I	1491		0,511
II	3408		1,28

3. Biorąc pod uwagę błędy wyznaczania współczynników równania kalibracyjnego, ustaliliśmy przedziały wartości między którymi mieści się szukana energia.

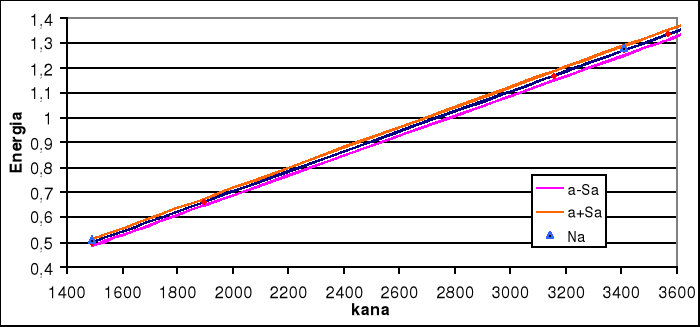
	Przedziały wartości		E wyznaczona [MeV]	E tablicowa [MeV]
I	0,486	0,512	0,500	0,511
II	1,251	1,289	1,270	1,28

4. Sprawdziliśmy również czy dokładność wyznaczania energii promieniowania zależy od wartości tej energii. Błąd wyznaczania energii liczymy posługując się różniczką zupełną:

Kanał (kan)	Szerokość połówkowa ( )
1893	225	0,159
3160	308	0,121
3568	286	0,101
1491	182	0,173
3408	314	0,114

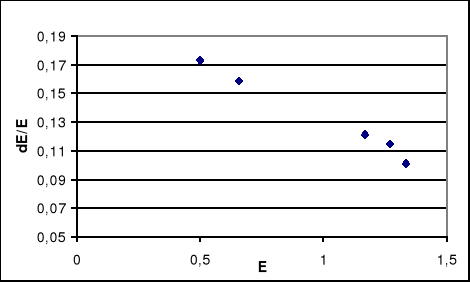
Poniżej wykonaliśmy wykres błędu względnego energii
w funkcji energii
i doszliśmy do wniosku, że błąd względny maleje ze wzrostem energii kwantu.

5. Posługując się równaniem :

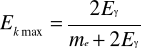
Po przekształceniu do równania równoważnego:

podstawiając wyliczoną z równania kalibracyjnego energię kinetyczną elektronu krawędzi Comptona - dla widma ¹³⁷Cs - Ek _max = 0,442 MeV, otrzymaliśmy energie kwantu γ
.

3

---