Imię i nazwisko	Ćwiczenie nr 3 Badanie polaryzacji światła
Kierunek i rok Fizyka Mag. Uzup. I	Ocena z kolokwium	Ocena ze sprawozdania	Ocena końcowa
Prowadzący ćwiczenia

Część teoretyczna

Metody polaryzacji światła

Polaryzacja światła przez podwójne załamanie

Na skutek zjawiska podwójnego załamania światło ulega rozproszeniu na dwie wiązki, zwyczajna i nadzwyczajną, mają one pewne cechy, których nie ma wiązka pierwotna. Udowodnimy to rzucając wiązkę światła prostopadle na płasko-równoległą płytkę za szpatu islandzkiego. Wiązka zostaje rozdzielona na dwie wiązki zwyczajną i nadzwyczajną, przy czym wiązka zwyczajna przechodzi bez zmian kierunku, a nadzwyczajna ulega odchyleniu. Obracając kryształ dokoła promienia zwyczajnego, wiązka nadzwyczajna zatoczy okrąg, lecz jej natężenie pozostanie bez zmian.

Odwrotnie sytuacja będzie się miała, jeśli promień zwyczajny rzucimy na drugi kryształ szpatu, również w formie płytki. Wówczas promieni ten ulegnie znów rozproszeniu na wiązkę zwyczajną i nadzwyczajną. Gdy teraz będziemy obracać drugi kryształ wiązka nadzwyczajna znów zatacza okrąg, lecz tym razem w miarę obrotu zauważymy periodyczną zmianę natężenia obu wiązek. W pewnym położeniu drugiego kryształu obie wiązki są jednakowo jasne; przy dalszym obrocie zauważymy zaciemnienie wiązki nadzwyczajnej, a rozjaśnienie zwyczajnej. Wreszcie wiązka nadzwyczajna znika, a pozostaje tylko wiązka zwyczajna. Następnie pojawia się znów nadzwyczajna, a zwyczajna staje się słabsza. Dalej dochodzi do płożenia, gdy wiązka nadzwyczajna zostaje, a wiązka zwyczajna wygasa itd.

Te zmiany natężenia stanowią cechę wyróżniającą wiązkę zwyczajną w stosunku do światła zwykłego. Promień zwyczajny i nadzwyczajny są spolaryzowane liniowo i drgania wektora świetlnego, zachodzą w płaszczyznach wzajemnie do siebie prostopadłych.

Polaryzacja światła przez odbicie

Jeżeli kąt padania jest tak dobrany, by kąt miedzy promieniem odbitym i załamany wynosił 90
, wtedy promień orbity jest całkowicie liniowo spolaryzowany w płaszczyźnie padania, a promień załamany spolaryzowany jest częściowo w płaszczyźnie prostopadłej do płaszczyzny padania.

Zjawisko powyższego można również wykorzystać do polaryzowania światła. Chcąc uzyskać całkowitą polaryzację światła załamanego musimy przepuścić je przez wiele równoległych płytek załamujących. Zjawisko to jako pierwszy opisał Malus w roku 1808.

Malus zauważył, że jeśli wiązkę odbitą od szyby szklanej rzucimy pod tym samym kątem na drugą szybę, to natężenie wiązki powtórnie odbitej zależy w prawidłowy sposób od kata, który tworzą z sobą płaszczyzny padania światła na pierwszą i drugą płytkę. Największe natężenie wiązki powtórnie odbitej od drugiej szyby uzyskujemy wówczas, gdy te płaszczyzny padania są do siebie równoległe. Gdy zaczniemy je skręcać względem siebie, natężenie wiązki odbitej maleje i staje się najmniejsze, gdy płaszczyzny są do siebie prostopadłe. Przy dalszym obrocie natężenie znów wzrasta aż do wartości kąta 180
, następnie znów maleje itd. A zatem bardzo wyraźnie występują w tym przypadku dwie prostopadłe do siebie płaszczyzny symetrii.

Prawo Malusa

Gdy kąt miedzy charakterystycznymi kierunkami polaryzacji - płaszczyzną polaryzacji światła a płaszczyzną drgań przepuszczanych przez analizator - wynosi
, wtedy natężenie I wiązki światła po przejściu analizatora będzie równe

gdzie I
, maksymalne natężenie światła. Maksymalne natężenie otrzymamy, gdy kąt
między polaryzatorem a analizatorem jest równy 0 lub 180
.

Efekt elektrooptyczny Pockelsa

Efektem elektrooptycznym nazywamy wymuszoną (indukowaną) polem elektrycznym zmianę orientacji i wymiarów współczynnika załamania.

Efektem elektrooptyczny Pockelsa nazywamy zależność zmiany współczynnika załamania od pola elektrycznego.

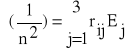
i = 1,2,.....6

j = 1,2,3

Efekt ten nie występuje w kryształach, które mają środek symetrii

Laser półprzewodnikowy działa podobnie jak diody świecące LED (skrót od angielskiego emitting diode). LED zamieniają energię elektryczną na światło widzialne lub promieniowanie podczerwone. Źródłem światła jest złącze półprzewodnikowe n-p. Światło powstaje w wyniku tego, że elektrony w paśmie przewodnictwa są pobudzane do rekombinacji z dziurami w paśmie walencyjnym. Gdy zachodzi to zjawisko, elektrony oddają energię odpowiadającą przerwie wzbronionej i następuje świecenie. Do tych celów przydatne są takie materiały jak arsenek galu lub azotek galu, a obecnie częściej cienkie warstwy półprzewodników. Diody LED wysyłają światło niespójne i nie do końca monochromatyczne. Aby powstał laser należy tak uformować układ aby powstał rezonator optyczny. Gdy do złącza będą wstrzykiwane duże ładunki to może w nim powstać proces laserowy i w wyniku wymuszonych przejść z pasma przewodnictwa do walencyjnego generuje się spójna wiązka światła. Zwierciadłami lasera mogą być krawędzie kryształu. Lasery półprzewodnikowe mogą być miniaturowe i nie przekraczają długości 1 mm. Nie jest to na ogól jednak wiązka skupiona i o stosunkowo małej mocy.

Fotoogniwo nie wymaga źródła zasilania, ponieważ samo jest źródłem siły elektromotorycznej rzędu woltów. Wykonuje się je najczęściej w postaci przezroczystej warstwy półprzewodnika, np. selenu, naniesionego na płytkę metalową. Ogniwa o tylnej warstwie światłoczułej są najbardziej czułe na światło czerwone, natomiast ogniwa o przedniej warstwie światłoczułej - na światło niebieskie. Ogniwo fotoelektryczne ma oporność wewnętrzną 10
do 10
Ω. Dlatego charakterystyka świetlna ogniwa jest liniowa jedynie w przypadku zastosowania opornika zewnętrznego R o małym oporze (około 100 Ω). Fotoogniwo selenowe ma czułość widmową zbliżoną do czułości oka ludzkiego. Duża pojemność własna uniemożliwia pracę fotoogniwa przy większych częstotliwościach. Natomiast stosunkowo duża czułość rzędu 500μA/lm umożliwia bezpośrednie włączanie ich w obwód mikroamperomierza lub galwanometru, jak np. w światłomierzach fotograficznych.

Charakterystyka prądowo-napięciowa fotoogniwa

Fotodioda jest diodą w której na wartość prądu można wpływać przez zmianę natężenia promieniowania elektromagnetycznego padającego na określoną jej powierzchnię np. fotokatodę lub złącze p-n. Działanie fotodiody polega na wykorzystaniu zjawiska fotoelektrycznego zewnętrznego ( fotodiody: próżniowe i gazowe ) lub wewnętrznego (fotodiody półprzewodnikowe). Fotodiodę polaryzuje się w kierunku zaporowym, a napromienienie złączy powoduje wzrost liczby nośników w paśmie przewodnictwa. Niekorzystny jest wpływ temperatury, gdyż wzrost temp. powoduje wzrost prądu ciemnego.

Przy braku oświetlenia przez fotodiodę płynie niewielki ciemny prąd wsteczny I
, tworzą go głównie nośniki mniejszościowe. Przy oświetleniu fotodiody, w pobliżu jej powierzchni są generowane pary nośników dziura - elektron. Obszar ładunku przestrzennego i związana z nim bariera potencjału uniemożliwiają przepływ nośników większościowych, natomiast nośniki mniejszościowe (tj. dziury w obszarze N i elektrony w obszarze P) dyfundują do obszaru ładunku przestrzennego, są przyspieszane i pokonują złącze.

Charakterystyka prądowo-napięciowa fotodiody

Część praktyczna

Dokonałem pomiaru zależności natężenia prądu fotoogniwa od kąta skręcenia analizatora, pomiary wykonałem w przedziale od 0
do 360
> przy pomiarach uwzględniłem prąd ciemny I
detektora, który wynosi
. Wyniki pomiaru przedstawiłem w tabeli I.

Tabela I

Lp.	α [ ]	I [μA]	I/I [μA]	cos α	Lp.	α [ ]	I [μA]	I/I [μA]	cos α
1	0	620	885,7143	1	38	185	580	828,5714	0,992404
2	5	600	857,1429	0,992404	39	190	540	771,4286	0,969846
3	10	540	771,4286	0,969846	40	195	480	685,7143	0,933013
4	15	500	714,2857	0,933013	41	200	440	628,5714	0,883022
5	20	440	628,5714	0,883022	42	205	380	542,8571	0,821394
6	25	400	571,4286	0,821394	43	210	320	457,1429	0,75
7	30	340	485,7143	0,75	44	215	280	400	0,67101
8	35	280	400	0,67101	45	220	220	314,2857	0,586824
9	40	220	314,2857	0,586824	46	225	180	257,1429	0,5
10	45	180	257,1429	0,5	47	230	140	200	0,413176
11	50	140	200	0,413176	48	235	80	114,2857	0,32899
12	55	100	142,8571	0,32899	49	240	40	57,14286	0,25
13	60	60	85,71429	0,25	50	245	28	40	0,178606
14	65	20	28,57143	0,178606	51	250	8	11,42857	0,116978
15	70	12	17,14286	0,116978	52	255	2	2,857143	0,066987
16	75	2,4	3,428571	0,066987	53	260	4,2	6	0,030154
17	80	3,4	4,857143	0,030154	54	265	18	25,71429	0,007596
18	85	14	20	0,007596	55	270	38	54,28571	3,38E-32
19	90	32	45,71429	3,75E-33	56	275	70	100	0,007596
20	95	62	88,57143	0,007596	57	280	100	142,8571	0,030154
21	100	96	137,1429	0,030154	58	285	160	228,5714	0,066987
22	105	140	200	0,066987	59	290	200	285,7143	0,116978
23	110	200	285,7143	0,116978	60	295	240	342,8571	0,178606
24	115	240	342,8571	0,178606	61	300	300	428,5714	0,25
25	120	280	400	0,25	62	305	360	514,2857	0,32899
26	125	340	485,7143	0,32899	63	310	400	571,4286	0,413176
27	130	400	571,4286	0,413176	64	315	460	657,1429	0,5
28	135	440	628,5714	0,5	65	320	520	742,8571	0,586824
29	140	500	714,2857	0,586824	66	325	560	800	0,67101
30	145	540	771,4286	0,67101	67	330	600	857,1429	0,75
31	150	580	828,5714	0,75	68	335	620	885,7143	0,821394
32	155	600	857,1429	0,821394	69	340	640	914,2857	0,883022
33	160	620	885,7143	0,883022	70	345	640	914,2857	0,933013
34	165	640	914,2857	0,933013	71	350	640	914,2857	0,969846
35	170	640	914,2857	0,969846	72	355	620	885,7143	0,992404
36	175	620	885,7143	0,992404	73	360	620	885,7143	1
37	180	600	857,1429	1

Otrzymane wyniki posłużyły mi do przedstawienia graficznych zależności:

I = f(α)

I/I
= f(α)

I/I
= f(cos
α)

W drugiej cześć doświadczenia do układu pomiarowego dołączyłem komórkę Pockelsa (patrz efekt elektrooptyczny Pockelsa), ustawiłem polaryzator pod kątem 45
do kierunku pola elektrycznego przykładanego do kryształu umieszczonego wewnątrz komórki Pockelsa. Wykonywałem pomiary zależności natężenia prądu fotoogniwa od napięcia przykładanego do komórki Pockelsa w zakresie napięć 0-1300 V co 20V oraz od 0+1300 V co 20V. Przy pomiarach uwzględniłem prąd ciemny I
detektora, który wynosi
. Wyniki pomiaru przedstawiłem w tabeli II dla +U i w tabeli III dla -U.

Tabela II

Lp.	U [V]	I [μA]	I/I [μA]	Lp.	U [V]	I [μA]	I/I [μA]
1	0	1,6	0,9	34	660	1,85	1,15
2	20	1,6	0,9	35	680	1,8	1,1
3	40	1,6	0,9	36	700	1,8	1,1
4	60	1,65	0,95	37	720	1,75	1,05
5	80	1,7	1	38	740	1,7	1
6	100	1,7	1	39	760	1,7	1
7	120	1,7	1	40	780	1,7	1
8	140	1,75	1,05	41	800	1,65	0,95
9	160	1,8	1,1	42	820	1,6	0,9
10	180	1,8	1,1	43	840	1,6	0,9
11	200	1,8	1,1	44	860	1,5	0,8
12	220	1,85	1,15	45	880	1,5	0,8
13	240	1,9	1,2	46	900	1,45	0,75
14	260	1,9	1,2	47	920	1,4	0,7
15	280	1,9	1,2	48	940	1,4	0,7
16	300	1,9	1,2	49	960	1,35	0,65
17	320	1,95	1,25	50	980	1,3	0,6
18	340	1,95	1,25	51	1000	1,3	0,6
19	360	2	1,3	52	1020	1,25	0,55
20	380	2	1,3	53	1040	1,2	0,5
21	400	2	1,3	54	1060	1,2	0,5
22	420	2	1,3	55	1080	1,2	0,5
23	440	2	1,3	56	1100	1,15	0,45
24	460	2	1,3	57	1120	1,15	0,45
25	480	2	1,3	58	1140	1,1	0,4
26	500	2	1,3	59	1160	1,1	0,4
27	520	2	1,3	60	1180	1,1	0,4
28	540	2	1,3	61	1200	1,1	0,4
29	560	1,95	1,25	62	1220	1,1	0,4
30	580	1,9	1,2	63	1240	1,1	0,4
31	600	1,9	1,2	64	1260	1,1	0,4
32	620	1,9	1,2	65	1280	1,1	0,4
33	640	1,85	1,15	66	1300	1,15	0,45

Tabela III

Lp.	U [V]	I [μA]	I/I [μA]	Lp.	U [V]	I [μA]	I/I [μA]
1	0	1,6	0,9	34	660	1,7	1
2	20	1,6	0,9	35	680	1,7	1
3	40	1,6	0,9	36	700	1,7	1
4	60	1,55	0,85	37	720	1,7	1
5	80	1,55	0,85	38	740	1,7	1
6	100	1,55	0,85	39	760	1,65	0,95
7	120	1,5	0,8	40	780	1,65	0,95
8	140	1,5	0,8	41	800	1,65	0,95
9	160	1,5	0,8	42	820	1,65	0,95
10	180	1,5	0,8	43	840	1,6	0,9
11	200	1,5	0,8	44	860	1,6	0,9
12	220	1,5	0,8	45	880	1,6	0,9
13	240	1,5	0,8	46	900	1,6	0,9
14	260	1,5	0,8	47	920	1,55	0,85
15	280	1,5	0,8	48	940	1,5	0,8
16	300	1,5	0,8	49	960	1,5	0,8
17	320	1,5	0,8	50	980	1,5	0,8
18	340	1,5	0,8	51	1000	1,45	0,75
19	360	1,5	0,8	52	1020	1,4	0,7
20	380	1,5	0,8	53	1040	1,4	0,7
21	400	1,55	0,85	54	1060	1,4	0,7
22	420	1,55	0,85	55	1080	1,35	0,65
23	440	1,6	0,9	56	1100	1,3	0,6
24	460	1,6	0,9	57	1120	1,3	0,6
25	480	1,6	0,9	58	1140	1,3	0,6
26	500	1,6	0,9	59	1160	1,25	0,55
27	520	1,6	0,9	60	1180	1,25	0,55
28	540	1,6	0,9	61	1200	1,2	0,5
29	560	1,65	0,95	62	1220	1,2	0,5
30	580	1,65	0,95	63	1240	1,2	0,5
31	600	1,65	0,95	64	1260	1,15	0,45
32	620	1,65	0,95	65	1280	1,15	0,45
33	640	1,7	1	66	1300	1,15	0,45

Wyniki otrzymane w drugiej część ćwiczenia posłużyły mi do przedstawienia graficznie zależności:

I-I
= f(U) dla +U

I-I
= f(U) dla -U

WNIOSKI

Z przeprowadzonego doświadczenia i uzyskanych wykresów można wyciągnąć następujące wnioski. Z badania zależności natężenia prądu fotoogniwa od kąta skręcenia płaszczyzny polaryzacji uzyskałem prawidłowy wykres przedstawiający cosinusoide. Z badania zależności I - I_o w funkcji napięcia przełożonego do fotoogniwa uzyskałam dwa wykresy, z których jeden przedstawia pomiar w wykonany w zakresie od 0 do -1300, a drugi pomiar w zakresie od 0 do +1300 na podstawie wykresów oszacowałem napięcie półfali, które wynosi:

(+) U = 440 [V] ; (-) U = 700 [V]

---