1.Opis położenia punktu w układzie współrzędnych.

Położenie poruszającego sie punktu P w układzie współrzędnych można określić przez x,y,z. Ponieważ współrzędne te SA funkcjami zmiennej t(czasu), to otrzymujemy: Kinematyczne równania ruchu: x=f1(t), y=f2(t), z=f3(t). Równania ruchu w postaci wektorowej |r=|r(t). Jeżeli początek promienia |r pokrywa się z początkiem układu współrzędnych to składowe wektora są równe współrzędnych punktu P. rx=x(t)...Po uwzględnieniu powyższych zależności promień wektora |R możemy zapisać w postaci sumy geometrycznej. |r=|ix(t)+|jy(t)+|kz(t).

2.Definicja prędkości średniej i chwilowej punktu.

Rozpatrujac ruch punktu P w przedziale czasu ∆t=t2-t1, w której punkt przebył drogę ∆s=P1*P2, co można zapisac jako |r2=|r1+∆|r. Stąd prędkość średnia punktu jest ilorazem przyrostu wektora ∆|r w którym ten przyrost nastapil. |V=|r2-|r1/t2-t1=∆|r/∆T. Prędkość chwilowa określa granica przy ∆t dążącym do 0. |V=lim∆t->0 ∆|r/∆t=d|r/dt. Wiedząc, że przyrost ∆|r ma składowe ∆x, ∆y, ∆z stąd: Vx=lim∆t->0 ∆x/∆t=
... Prędkość jest wektorem związanym z poruszającym się punktem |V=
|i+
|j+
|k, którego moduł można zapisać . V=

3. Definicja przyspieszenia punktu materialnego.

Rozpatrując ruch punktu P w przedziale czasu ∆t=t2-t1, w którym wektor prędkości zmienia się z |V1 na |V2, co można zapisać jako |V2=|V1-∆|V. Przyspieszenie średnie punktu wyraża się jako iloraz przyrostu prędkośći ∆|V przez przyrost czasu ∆t. |a=∆|V/∆t. Przyspieszenie chwilowe punktu |a=lim ∆t->0 ∆|V/∆t=d|V/dt=
. Wiedząc, że przyrost prędkośći ∆|V ma składowe ∆|Vx...,stąd składowe wektora przyspieszenia maja postać: ax=lim∆t->0 ∆Vx/∆t=
=
...Przyspieszenie jest wektorem związanym z punktem poruszającym się punktem |a=
|i+
|j...majacym modul a=

4. Ruch prostoliniowy jednostajny i zmienny.

Ruchem prostoliniowym jednostajnym jest ruch punktu po torze prostoliniowym, który odbywa się w takim sposób, że w jednakowych przedialach czasu t punkt przebywa takie same drogi. W tym ruchu droga jest liniową funkcja czasu, zatem: V=ds/dt=const. Czyli ds.=Vdt po scałkowaniu otrzymujemy s=s0+Vt. RYS. Ruch prostoliniowy zmienny jest to ruch punktu po torze prostoliniowym, który odbywa się w taki sposób, że w jednakowych przedziałach czasu t punkt przebywa różne odcinki drogi. Wruchu jednostajnie zmiennym prędkość jest liniowa funkca czasu. A=Dv/dt=const.

5.Ruch krzywoliniowy jednostajny i zmienny- przyspieszenie styczne, normalne.

Ruch krzywoliniowy jednostajny jest to ruch po torze krzywoliniowym l, w którym wektor prędkośći w każdej chwili jest styczny do toru, a jego wartość nie zmienia się z czasem (zmienia się tylko jego kierunek). RYS. Wartość przyspieszenia składowego an prostopadłego do prędkości ma postać an=asinα, an=V²/ro. Składowa przyspieszenia całkowitego w kierunku wektora prędkości at nazywana jest przyspieszeniem stycznym i związana jest ze zmiana wartości wektora prędkości. Wartość at jest określona w postaci: at=acosα at=
. |a=|at+|an. Ruch krzywoliniowy zmienny- jest to ruch punktu po torze krzywoliniowym ruchem niejednostajnym. W tym wypadku wektor prędkośći ruchomego punktu zmienia wartość i kierunek. at≠ 0 an≠0 krzywoliniowy zmienny. at≠0 an=0 prostoliniowy zmienny. at=0 an≠0 jednostajnie krzywoliniowy. at=0 an=0 jednostajnie prostoliniowy.

6.Ruch jednostajny po okręgu - droga, prędkość, przyśpieszenie liniowe i kątowe
Ruch po okręgu jest przykładem ruchu zachodzącego w dwóch wymiarach. Przy którym torem ruchu jest okrąg. Prędkością kątową nazywamy stosunek kąta zakreślonego przez ciało poruszające się po okręgu w
danym czasie do tego czasu. Oznacza się ją symbolem ω. prędkość liniowa, której kierunek jest styczny do okręgu w każdym jego punkcie, jej wartość jest stała. Jest to stosunek przebytej drogi s, do czasu t w jakim ta droga został przebyta. Gdy droga to pełny obwód okręgu, czyli s = 2πr, to czas w jakim została ona przebyta t = T, czyli prędkość liniowa wynosi:
droga kątowa jest to kąt, wyrażony w mierze kątowej (radianach) zakreślony przez promień wodzący obiektu. Promień wodzący, to ten promień, który łączy środek okręgu z aktualnym położeniem obiektu na torze ruchu. Związek między drogą kątową , a drogą liniową jest niezwykle prosty:
. przyspieszenie liniowe jest to stosunek zmiany wektora prędkości Δv do czasu trwania tej zmiany. Przy stałej wartości prędkości, czyli dla ruchu jednostajnego po okręgu, jego wartość wyliczamy z następującego wzoru:
Wektor tego przyspieszenia ma zawsze kierunek promienia wodzącego, a zwrot do środka okręgu. Przyspieszenie kątowe jest to zmiana prędkości kątowej w czasie trwania tej zmiany. W ruchu jednostajnym po okręgu, prędkość kątowa jest stała, czyli przyspieszenie kątowe wynosi 0 (jednostką jest 1 na sekundę do kwadratu)

7.Pojęcie ciała sztywnego.
Ciało sztywne - zbiór punków których wzajemne odległości są stałe.rys. Ruch ciała sztywnego w przestrzeni jest jednoznacznie określony przez równania ruchy trzech punktów, nie lezących na jednej prostej. Aby punkty ABC nie lezaly na jednej prostej musi bys spełniony warunek: (|rb-|ra)x(|rc-|ra)≠0. Ruch ciala sztywnego może być określony wektorowymi równaniami trzech punktów A,B,C. |ra=|ra(t)...Ciało o unieruchomionym 1 punkcie ma 3 stopnie swobody, gdy unieruchomimy 2 punkty ciało ma tylko 1 stopień swobody.rys.

8.Ruch postępowy ciała sztywnego
jest to ruch w którym wszystkie jego punkty doznaja tych samych przesunieć. Ciało w ruchu postępowym ma 3 stopnie swobody.rys. Połozenie punktow A,B,C, poruszającego się ruchem postępowym ciala możemy okreslic za pomoca wektorów: |ra(t0)...w chwili początkowej t0. Następne polożenie ciala odpowiada chwili t=t0+ut czyli upływie czasu ∆t,a polożenie punktów oznaczamy przez A'... Równania ruchu rozpatrywanych punktów mają postać: |ra(t)=|ra(t0)+|u(t)...u(t)- jest przesunieciem jednakowym dla wszystkich punktów ciała. Różniczkujac powyższe równania względem czasu otrzymamy wetrory prędkości A,B,C: |Va=|Vb=|Vc=d|u(t)/dt. Przyspieszenie |aa=|ab=d^2|u(t)/dt.

9.Ruch obrotowy ciała sztywnego wokół nieruchomej osi- prędkość i przyspieszenie.
Bryła może obracać sie jedynie dookoła oosi zwanej osią obrotu. Równanie ma postać ρ= ρ(t). Pierwsza pochodna kata obrotu ρ względem czasu nazywamy prędkością kątową ruchu obrotowego. Prędkość kątowa jest wektorem związanym z osia obrotu którego modul wynosi ω=
, kierunek pokrywa się z osią obrotu a zwrot wynika z reguły śruby prawoskrętnej. Drugą pochodna kąta obrotu, czyli pierwsza pochodna prędkości kątowej nazywamy przyspieszeniem kątowym, Które jest wektorem związanym z osią obrotu o module: ε=
=
. Kierunek tego wektora porusza się z osią obrotu a zwrot jest zgodny ze zwrotem wektora prędkości kątowej gdy obrót jest przyspieszony, przeciwny gdy obrót jest spóźniony.

10. Ruch płaski bryły - pojęcie płaszczyzny kierującej.

Ruchem płaskim ciała sztywnego nazywamy taki ruch, w którym wszystkie punkty ciłą poruszaja się w płaszczyznach równoległych do pewnej płaszczyzny π, zwana płaszczyzna kierujacą. Przez cialo sztywne prowadzimy prostą l prostopadłą do płaszczyzny π. Podczas ruchu bryła prosta l porusza się ruchem postępowym i jest stale prostopadla do plaszczyzny π. Podczas ruchu obrotowego Bryly wokol prostej l punkty leżace na prostej równoleglej do l maja akie same prędkości i przyspieszenia. Ruch płaski jest określony jeśli znamy ruch przekroju bryły po płaszczyźnie kierującej.

11.Równania ruchu płaskiego.

RYS.Układ współrzędnych x,y na płaszczyźnie kierującej. -układ współrzędnych ξ,χ na ruchomym przekroju. |ri - wektor położenia dowolnego punktu P w układzie stałym x,y. - |ρi - wektor położenia punktu P w układzie ruchomym ξ,χ. |ra - wektor położenia bieguna A w układzie stałym. |ri=|ri(t), |ρi=const, α=α(t) - kat ostry miedzy osią x a osiaξ. Położenie układu ruchomego względem układu stałego : xa=xa(t), ya=ya(t), α=α(t). Kinematyczne równania ruchu płaskiego w postaci wektorowej: |ri=|ra+|ρi w skalarnej: xi=xa+ξicosα-χisinα, yi=ya+...Prędkość punktu P przekroju poruszającego się po płaszczyźnie kierującej |
=|
+|
, |
= |Vi- prędkość punktu P przekroju. |
=|Va - prędkość obracanego bieguna A, jednakowa w danej chwili dal wszystkich punktów przekroju. Jest to prędkość ruchu postępowego.

12. Pojęcie ruchu kulistego - określenie położenia bryły.

Ruchem kulistym nazywamy ruch, w czasie którego jeden z punktów bryły jest stale nieruchomy. Ruch kulisty jest obrotem dookoła chwilowej osi obrotu (oś ta zmienia swoje położenie w czasie). Bryła, której jeden punkt jest unieruchomiony ma 3 stopnie swobody. Jej położenie jest opisane w sposób jednoznaczny jedynie za pomocą kątów, zwanych kątami Eulera. Dla określenia tych kątów wprowadzamy układ współrzędnych związanych z bryła ξ - ksi, ζ - dzeta, η - eta. Początkowo osie układu nieruchomego x,y,z pokrywają się z osiami układu ξ , ζ , η. Następnie bryła wykonuje obroty:- wokół osi ξ o kąt
(kąt nutacji), ściśle wokół linii węzłów w. - wokół osi nieruchomej z o kąt ψ(kąt precesji), po wykonaniu tego obrotu oś ξ znajduje się na linii zwanej linią węzłów w.- wokół osi ζ o kąt φ (kąt obrotu własnego). Kolejność wykonywania powyższych obrotów jest dowolna i nie ma wpływu na położenie końcowe bryły.

13. Równania ruchu kulistego bryły - prędkość i przyśpieszenie.

Prędkość. Ponieważ ruch kuli jest obrotem wokół chwilowej osi obrotu, wektor prędkości kątowej leży na tej osi. Wektor prędkości kątowej |ω możemy podać zarówno w nieruchomym układzie osi x,y,z |ω=ωx|i +ωy|j + ωz|k, jak i w układzie związany z bryła |ω=ωξ|eξ+ω η |e η + ω ζ |e ζ. Znając prędkości:
- obrotu własnego,
- precesji oraz
-nutacji, składowe wektora |ω, w układzie ξ , ζ , η obliczamy

15.Zasady dynamiki punktu materialnego.
Dynamika jest działaniem mechaniki opisującym ruch układu materialnego pod wpływem sil działających na ten układ. -Punkt materialny na który nie działają żadne sily lub działają sily które się wzajemnie równoważą pozostaje względem układu odniesienia w spoczynku lub ruchu jednostajnie prostoliniowego. - zmiana ilości ruchu (pędu) jest proporcjonalna względem sily działającej i Mia kierunek prostej wzdłuż ktorej ta sila dziala. - akcja i reakcja - każdemu dzialaniu towarzyszy rowne lecz przeciwne zwracanie oddziaływania .- prawo super pozycji - jeśli na punkt materialny o masie M dziala jednoczesnie kilka sil to punkt uzyskuje przyspieszenie równe sumie geometrycznej przyspieszen jakie uzyskaly by w wyniki niezdolnego dzialania każdej z sil.- kazde dwa punkty materialne przyciągają się wzajemnie z sila wprost proporcjonalna do iloczynu mas (m1m2) odwrotnie proporcjonalne do kwadratu odległości(r) miedzy nimi, kierunek sily lezacej na prostej łączącej te punkty.

16.Siła bezwładności - zasada d'Alamberta.
Siła bezwładności jest równa iloczynowi masy przez przyspieszenie ruchu jej kierunek jest taki jak kierunek przyspieszenia ruchu jej zwrot jest zas przeciwny niż zwrot przyspieszenia. Siła bezwładności jest =0 wtedy gdy w ruchu nie wystepuje przyspieszenie. Szczegolnosci styczna sila bezwładności nie wystepuje w ruchu jednostajnym punktu, normalna sila bezwładności jest =0 w ruchu prostoliniowym. Zasada-w ruchu swobodnym punktu materialnego układu sil czynnych równoważy się z sila bezwładności [Ε|Fi+(-m|a)=|0]. W ruchu punktu nie swobodnego sily czynne i reakcje więzów równoważą się z sila bezwładności [Ε|Fi+Ε|Ri+(-m|a)=|0].

17.Zasada pedu masy impulsu sily punktu materialnego.
Punkt materialny o masie M porusza się pod wpływem układu sily |F1,|F2,...|Fn, Druga zasade możemy zapisac w postaci d/dt(m|v)=Ε|Fi, Wektor |p=m|v nazwywamy pedem lub ilością ruchu punktu materialnego. Zasada pedu -|p=Ε|Fi. Pochodna pedu punktu materialnego względem czasu jest rowna sumi sily działających na dany punkt. W przypadku gdzy na punkt materialny nie działają silu lub sily równoważą się ped punktu materialnego jest staly. |p= const. Przypisujac 2 zasade Newtona w postaci |Fdt=d(m|v).Zdj. przyrost masy poruszającego się punktu jest rowny impulsowi całkowitemu sil działających. Wniosek. Dla zmiany pedu masy niezbędny jest określony jest czas działania siły. Z równania tego wynika ze zmiana wektora pedu będzie tym intensywniejsza, im wieksza będzie siła |k oraz im wieksza będzie masa i ped początkowy |p.

18.Zasada krętu punktu materialnego.
Po dowolnym torze porusza się punkt o masie M z prędkością |v. Obierajac dowolny punkt 0 jako poczatek układu stalego x,y,z i łącząc go z poruszającym się punktem promieniem-wektorem|r.RYS.Kretem poruszającego się punktu materialnego względem danego bieguna 0 nazywamy wektor rowny iloczynowi wektorowemu promienia przez pęd poruszającego punktu. Kręt jest więc momentem pedu względem obranego bieguna. Po zróżniczkowaniu wektora kretu względem czasu. d|k/dt=d|r/dt x m|v+|r x d/dt(m|v) czyli |k=|v x m|v +|r x m|a. Pochodne wektora krętu względem czasu jest rowna momentowi głównemu wszystkich sil działających na dany punkt materialny.[|k=|M] . Jeżeli moment sil działających na poruszajacy się punkt materialny jest względem jakiegos bieguna =0 to kręt poruszającego się punkty względem tego bieguna jest wektorem stalym |M = |0 =|k = const.

19.Dynamiczne równania punktu materialnego.

Dynamiczne rownanie ruchu |F=m|a uwzglednia zmiane zależności |F=|Fxi+|Fyj+|Fzk, |a=
|i+
|j+
|k. Dynamiczne rownanie ruchu można zastąpić 3 rownaniami analitycznym. Fx=m
, Fy=m
, Fz=m
. W biegunowym układzie współrzędnych dynamiczne równania ruchu maja postać m(
-r
²)=Fr, md/rdt*(r²
)=Fρ. W układzie współrzędnych równania te będą wyglądały następująco m(
-r
²)=Fr, md/rdt*(r²
)=Fρ, m
=Fz. W naturalnym układzie współrzędnych mdv/dt=Ft,m=V²/r=Fn, ma_b=F_b=0.

21. Drgania swobodne i tłumione punktu materialnego.

Ruchem drgającym punktu materialnego (drganiem) nazywamy ruch w dostatecznie małym  otoczeniu położenia swojej równowagi stałej tego punktu. Jeżeli punkt materialny zostanie wychylony z położenia równowagi, to zostaną wywołane drgania tego punktu. Ruchem punktu materialnego, na który działa siła
 proporcjonalna do tego wychylenia od pewnego nieruchomego punktu
 i skierowana w stronę tego punktu. Rozpatrzymy przypadek, gdy punkt materialny porusza się po linii prostej, na której leży również wspomniany wyżej punkt
. Jeżeli tę prostą obierzemy jako oś
z początkiem w punkcie
, a współczynnik proporcjonalności między siłą przyciągającą a wychyleniem punktu materialnego oznaczmy symbolem
, to równanie różniczkowe ruchu będzie miało postać:

                                        
Znak minus po prawej stronie powyższego równania pochodzi stąd, iż dla
 siła
 ma zwrot przeciwny do osi
, a dla
 siła ta ma zwrot zgodny z osią. Przenosząc w równaniu tym wyraz
 na lewą stronę mamy:  
   Drgania swobodne - drgania zachodzące pod działaniem sił sprężystych. Tłumione. Obecnie założymy, że na punkt materialny działa, oprócz siły
proporcjonalnej do wychylenia, jeszcze siła oporu
, której wartość jest wprost proporcjonalna do prędkości.
przy czym
odpowiada położeniu równowagi.  Wprowadzając oznaczenia

    
,równanie można napisać w postaci:
  

22. Drgania wymuszone punktu materialnego - rezonans mechaniczny

Drgania wymuszone nietłumione

   Zakładamy, że oprócz siły
, proporcjonalnej do wychylenia, na punkt materialny działa jeszcze pewna siła
, której wartość jest okresową funkcją czasu, przy czym: 
     

Równanie różniczkowe ruchu przybierze teraz postać:

                                                         
albo 

Drgania wymyszone tłumione

    Zbadamy teraz wpływ  tłumienia na drgania wymuszone. Jeżeli oprócz sił 
  i  
na punkt materialny działać będzie jeszcze siła 
, której wartość jest okresową funkcją czasu, przy czym
,  to równanie różniczkowe ruchu ma postać : 
 

  Albo, stosując oznaczenia , postać : 

23.Ruch punktu materialnego po gładkiej równi pochyłej.

Równania ruchu:

Po przekształceniu otrzymujemy:

24.Ruch wahadła matematycznego.

Równania ruchu:

gdzie:

Po podstawieniu:

Dla niewielkiego kąta ၪ mamy sinၪ ≈ ၪ , więc: zatem

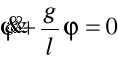
więc równanie ruchu przybiera postać:

Jest to równanie ruchu harmonicznego prostego.

Przypomnijmy, że równanie ruchu harmonicznego prostego ma postać:

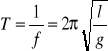
Zatem dla wahadła:

Załóżmy, że dla t = 0, wówczas

Równanie ruchu ma postać:

Po scałkowaniu względem czasu otrzymamy wzór na prędkość:

Warunek początkowy: dla

Po wyznaczeniu stałej c i podstawieniu do wzoru na v

25.Zderzenie proste i ukośne ciał.

Zderzenie zachodzi w przypadku działania na siebie dwu ciał siłą o skończonej wartości w bardzo krótkim przedziale czasu. Zderzenie środkowe charakteryzuje się tym, że normalna do płaszczyzny styku w punkcie styku obu ciał przechodzi przez środki masy tych ciał.

W procesie zderzenia rozróżniamy dwa charakterystyczne okresy:

- pierwszy okres: od chwili zetknięcia się ciał aż do chwili największego zbliżenia ich środków mas, przy równoczesnym odkształcaniu się obu ciał, - drugi okres: od chwili rozpoczęcia oddzielania się obu mas. Pęd przed i po zderzeniu jest taki sam.

c- wspólna prędkość obu mas przy końcu pierwszego okresu.

współczynnik restytucji
Wartości graniczne współczynnika k odpowiadają: dla ciała idealnie sprężystego k=1 dla ciała idealnie plastycznego. k=0

Ukośne. Rozkładamy wektory prędkości na składowe normalne i styczne do płaszczyzny styku

Jeżeli pominiemy straty tarcia przy zderzeniu i możliwości ewentualnych obrotów mas, to składowe styczne w wyniku zderzenia nie ulegną zmianie, zmienią się tylko składowe normalne.

28.Kręt układu punktów materialnych.

Kręt układu punktów materialnych względem dowolnego punktu 0 (bieguna), jest to wektor równy sumie geometrycznej krętów wszystkich punktów materialnych układu względem bieguna.

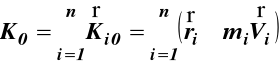
Wartości rzutów wektora krętu K₀ na osie xyz są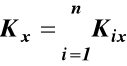


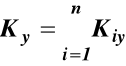
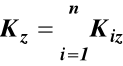
Pochodna krętu ma postać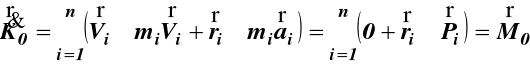
Jeśli M₀ = 0 to K₀ = const Pochodna względem czasu krętu punktów materialnych względem dowolnego punktu 0 równa jest sumie geometrycznej momentów sił zewnętrznych, jeżeli punktem 0 jest punkt nieruchomy lub środek masy układu C.

30. Definicja i równania pracy mechanicznej sily stałej.

Pracę siły stałej na prostoliniowym przemieszczeniu w kierunku działania sily nazwywamy iloczynem tej sily przez długość przesuniecia A=Fs I=Nm=kgm²/s². Rys. jeżeli wektor jest nachylony do kierunku przesuniecia pod katem α, to prace obliczamy ze wzoru A=F_ts=Fscosα, ponieważ prace wykonuje tylko skladowa sily stycznej do toru F_t. Praca składowej normalnej do toru F_n =0. α=0 -A=Fs>0, 0<α<90- A=Fscosα>0, 90<α<180 - A=Fscosα<0, α=180- A=-Fs<0, α=90 -A=0. Praca jest skalarem, Praca może przyjmowac wartości dodatnie ujemne i =0, prace wykonuje jedynie skladowa sily stycznej do toru.

31.Praca mechanicznej sily zmiennej.

Prace elementarna sily zmiennej na przesuniecie d|s nazywamy iloczynem skalarnym sily |F przez to przesuniecie elementarne. δA=|F*d|s. Ponieważ |F*d|s= Fds cos(|F, d|s) = Ftds zatem δA=Ftds. Parca sily na pewnym przesunieciu jest rowna sumie prac sil składowych na odpowiednich przemieszczeczniach składowych. Prace całkowita od położenia od 1 do 2 na torze otrzymamy całkując wyrazenie przedstawiające prace elementarna.Rys.

33.Praca mechaniczna sily sprężystości.

Siła sprężystości |s jest wielkością zmienna proporcjonalna do wydłużenia sprężyny. Przyjmujac os sprężyny za os x napiszemy: S=cx c-stala sprężyny, Praca elementarna sily sprężystości jest rowna δA=xdx+ydy+zdz. Składowe sily sprężystości x=-s , y=0 z=0. Po podstawieniu δA=-cxdx. Praca całkowita sily sprężystości na drodze całkowitego wydłużenia sprężyny będzie rowna A=-
=-cl²/2, uwzględniając że cl=s, A=-1/2sl.

34. Praca mechaniczna sily ciężkości.

Praca elementarna δa= xdx+ydy+zdz, składowe sily ciężkości x=0 y=0 z=-mg, zatem praca elementarna δA= -mgdz. Praca całkowita A=-
.

35. moc i sprawność układu.

Prace odniesienia do jednostki czasu nazywamy moca, moc calkowita P=δA/dt, wyrazenie na moc chwilowa przestawic można w następującej postaci P=Ftds/dt lub P=FtV. W ruchu obrotowym P=ndρ/dt ponieważ dρ/dt=ω dlatego P=Moω. Gdy prednosc w ruchu obrotowym zadana jest za pomoca prędkości obrotowej n(Obr/min) wówczas prędkość Katową ω obliczamy ze wzoru. ω=πn/30. Po podstawieniu do π=nω mamy P = Mo πn/30. Jednostka mocy W=I/s=Nm/s (kW,MW). Sprawnoscia mechaniczna maszyny lub silnika nazywamy stosunek pracy (lub mocy) użytecznej do pracy (lub masy) włożonej. η=Au/A= Pu/P.

36.Zasda zachowania pracy i energi kinetycznej.

Przy wyrażeniu sily Ft w postaci Ft=mat =mdv/dt. Wzor na prace przybiera postac δA= Ftds=mdvds(ds=Vdv)/dt=mVdv=δE (E=mV²/2 ). Prawa strona tego rownanie jest rozniczka zupelna funcji E=mv2/2 zwanej energia kinettyczna poruszającego się punktu materialnego, zatem δA=dE po calkowaniu otrzymujemy A1-2 = E2-E1. Energia kinetyczna poruszającego się punktu materialnego rosnie lub maleje, wielkość pracy wykonanej przez sily działające na ten punkt materialny.

37.Praca w polu sił.

Prace calkowita wykonana przez sily pola okresla całka. A1-2=
, aby obliczyc prace calkowita należy ustalic a) wposlrzedne punktu początkowego i koncowego b) wektor sily pola |F=|F(x,y,z) takie pola sily w których praca zalezy od kształtu toru nazywamy polami niepotencjalnymi lub wirowymi. w polu potencjalnym praca nie zalezy od ksztalu toru a jedynie od położenia pozcatkowego i koncowego sily pola - = wartości funkcji i pola w położeniu koncowym i początkowym.

38.Potencjal pola sil.

Okreslic pole sily tzn. podac wektor funkcje położenia |F=|F(x,y,z) albo jego składowe x=x(xyz), y=y(xyz), z=z(xyz). Lienie charakteryzujaca się tym ze w każdym jej punkcie wektor pola jest styczny do niej, nazywamy linia pola sil. Rownanie rozniczowe tych lin ma postac dx/x+dy/y=dz/z. Jeżeli linie pola sil są prostymi równoległymi pole nazywamy jednorodnym. Funkcją pola sil nazywamy funkcję położenia φ(x,y,z) której rozniczka zupelna jest rowna pracy elementarnej sil pola.

39.Zasada zachowania energii mechanicznej.

Pracę 0=mgh nazywamy energia potencjalna. Jest to praca jaka wykona pole sil ciężkości przy przemieszczaniu masy z wysokości h na powierzchnie ziemi. E+V= const. W polu potencjalnym suma energi kinetycznej i potencjalnym jest w każdym położeniu wielkscia stala. W odniesieniu do poruszającego się punktu zasade te możemy przedstawic mv2/2+mgh=const. Z zasady pracy i energii kinetycznej δA= dE oraz z pracy i energii potencjalnej δA=-dV, wynika że dE=-dV czyli dE+Dv=0 - forma różniczkowania do zachowania energii mechanicznej.

40.Równowaga punktu w polu sil ciężkości.

Równowage punktu w polu ciężkości na gładkim torze |F+|R=0. Punkt będzie w równowadze na krzywej gładkiej wtedy gdy wypadkowa sil czynnych będzie prostopadla do tej krzywej. W polu sil ciężkości rownowaga punktu materialnego w położeniu, gdzie energia potencjalna osiaga ekstremum(rys). w szczególności rownowaga stala zachodzi w położeniu w którym energia potencjalna osiaga minimum. Jest to tak zwane kryterium statyczności Minidinga i Diriechleta.

---