Stany nieustalone w obwodach elektrycznych

1.Podstawy teoretyczne

Włączenie stałego napięcia do obwodów RL, RC lub RLC jest równoznaczne z pobudzeniem układu skokiem jednostkowym, którego przebieg pokazano na rysunku 10.

Rys.1. Przebieg funkcji skokowej

Zjawiska zachodzące przy przejściu układu z pewnego stanu ustalonego w inny, również ustalony, nazywamy stanem nieustalonym. Może on być spowodowany np. włączeniem źródeł elektrycznych, zmianami w konstrukcji obwodu (przełączenia) lub zmianami jego elementów

Zmiany parametru lub konfiguracji obwodu występujące w określonej chwili nazywamy komutacja. Elementy L i C mają zdolność magazynowania energii odpowiednio w polu magnetycznym i elektrycznym obowiązuje wiec dla nich zasada zachowania energii (ciągłości zmian), z której wynikają tzw. prawa komutacji:

a) zasada ciągłości strumienia w cewce

co przy założeniu liniowości L prowadzi do zależności:

gdzie:

- prąd w chwili poprzedzającej chwilę początkową t = 0,

- prąd w chwili następującej po chwili początkowej t = 0,

b) zasada ciągłości ładunku na kondensatorze
:

co przy założeniu liniowości C prowadzi do zależności:

gdzie:

- napięcie w chwili poprzedzającej chwilę początkową t = 0,

- napięcie w chwili następującej po chwili początkowej t = 0.

1.1.Włączanie stałego napięcia do obwodu składającego się z elementów RL połączonych szeregowo

Przeanalizujemy zjawiska występujące podczas włączania napięcia stałego do obwodów elektrycznych zawierających elementy R,L i C. Włączanie napięcia stałego do obwodu składającego się z elementów RL połączonych szeregowo. Określmy przebieg zmian prądu i oraz, napięcia u_L, w obwodzie przedstawionym na rysunku 2.

Rys.2 Gałąź szeregowa RL zasilana napięciem stałym

Z bilansu napięć chwilowych w oczku otrzymujemy:

(1)

Do rozwiązywania równań różniczkowo-całkowych wygodnie jest zastosować rachunek operatorowy, który daje ostatecznie równania algebraiczne, jest to dużym uproszczeniem, szczególnie w przypadku rozwiązywania układów równań różniczkowych.

Równanie (1) po przekształceniu Laplace'a przyjmuje postać:

(2)

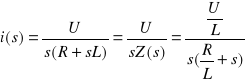
(3)

gdzie:

- impedancja operatorowa obwodu.

Wykonując odwrotne przekształcenie Laplace'a z równania (3) otrzymamy:

(4)

Wartość chwilowa napięcia u_L będzie równa:

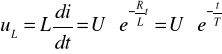
(5)

- stała czasowa.

Pojecie stała czasowa odpowiada czasowi, po którym układ osiągnąłby stan ustalony, gdyby prędkość zmian, np. napięcia, była stała i równa prędkości zmian dla t = 0.

Ze wzorów (4) i (5) wynika, że po czasie t = T prąd osiąga wartość
a napięcie
. Spostrzeżenie to pozwala na graficzne wyznaczenie wartości stałej czasowej (rys.3).

Rys.3. Przebiegi prądu oraz napięcia u_L po włączeniu napięcia stałego dla obwodu RL

1.2.Włączanie stałego napięcia do obwodu składającego się z elementów RC połączonych szeregowo.

Przeanalizujemy przebieg zmian napięcia oraz prąd ładowania kondensatora i w obwodzie przedstawionym na rysunku 4.

Rys.4. Gałąź szeregowa RC zasilana napięciem stałym

Z bilansu napięć chwilowych w oczka otrzymamy:

(6)

gdzie:

(7)

Równanie (6) po przekształceniu Laplace'a przyjmie postać:

(8)

czyli:

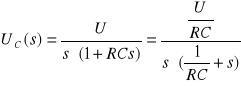
(9)

stąd wartość chwilowa napięcia wynosi:

(10)

a wartość chwilowa prądu

(11)

gdzie:

- stała czasowa.

Przebieg napięcia u_C oraz prądu ładowania i przedstawia rysunek 5.

Rys.5.5. Przebiegi napięcia u_C oraz prądu i po włączeniu stałego napięcia do szeregowego obwodu RC

1.3.Włączanie stałego napięcia do obwodu składającego się z elementów RLC połączonych szeregowo.

Określmy przebieg zmian prądu w obwodzie przedstawionym na rysunku 6.

Rys.6. Gałąź szeregowa RLC zasilana stałym napięciem

Prąd można wyznaczyć wg wzoru (12):

(12)

gdzie:

stąd:

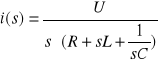
lub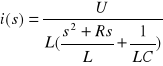
(13)

Równanie
jest równaniem drugiego stopnia. Funkcja i(s) posiada dwa bieguny: s₁ i s₂

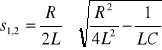
(14)

a)
, wówczas dwa bieguny s _1,2 są rzeczywiste i wynoszą:

(15)

gdzie:

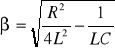
Wartość chwilowa prądu w takim przypadku jest równa:

(16)

Przebieg prądu i(t) jest przedstawiony na rysunku 7.

Rys.7. Przebieg prądu i(t) w szeregowym obwodzie RLC, w przypadku gdy

b)
; wtedy
i bieguny:
, a wartość chwilowa prądu jest równa:

(17)

przebieg i(t) ilustruje rysunek 8.

Rys.8. Przebieg prądu w szeregowym obwodzie RLC, w przypadku gdy

c)
; wówczas bieguny s₁ oraz s₂ tworzą parę sprzężoną zespoloną:

;

gdzie:

,
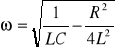
(18)

Wartość chwilowa prądu jest wówczas równa:

(19)

Przebieg prądu i(t) przedstawia rysunek 9.

Rys.9. Przebieg prądu i(t) w szeregowym obwodzie RLC, w przypadku gdy

i(t) i(t)

u(t)=U1(t)

U

t

u(t)

e^-αt

U

u_C(t)

C

R

i(t)

U

0

i(t)

i(t)

R L C

u(t)

t

u_L (t)

L

R

i(t) i(t)

---