Zadanie 1

Do doprowadzenia wody do punktu odbioru służy instalacja hydroforowa, która podaję wodę o lepkości ν =1,3x10^-6 m²/s na wysokość h=35 m. Rurociąg ma śred. D=50 mm i długość L=50m.Wsp.tarcia λ=0,025, wsp. oporów miejscowych wynoszą odpowiednio: wlot do przewodu ξ₁=0,5,zawór grzybkowy ξ₂=4,8,dwa kolana ξ₃=2x0,51=1,02.Nadciśnienie powietrza nad zwierciadłem wody w zbiorniku hydrofor. wynosi [₁=4x10⁵ Pa. Obliczyć strumień objętości V podawanej wody.

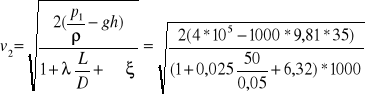
v₂ = 1,87 m/s

Zadanie 2

Ze zbiornika o dużych wymiarach wypływa woda przez rurociąg ,jak na rys. Obliczyć strumień wody V, jeżeli rurociąg ma średnicę D=80mm i długość L=200m. Różnic poziomów wody wynosi h=8m.Wsp. strat mają wartość λ=0,02-tarcie,ξ_w=0,5-wlot do rurociągu, ξ_k=0,15-kolano.

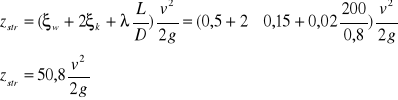
Zadanie 3

Na przewodzie o średnicy d₁ =20mm doprowadzającym wodę do zbiornika zainstalowano dyfuzor o średnicy wylotowej d₂=50mm i kącie 2α=8⁰. O ile zwiększy się wysokość podnoszenia h w porównaniu do poprzedniego stanu, tzn. gdy wodę doprowadzano do zbiornika bez pośrednictwa dyfuzora? Strumień objętości wody wynosi

V=1,5·10^-3m³/s

W przypadku istnienia dyfuzora:

h_str=ζ ∙ (V₁²/2g) + (V₂²/2g )

h_str-strata w dyfuzorze;

ζ-str. wlotu do zbiornika.

Dla 2α=8→

ζ=k[1-(d₁/d₂)²]²=0,15∙[1-(20/50)²]²= 0,106

Prędk.V₁=V∙(πd₁²/4) = (4·1,5·10^-3) / ( Π∙0,02²)= 4,78m/s

V₂=V₁∙(d₁/d₂)²=4,78∙(20/50)²=0,76m/s

h_str=0,106·(4,78²/2·9,81)+(0,76²/2·9,81)= 0,153m

Gdy brak dyfuzora strata doprowadzenia wody do zbiornika: h_str=V₁²/2g=4,78²/2·9,81=1,16m

→ zainst.właśc.dyfuzora(2α=8) umożliwia zmniejszenie strat i uzyskanie zwiększonej wys. podnoszenia

Δh=1,16-0,153=1m

Zadanie 4

Pompa wirnikowa przepompowuje wodę ze studni do zbiornika na wieży ciśnień. Obliczyć moc P pompy i ciśnienie p₂ przed pompą (ciśnienie ssania) gdy strumień objęt. wody V=0,71·10^-3m³/s, współ. lepkości kinematycznej wody w temp.20⁰C ν=1∙10^-6m²/s, średnica przewodu D=30mm. Długości poszczególnych odcinków przewodu: H₀=3m, H₁=2m, H₂=8m, H₃=0,5m, L₁=27m, L₂=50m, L₃=1m. Sprawność pompy η=0,6, współ. oporów miejscowych: ssawki ζ₁=5 i kolan ζ₂=0,33.

Re=1·0,03/10^-6 = 30000-turbulentny charakter przepływu.

Współczynnik tarcia wynika ze wzoru Blasiusa:

λ=0,3164/
= 0,3164/
=0,0131.

Całkowita wys. H pompowania:

H=H₁+H₂+H₃+V²/2g·[1+ζ₁+3ζ₂+ λ(H₀+H₁+H₂+L₁+L₂)/D]=

=2+8+0,5+1²·[1+5+3· 0,33 +0,0131·(3+2+8+27+50)/0,03]/2·9,81= 12,9m.

Moc silnika napędzającego pompę

P=ρgVH/η=(9,81·1000·0,71·10^-3·12,9)/0,6=150W =0,15kW

Bezwzględne ciś.p₂ przed pompą (przekrój 2) z równania Bernoulliego dla przekrojów 1 i 2:

p_a/ρg+H₀ = p₂/ρg+H₀+ H₁+V²/2g[1+ζ₁+ζ₂+λ(H₀+H₁+L₃)/D]

Przyjęto p_a=1∙10⁵Pa

p₂=p_a-ρg[H₁+V²/2g·(1+ζ₁+ζ₂+ λ(H₀+H₁+L₃)/D]=

10⁵-1000·9,81[2+(1+5+0,33+ 0,0131·(3+2+1)/ 0,03)]/(2·9,81)=75905Pa.

Zadanie 5

Anemometr o promieniu wirnika R służy do pomiaru prędkości powietrza v_∞,obraca się ze stałą prędkością kątową ω.Obliczyć prędkość v_∞, przy założeniu, że na czasze działają tylko siły oporu aerodynamicznego.

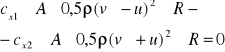
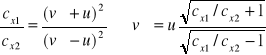
Zadanie 6

Kula stalowa o średnicy d=20mm i ρ_k=7800kg/m³ opada w zbiorniku wypełnionym olejem o gęstości ρ_o=850kg/m³ i współczynniku lepkości kinematycznej v=0,37*10^-4 m²/s. Wyznaczyć jednostkową prędkość opadania kuli v_∞.

Siła ciężkości i wyporu

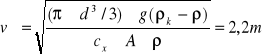
Zadanie 7

W rotametrze wodnym ustalił się stan równowagi pokazany na rys. tj. pływak wzniósł się na wysokość h_w, której odpowiada średnica wewnętrzna szklanej rury rotametru D=34mm. Dane pływaka: objętość V_p=4,4cm³,średnica d=20mm,gęstość materiału ρ_p=7850kg/m³ ,wsp. oporu c_x=1,0 dla R_e>1x10⁴.Przyjąć wsp. lepkości kinematycznej wody v=1,11*10^-6 m²/s. Obliczyć strumień objętości wody V.

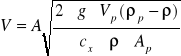
Powierzchnia wolnego przekroju pierścienia

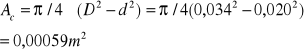
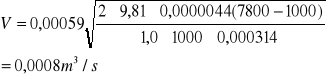
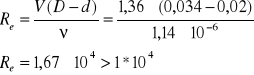
Zadanie 8

Przewód zakrzywiony jest zaopatrzony w otwór wylotowy o pow. Przekroju A=80cm². Środek geometryczny otworu znajduje się na głębokości h=0,4m pod zwierciadłem wody. Obliczyć moc P poziomej reakcji R, wywieranej przez wypływającą ciecz z przewodu poruszającego się z prędkością unoszenia u. Przy jakiej prędkości unoszenia moc osiągnie największą wartośc? Jaka jest zależność mocy od prędkości unoszenia? Pominąć opory ruchu.

Prędkośc wypływu wody (prędkość względna) wynika ze wzoru Torricellego

Strumień objętości wypływającej wody:

Reakcja R i moc P wynoszą odpowiednio:

Aby obliczyć maksymalną moc, należy zróżniczkować ostatnie równanie względem u i przyrównać do zera. Otrzymuje się:

stąd

Moc maksymalna wynosi:

Zależność mocy od prędkości unoszenia:

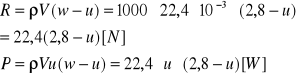
Zadanie 9

Koło Segnera składające się z 2 (i=2) zagiętych rurek o średnicy d=8mm służy do rozpryskiwania wody. Obliczyć moc P dostarczoną do koła o promieniu r=0,6m wirującego z częstością obrotów n=120 obr/min, jeżeli ogólny strumień objętości wody wynosi V=60dm³/min.

Reakcja wypływającej wody wynosi:

m-masa strumienia

V-prędkość z jaką ta woda się przemieszcza

Strumień masy wypływającej z jednej rurki ma wartość:

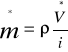
V-prędkość bezwzględna rozpryskiwanej wody

u-prędkość obrotowa rurek

Prędkość wypływu wody z rurek wynosi

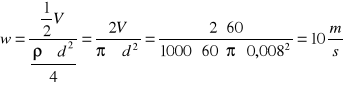
Moment obrotowy:

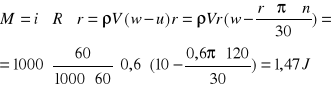
Moc dostarczana do koła bez uwzględniania strat ma wartość:

Zadanie 10

Obliczyć max. wysokość ssania h pompy wirnikowej, jeżeli ciśnienie wody na wlocie do pompy ma być wyższe o Δp=100hPa od ciśnienia wrzenia wody p_w. Pompa wirnikowa zasysa wodę o temp.60⁰C w ilości ύ=0,06m³/s rurociągiem o średnicy d=20mm i dł.L=6m. Uwzględnć tylko opory tarcia. Przyjąć współ. tarcia λ=0,02.

Rów. Bernoulliego dla swobodnej pow. wody 1 i dla wlotu do pompy2 ma postać:

p_a=ρv²/2+p₂+ρgh+p_str

Przyjęto p_a=1000hPa= 100 000Pa

Ciśnienie wody na wlocie do pompy:

p₂=p_w+Δp= 200+100=300hPa=30000Pa

z tabl.D20 przyjęto ciśnienie wrzenia wody p_w=200 hPa

Nadwyżka ciśnienia Δp ma zabezpieczyć pompę przed wystąpieniem zjawiska kawitacji.

Prędkość wody w rurociągu:

v=4V/πd²=(4·0,06) / (60·π·0,02²)= 3,18m/s

p_str=λlpv²/2d = 0,02·6·1000·3,18²/(0,02·2)= 30400Pa

34543,8=98104h h=3,53m

h=(p_a-p_str-p₂-ρV²/2)/ρg =(100000-30400-3000-1000·3,18²/2)/ 9,81·10000=3,53m.

Zadanie 11

Silnik strumieniowy porusz się z prędkościa u=900km/h.

Obliczyć siłę ciągu i moc silnika, jeżeli strumień masy spalin wynosi m=15kg/s, a prędkość wypływu spalin z dyszy w=870m/s.

Siła ciągu silnika(reakcja strugi):

Moc silnika:

Zadanie 12

Statek ma napęd w postaci odrzutowej dyszy wodnej, która jest zasilana pompą zasysającą wodę z otoczenia. Woda wypływa przez dyszę o powierzchni przekroju A z prędkością v względem dyszy. Obliczyc teoretyczną i max. sprawność napędu jeśli prędkość statku wynosi u.

Ruch statku wywołany jest reakcją R:

Strumień masy wody wypływającej z dyszy:

Prędkość bezwzględna wypływu wody z dyszy

Moc użyteczna statku:

Moc dostarczona do wody wypływającej z dyszy:

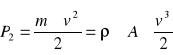
Zadanie 13

Płyta mogąca się obracać dookoła osi poziomej O jest podtrzymywana przez pionowa strugę wody wypływającą z prędkością v₁=15m/s z rury o średnicy d=20mm. Obliczyć ciężar płyty G jeżeli b=500mm,a=350mm,z=2m. Pominąć opór powietrza lecz uwzględnić działanie przyspieszenia ziemskiego na strugę.

Z równania Bernouliego wynika prędkość strugi v₂ przy zetknięciu się z płytą:

Z równania ciągłości przepływu strumień masy wody: