Politechnika Zielonogórska Zakład Fizyki Technicznej	Sprawozdanie z ćwiczenia: Temat: Wyznaczenie przyspieszenia ziemskiego, przy pomocy wahadła rewersyjnego
Marek Gaweł gr. 34 A Wydz. Mechaniczny	Data: 13.03 2000 Nr ćw.: 2	Zaliczenie:

Obowiązujący zakres materiału:

1. Drgania oscylatora harmonicznego

1. niegasnące

2. tłumione

3. wymuszone

2) Wahadła jako przykład ruchu harmonicznego

1. wahadło matematyczne

2. wahadło fizyczne - grawitacyjne, środek wahań, długość zredukowana

3) Wykorzystanie właściwości środka wahań w konstrukcji wahadła rewersyjnego

4) Przyspieszenie ziemskie i jego zależności od odległości od środka ziemi i współrzędnych geograficznych

Literatura:

1. M. Skorko - „Fizyka”

2. Cz. Bobrowski - „Fizyka - krótki kurs”

3. J. Massalski, M. Massalski - „Fizyka dla inżynierów tom I”

4. Słownik fizyczny

5. T. Dryński - „Ćwiczenia laboratoryjne z fizyki”

I.WSTĘP TEORETYCZNY

1. Drgania oscylatora harmonicznego

Ruch, który powtarza się w regularnych odstępach czasu, nazywamy ruchem okresowym (periodycznym). Przemieszczenie cząstki w ruchu periodycznym można wyrazić przy pomocy funkcji sinus i cosinus. Ponieważ funkcje te nazywamy funkcjami harmonicznymi - ruch periodyczny często nazywany jest ruchem harmonicznym złożonym, lub krótko ruchem harmonicznym. Okresem ruchu harmonicznego T jest czas trwania jednego pełnego drgnięcia lub cyklu. Częstością ruchu u jest liczba drgań przypadających na jednostkę czasu. Zatem częstość jest po prostu odwrotnością okresu:

Jednostką częstości w układzie SI jest jeden cykl na sekundę albo jeden herc (Hz). Częstość można opisać jeszcze jednym wzorem :

gdzie stała ω jest zwana pulsacją lub inaczej częstością kątową. W układzie SI jednostką pulsacji jest radian na sekundę (rad/s). Położeniem równowagi w ruchu drgającym nazywamy położenie, w którym na punkt materialny nie działa siała wypadkowa. Przemieszczenie (wychylenie) jest to odległość drgającego punktu materialnego od położenia równowagi w dowolnej chwili. Zatem drgania harmoniczne pewnej wielkości fizycznej x można opisać równaniem postaci :

gdzie :ω, A - są wielkościami stałymi, tzn. nie zależne od czasu

t - to czas w sekundach (s).

Znaczenie stałej A wynika z charakteru funkcji sinus - funkcja ta może się zmieniać
w granicach od -1 do 1. Stąd punkt drgający może się odsuwać od położenia równowagi najdalej o +A lub -A. Stała A oznacza więc największe wychylenie od położenia równowagi. Drgania dokoła położenia równowagi odbywające się zgodnie z powyższym równaniem nazywamy często oscylacjami harmonicznymi, a ciało wykonujące takie drgania - oscylatorem harmonicznym. Drgania oscylatora harmonicznego możemy podzielić na niegasnące, tłumione oraz wymuszone.

1. drgania niegasnące

Są to drgania o stałej amplitudzie A i niezmiennej energii całkowitej E_c. Prędkość v
w ruchu harmonicznym opisujemy :

Prędkość jest wielkością zmienną, okresową - jej największa wartość wynosi v_max=Aω''.
W analogiczny sposób można wyznaczyć przyspieszenie :

a iloczyn Asinωt wyraża wychylenie x a zatem :.

Stąd wynika, że przyspieszenie w ruchu harmonicznym jest proporcjonalne do wychylenia od położenia równowagi. Znak minus w tym wzorze mówi nam, że zwrot przyspieszenia jest zawsze przeciwny do zwrotu wychylenia od położenia równowagi.

Gdyby jednak ciało w chwili początkowej nie znajdowało się w położeniu równowagi wówczas wychylenie opisuje się równaniem :

Wartość kąta w nazywamy fazą początkową ruchu harmonicznego, podczas gdy całość wyrażenia (ωt + ϕ ) nazywamy fazą ruchu harmonicznego lub fazą drgań. Z punktu widzenia dynamiki wynika, że punkt materialny o masie m, wykonujący ruch harmoniczny podlega działaniu siły F wyrażonej :

Siła ta jest proporcjonalna do wychylenia i przeciwnie do niego skierowana. Współczynnik proporcjonalności mω ² = k nazywany jest zwykle współczynnikiem sprężystości. Uwzględniając drugą zasadę dynamiki można to równanie napisać w postaci :

Całość rozważań dotyczących ruchu harmonicznego można oprzeć na tym równaniu jako równaniu wyjściowym definiującym badany ruch.

b) drgania tłumione.

Drgania odbywane w warunkach rzeczywistych, w dowolnym ośrodku materialnym, zawsze są połączone z przekazywaniem energii otoczeniu w związku z pokonywaniem sił oporu. W wyniku wykonywanej pracy energia ciała drgającego maleje, zmniejsza się też amplituda drgań. Drgania nie podtrzymywane siłą zewnętrzną ulegają tłumieniu, gasną, zanikają - stąd ich nazwy - drgania tłumione, gasnące, zanikające.

Zanikanie drgań harmonicznych może nastąpić pod wpływem działania siły hamującej F proporcjonalnej do prędkości i skierowanej do niej przeciwnie :

gdzie b jest współczynnikiem oporu.

Biorąc pod uwagę tę siłę, drgania można wyrazić :

dzieląc całe równanie przez otrzymujemy:

Korzystając z zależności : i powyższe równanie przyjmuje postać:

gdzie:

-częstość własna drgań nie tłumionych,

β -stała zaniku (współczynnik tłumienia).

Ostatecznie wychylenie wyraża się wzorem:

gdzie:

-początkowa maksymalna amplituda

- częstość drgań tłumionych.

c) drgania wymuszone.

Drgania wymuszone występują wtedy, gdy na ciało działa zewnętrzna siła okresowa.
Na przykład most drga pod wpływem maszerującej po nim kolumny żołnierzy.

Drgania wymuszone mają częstość taką, z jaką działa siła zewnętrzna. Jednak reakcja ciała zależy od stosunku, jaki zachodzi pomiędzy częstością wymuszoną a częstością własną. Równanie ruchu dla oscylatora o wymuszonej częstości drgań wynika z drugiej zasady dynamiki. Prócz siły -kx (sprowadzającej ciało drgające do położenia równowagi) i siły tłumienia -bdx/dt występuje jeszcze okresowa siła zewnętrzna. Niech siła zewnętrzna wyraża się wzorem :

gdzie F_m to wartość maksymalna siły zewnętrznej, a ω'' - jej częstością kołową. Niech siła ta jest przyłożona bezpośrednio do ciała o masie m. Z równania F=ma otrzymujemy :

rozwiązaniem tego równania jest :

gdzie:

.

Dla rzeczywistych oscylatorów tłumionych przy pewnej charakterystycznej wartości częstości wymuszającej ω'', amplituda oscylacji osiąga maksimum. Takie zjawisko nazywa się rezonansem. Zjawisko rezonansu jest zjawiskiem bardzo istotnym dla wielu urządzeń elektrycznych, akustycznych i atomowych.

2. Wahadła jako przykład ruchu harmonicznego.

1. wahadło matematyczne.

Wychylając nić o niewielki kąt od położenia pionowego i puszczając swobodnie kulkę K wywołujemy jej drgania dokoła jej położenia równowagi D . Aczkolwiek w praktyce amplituda tych drgań wskutek pokonywania oporów maleje - okres wahań należy uważać za stały. Tę własność ruchu wahadła nazywamy izochronizmem. Siły oporu pomijamy, bierzemy pod uwagę tylko siłę ciężkości KA=mg. Siłę tę rozkładamy na dwie składowe KB i KC. Składowa KC wywołuje ruch wahadła z przyspieszeniem a, a zatem jest ona równa ma. Ostatecznie siła ta wynosi:

.

Jeżeli kąt jest mały, to sin jest bardzo bliskie . Przemieszczenie wzdłuż łuku wynosi:

.

Przyjmując, że:

,

otrzymujemy:

Stała określa stałą k w równaniu . Tak więc przy małej amplitudzie okres wahadła matematycznego wynosi:

Wahadło matematyczne jest to punkt materialny zawieszony na nieważkiej i nierozciągliwej nici

gdzie l - długość wahadła, a g - przyspieszenie ziemskie.

Powyższy wzór ten można zapisać także jako :

b) wahadło fizyczne.

Wahadłem fizycznym nazywamy bryłę sztywną dowolnego kształtu, zawieszoną tak,
że może się wahać dookoła pewnej osi przechodzącej przez bryłę. Ruch wahadła fizycznego może być wywołany działaniem różnych sił. Szczególnym przypadkiem wahadła fizycznego jest wahadło fizyczne - grawitacyjne. Jest to bryła sztywna dowolnego kształtu o środku ciężkości w punkcie S, zawieszona w ten sposób, że może się obra­cać bez tarcia dookoła osi poziomej, przechodzącej przez ten punkt O. Miarą wychylenia jest kąt h. W tym położeniu na wahadło działa moment siły ciężkości równy mgdsinh skierowujący wahadło w stronę położenia równowagi. Iloczyn mgd jest maksymalną wartością momentu siły ciężkości - nazywamy go momentem kierującym wahadła grawitacyjnego. i oznaczamy literą D. Moment bezwładności bryły oznaczmy przez I. Stąd okres wahadła grawitacyjnego wynosi :

Wzór ten jest słuszny dla dowolnego wahadła fizycznego. Z wahadłem fizycznym często kojarzy się pojęcie długości zredukowanej wahadła fizycznego jest to długość wahadła matematycznego mającego ten sam okres wahań, a więc spełniającego warunek T_fiz=T_mat .

Czyli długość zredukowana wynosi:

gdzie d to odległość od osi obrotu do środka ciężkości wahadła fizycznego. Punkt odległy od osi obrotu o l_zred nazywamy środkiem wahań wahadła fizycznego. Położenie tego środka zależy od wyboru osi obrotu dla danego ciała.

3. Wykorzystanie właściwości środka wahań w konstrukcji wahadła rewersyjnego.

Wahadło rewersyjne jest to ciało sztywne, mające takie dwie osie obrotu I i II, że okresy wahań względem nich są jednakowe. Najczęściej spotykaną formą wahadła rewersyjnego jest sztaba stalowa, na której znajdują się trzy metalowe ciężary w kształcie soczewek. Dwie z nich A i B są nieruchome, trzecią C możemy przesuwać wzdłuż sztaby. Przez przesuwanie tej soczewki zmieniamy położenie środka masy wahadła, a przez to i okres wahadła. Osie obrotu I i II mają postać nieruchomo umocowanych pryzmatów i znajdują się w stałej od siebie odległości.

Wahadło rewersyjne jest to specjalnie skonstruowane wahadło fizyczne, które pozwala na bardzo dokładny pomiar l₀(długości zredukowanej).

Można udowodnić, że jeżeli w wahadle fizycznym środek wahań A uczynimy osią obrotu, to punkt O, czyli poprzednia oś obrotu, stanie się obecnie środkiem wahań, to znaczy okresy w obu przypadkach będą jednakowe.

Na podstawie twierdzenia Steinera moment bezwładności B₀ względem osi O określa wyrażenie:

gdzie B_c- moment bezwładności względem osi przechodzącej przez środek masy.

Okres wahań T₀ względem osi O można zapisać w postaci:

.

Okres wahań T_A względem osi A można zapisać w postaci:

.

Przypuśćmy, iż nie wiemy, że punkt A jest środkiem wahań wahadła fizycznego, natomiast znana nam jest na podstawie przeprowadzonych pomiarów równość okresów: T₀=T_A. Przyrównując dwa ostatnie równania otrzymujemy:

Podstawiając otrzymaną wartość okazuje się, że:

gdzie: l₀=a+b (l₀-długość zredukowana).

Uzasadniona została powyższa właściwość punktów O i A wahadła fizycznego, na której opiera się budowa wahadła rewersyjnego.

4. Przyspieszenie ziemskie i jego zależność od odległości od środka Ziemi i współrzędnych geograficznych.

Przyspieszenie ziemskie oznaczamy symbolicznie literą g. Jest ono nadawane ciałom poprzez siłę zwaną ciężarem. Ciężar jest to z kolei wypadkowa dwóch sił: siły przyciągania ziemskiego oraz siły odśrodkowej wywoływanej obrotem Ziemi. Ciężar wyrażamy wzorem: P=mg , gdzie P - ciężar, m - masa ciała, a g - to właśnie przyspieszenie ziemskie. Ciężar ciała, więc i przyspieszenie g zależy od położenia geograficznego oraz od wysokości, ponieważ :

a) wskutek spłaszczenia Ziemi na biegunach siła przyciągania jest tam większa niż na równiku.

b) siła przyciągania maleje ze wzrostem odległości od środka Ziemi, czyli wraz ze wzrostem wysokości.

c) siła odśrodkowa zależy od odległości od osi obrotu, a więc od szerokości geograficznej i wysokości nad powierzchnią Ziemi.

d) nagromadzenie większych mas (np. masywy górskie, pokładu rud) zmieniają lokalne pole grawitacyjne.

Pewne niewielkie zmiany powodowane są także przez Księżyc i Słońce.

II.OBLICZENIA WIELKOŚCI FIZYCZNYCH WYZNACZANYCH W ĆWICZENIU

L.p.	Położenie soczewki A[cm]	Zawieszenie A		Zawieszenie B		Długość zredukowana l [m.]	Przysp. Ziemskie g [m/s^2 ]
				Czas ta [s]	Okres Ta [s]			Czas tb [s]	Okres Tb [s]
1	18,4	55,03	1,834	56,43	1,881			0,844 ±0,001m	10,084 ±0,083 m/s^2
2	29,1	54,57	1,819	54,59	1,819
3	37,1	54,36	1,812	53,95	1,798
4	46,8	54,25	1,808	53,51	1,783
5	57,3	54,21	1,807	53,54	1,784
6	67,5	54,33	1,811	53,91	1,797
7	77,2	54,57	1,819	54,48	1,816
8	87,1	54,86	1,828	55,36	1,845

Okres T_a jest to 1/30 część czasu t_a podobnie uczyniłem z T_b

a) odczytanie wartości z wykresu

Dla otrzymanych wyników w przypadku zawieszenia A oraz dla zawieszenia B otrzymuję dwa wykresy.

Wartość okresu wahań średnia dla dwóch przecięć odczytana z wykresu :

T=1,82 [s]

2. obliczenia przyspieszenia ziemskiego

Długość zredukowaną obliczyłem przy użyciu katatometru mierząc dolną i górną wartość

l_o - długość zredukowana

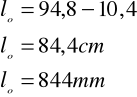
1m.=100cm=1000mm

1mm=0.1cm=0.001m

Podstawiając do wzoru na przyspieszenie ziemskie otrzymuję:

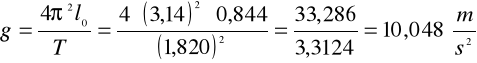
3. obliczanie błędu pomiaru

Błąd pomiaru `g' obliczam przy wykorzystaniu metody pochodnej logarytmicznej

Δl= 1mm

30*ΔT= ± 0,2s

ΔT=0,2s/30=0,00(6)s

błąd względny mierzonych wielkości :

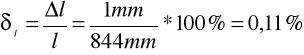
-długości

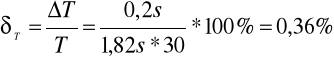
-okresu

błąd względny wyniku :

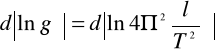
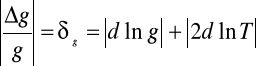
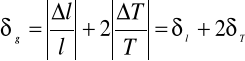
δ_g=δ_l+2δ_T=0,11%+2*0,36%

δ_g=0,83%

Δg=δ_g*g=0,83%*10,048=0.083m/s²

ostateczny wynik przyspieszenia ziemskiego wynosi :

g=(10,048
0,083)[m/s²]

III WNIOSKI

Po przeprowadzeniu ćwiczenia można stwierdzić iż otrzymany wynik przyspieszenia ziemskiego nie odbiega znacząco od wartości jaka jest powszechnie znana i obowiązująca tj. 9,81m/s². Różnice mogą wynikać min od położenia geograficznego ,wysokości nad poziomem morza itp. A także w wyniku powstałych błędów. Błędy zaliczają się do statystycznych ponieważ :

1. obliczona wartość okresu obarczona jest niedokładnością ΔT=±0,2/30s wynikająca z nieznajomości pracy urządzenia pomiarowego , czyli momentu rozpoczęcia naliczania czasu i jego zakończenia

2. wartość długości zredukowanej l₀ obarczona jest odchyłką Δl=±1mm wynikająca z niedokładności przyrządów pomiarowych

3. na błąd miały wpływ również czynniki zewnętrzne :

-temperatura

-brak doświadczenia w wykonywaniu ćwiczenia

4. odczytane wyniki naniesione na wykres nie przecięły się w tym samym punkcie co jest wynikiem powyższych czynników.

---