Sztuczna inteligencja i systemy ekspertowe
Ćwiczenie 1
Zadanie 1. Załóżmy, że ![]()
jest zbiorem liczb naturalnych. Zapisać zbiór rozmyty liczb, ![]()
, „bliskich liczby 4”.
Zadanie 2. Załóżmy, że ![]()
jest zbiorem liczb rzeczywistych. Zapisać zbiór rozmyty liczb rzeczywistych ,,bliskich liczby 4".
Zadanie 3. Za pomocą zbiorów rozmytych opisać nieprecyzyjne stwierdzenie „wyrzucenie małej liczby oczek".
Zadanie 4. Przedstawić graficznie wykresy funkcji przynależności:
4.1. singleton:
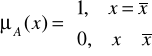
4.2. Gaussowską:
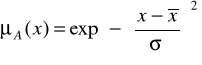
4.3. typu dzwonowego:
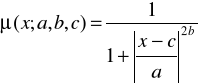
4.4. klasy s:
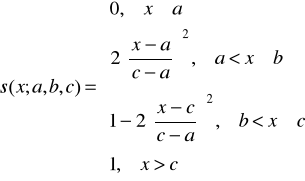
gdzie ![]()
.
4.5. klasy ![]()
:
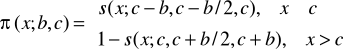
4.6. klasy ![]()
:
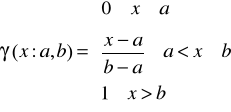
4.7. klasy t:
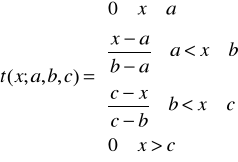
4.8 klasy L:
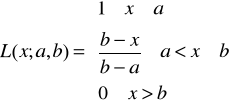
Zadanie 5. Przedstawić funkcje przynależności zbiorów rozmytych dla nieprecyzyjnych stwierdzeń:
„mała szybkość samochodu”,
„średnia szybkość samochodu”,
„duża szybkość samochódu”.
Zadanie 6. X = {1,2,3,4,5} oraz zbiór rozmyty ![]()
. Znaleźć nośnik A i wysokość A .
Zadanie 7. Znormalizować zbiór rozmyty
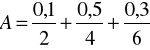
Zadanie 8. Rozważmy zbiór rozmyty ![]()
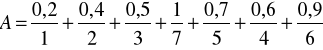
, przy czym ![]()
. Należy znaleźć poszczgólne ![]()
-przekroje oraz dokonać dekompozycji zbioru rozmytego ![]()
.
Zadanie 9. Niech ![]()
oraz
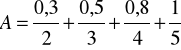
,
Wyznaczyć koncentrację i rozcieńczenie zbioru rozmytego ![]()
.
Zadanie 10. Niech ![]()
oraz
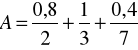
,
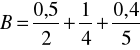
Wyznaczyć przecięcie, sumę i iloczyn zbiorów rozmytych ![]()
i ![]()
.
Zadanie 11. Niech ![]()
oraz
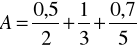
,
Wyznaczyć dopełnienie ![]()
zbioru rozmytego ![]()
, oraz ![]()
i ![]()
. Zinterpretować wyniki, porównując z odpowiednimi operacjami w logice klasycznej.
Zadanie 12. Niech ![]()
, ![]()
oraz
![]()
,
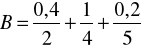
Wyznaczyć iloczyn kartezjański zbiorów rozmytych ![]()
i ![]()
.
Zadanie 13. Niech ![]()
i ![]()
. Rozważmy relację rozmytą ![]()
, określoną na iloczynie kartezjańskim ![]()
, reprezentowaną przez macierz
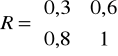
.
Znaleźć projekcję relacji ![]()
na przestrzeń ![]()
.
Zadanie 14. Niech ![]()
, ![]()
i ![]()
. Rozważmy rozmyte relacje
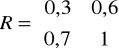
oraz
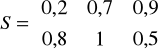
określone na iloczynach kartezjańskich ![]()
oraz ![]()
. Wyznaczyć złożenie typu max-min relacji ![]()
i ![]()
.
Zadanie 15. Niech ![]()
i ![]()
. Zbiór rozmyty ![]()
jest postaci
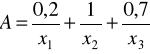
,
natomiast relację ![]()
reprezentuje macierz
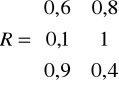
,
gdzie ![]()
i ![]()
. Wyznaczyć złożenie typu max-min macierzy ![]()
i relacji ![]()
.
Zadanie 16. Niech
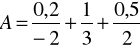
.
Wyznaczyć zbiór rozmyty ![]()
indukowany przez odwzorowanie ![]()
.
Zadanie 17. Załóżmy, że ![]()
jest iloczynem kartezjańskim zbiorów ![]()
. Zdefiniujemy następujący zbiór rozmyty ![]()
liczb „bliskich liczbie 3”
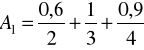
oraz zbiór rozmyty ![]()
liczb „bliskich liczbie 4”
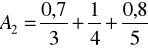
.
Wyznaczyć zbiór rozmyty ![]()
indukowany przez odwzorowanie
![]()
.
Podać interpretację zbioru rozmytego ![]()
.
Zadanie 18. Dodać oraz pomnożyć dwie liczby rozmyte postaci
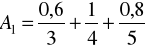
,
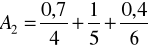
.
4
Wyszukiwarka