Dr Aleksander Klosow
PWSZ Legnica
Algorytmy i Struktury Danych
Wykład
TEORIA GRAFÓW. ALGORYTMY GRAFOWE.
[1] www.binboy.org
[2] www.algorytm.cad.pl
[3] P.Wróblewski, Algorytmy, struktury danych i techniki programowania
ALGORYTMY GRAFOWE
KLASYFIKACJA WSTĘPNA
OPERACJE NA GRAFACH
Suma grafów
Kompozycja grafów
Potęga grafów
Transpozycja grafu
POSZUKIWANIE WIERZCHOŁKA
Przeszukiwanie wszerz
Przeszukiwanie w głąb
POSZUKIWANIE DROGI
Najkrótsze ścieżki z jednym źródłem
Najkrótsze ścieżki z całym grafem
INNE
Sortowanie topologiczne
Sieci przepływowe
PRZESZUKIWANIE GRAFÓW
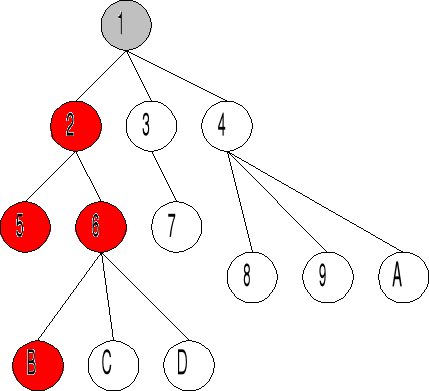
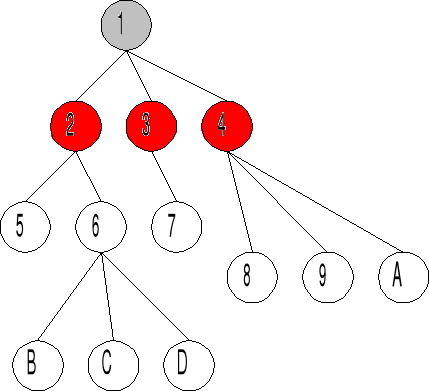
Przeszukiwanie w głąb (DFS) Przeszukiwanie w wszerz (BFS)
|
|
Istnieją dwie taktyki 'chodzenia' po grafie BFS oraz DFS. Algorytmy te mogą być częścią innych algorytmów, n.p. poszukiwanie ścieżek, poszukiwanie wierzchołków, budowanie drzew rozpinających.
PRZESZUKIWANIE GRAFÓW
Przeszukiwanie w wszerz (BFS)
funkcja BreadthFirstSearch (Graf G, Wierzchołek s)
dla każdego wierzchołka u z G:
kolor[u] = biały
odleglosc[u] = inf
rodzic[u] = NIL
kolor[s] = SZARY
odleglosc[s] = 0
rodzic[s] = NIL
Q.push(s)
dopóki kolejka Q nie jest pusta:
u = Q.pop()
dla każdego v z listy sąsiedztwa u:
jeżeli v jest biały:
kolor[v] = SZARY
odleglosc[v] = odleglosc[u] + 1
rodzic[v] = u
Q.push(v)
kolor[u] = CZARNY
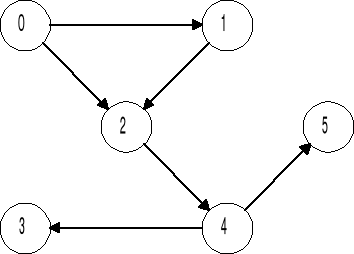
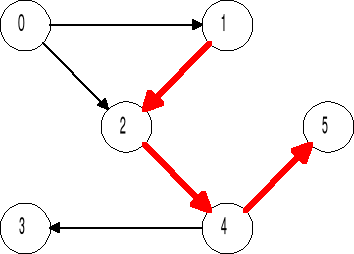
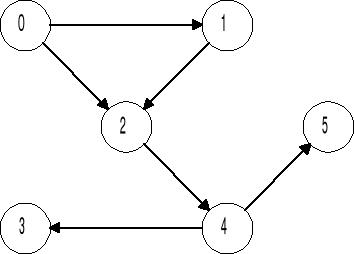
ZNALEZIENIE DROGI W GRAFIE
Dano graf: macierz sąsiedztwa - zmodyfikowana
Zadanie: znaleźć drogę od wierzchołka A do wierzchołka B
|
0 1 2 3 4 5
0
1 2
1
2
2
4
3
4
3
5
5
|
Rozwiązanie:
Przekształcić macierz (wykorzystując domknięcie grafu wg algorytmu Roy-Warszalla)
Wypisać drogę przechodząc po grafie.
ZNALEZIENIE DROGI W GRAFIE, c.d.
Etap 1. Przekształcenie macierzy wejściowej
void Mod(int g[N][N]) { int x,y,z; for(x=0;x<N;x++) for(y=0;y<N;y++) if(g[y][x]) for(z=0;z<N;z++) if(g[y][z]==0 && g[x][z]!=0) g[y][z] = g[y][x]; }
|
0 1 2 3 4 5
0
1 2 2 2 2
1
2 2 2 2
2
4 4 4
3
4
3
5
5
|
ZNALEZIENIE DROGI W GRAFIE, c.d.
Etap 2. Wypisanie drogi:
void Droga(int _od, int _do, int g[N][N])
{
int k;
int x=_od, y = _do;
if(g[x][y]==0) printf("\nDroga od %d do %d: Drogi nie ma!",x,y);
else {
printf("\nDroga od %d do %d: %d ",_od,_do,_od);
k=x;
while(k!=y)
{
k = g[k][y];
printf("%d ",k);
}
}
}
ZNALEZIENIE DROGI W GRAFIE, c.d.
Program główny::
void main() { // jezeli istnieje krawedz (x-y) to r[x][y] = y int r[N][N]={ {0,1,2,0,0,0}, {0,0,2,0,0,0}, {0,0,0,0,4,0}, {0,0,0,0,0,0}, {0,0,0,3,0,5}, {0,0,0,0,0,0} }; int _od = 1, _do = 5; clrscr(); Mod(r); Droga(_od,_do,r); getch(); }
|
|
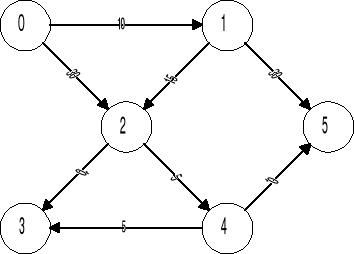
ALGORYTM ROY-WARSZALLA
Algorytm Roy-Warszalla służy do wyznaczenia domknięcia przechodniego grafu.
Graf nazywamy przechodnim jeżeli każda droga o długości większej lub
równej 1 jest podtrzymywana przez jakąś krawędź.
Domknięcie grafu pozwala odpowiedzieć na pytanie:
"czy możliwe jest przejście po krawędziach grafu od jednego wierzchołka do drugiego".
|
Macierz sąsiedztwa |
Macierz z domknięciem |
Macierz z domknięciem pozwala wyciągnąć pewne wnioski:
z wierzchołka 0 da się przejść do dowolnego innego wierzchołka,
natomiast, z 3 oraz 5 nie da się przejść nigdzie.
ALGORYTM ROY-WARSZALLA
Realizacja w języku C
void Roy(int g[N][N]) { int x,y,z; for(x=0;x<N;x++) for(y=0;y<N;y++) for(z=0;z<N;z++) if(g[y][z]==0) g[y][z] = g[y][x]*g[x][z]; }
|
void main() { int r[N][N]={ {0,1,1,0,0,0}, {0,0,1,0,0,0}, {0,0,0,0,1,0}, {0,0,0,0,0,0}, {0,0,0,1,0,1}, {0,0,0,0,0,0} }; clrscr(); // -------------- Pokaz(r); Roy(r); Pokaz(r); // -------------- getch(); } |
POSZUKIWANIE NAJKRÓTSZYCH ŚCIEŻEK
ALGORYTM FLOYDA
Algorytm Floyda służy do obliczenia najkrótszej drogi w grafie między wierzchołkami.
Nie daje odpowiedzi jaka to jest droga.
|
0 1 2 3 4 5
0 0 10 30
1
0 15
30
2
0 10 5
3
0
4
5 0 10
5
0
Macierz sąsiedztwa |
0 1 2 3 4 5
0 0 10 25 35 30 40
1
0 15 25 20 30
2
0 10 5 15
3
0
4
5 0 10
5
0
Wynik A. Floyda |
ALGORYTM FLOYDA
Realizacja w języku C
// Algorytm Floyda #include <stdio.h> #include <conio.h>
#define N 6 #define INF 1000 #define min(a,b) (a<=b?a:b)
void Floyd(int g[N][N]) { int x,y,z; for(x=0;x<N;x++) for(y=0;y<N;y++) for(z=0;z<N;z++) g[y][z] = min(g[y][z],g[y][x]+g[x][z]); } |
void main() { int r[N][N]={ {0,10,30,INF,INF,INF}, {INF,0,15,INF,INF,30}, {INF,INF,0,10,5,INF}, {INF,INF,INF,0,INF,INF}, {INF,INF,INF,5,0,10}, {INF,INF,INF,INF,INF,0} }; clrscr(); // -------------- Pokaz(r); Floyd(r); Pokaz(r); // -------------- getch(); } |
1
4
2
3
5
6
0
Q
0
1
1
4
2
3
5
6
1
1
0
Q
1
2
5
1
Q
1
4
2
3
5
6
2
0
1
1
2
2
6
2
Wyszukiwarka