Część II
PRZEPISZ STARANNIE - ZWRACA NA TO UWAGE, PRZEPISZ TAK ŻEBY PRACA NIE BYŁA PODOBNA - INNI MOGĄ MIEC TAKIE SAME I CO WTEDY?
Zadanie 1 - wyprowadzić równania dynamiki płynu lepkiego (r-nia Naviera-Stokesa)

-czasoprzestrzeń wypełniona płynem
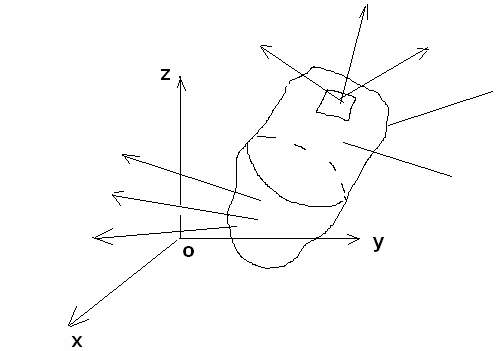
Rozpatrzmy dowolny obszar Ω:
![]()
![]()
![]()
![]()
V(t,x) - pole prędkości
fv(t,x) - pole sił objętościowych
![]()
p(t,x) - pole gęstości pędu
![]()
JTn - wektor prądu konwekcyjnego
![]()
![]()
σTn - wektor naprężeń
![]()
![]()
Prawo Newtona mówi o tym, że: ![]()
dla każdego obszaru Ω. Pochodna pędu (zmiana pędu) jest równa sumie sił działających na ten obszar.
![]()
Korzystając z Tw. Gaussa Ostrogradskij-ego doprowadzamy równanie do postaci:
![]()
Dla płynu lepkiego mamy zależności:
![]()
, ![]()
i po podstawieniu: ![]()
σL - tensor naprężeń związanych z odkształceniem postaciowym - zw. z lepkością
![]()
- tensor prędkości odkształcenia postaciowego. (dewiator prędkości odkształcenia postaciowego)
μ - lepkość dynamiczna płynu
![]()
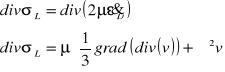
- gdzie ![]()
- operator Laplace'a
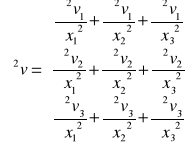
Ponieważ: ![]()
to dalej możemy napisać:
![]()
Podążając dalej mamy zależnośc na siłę wypadkową:

Z bilansu pędu wiemy, że:
![]()
gdzie p - cisnienie! P - pęd! - to pisz jako takie smieszne IP - jak na wykladzie oznaczal - tak było wiec niech tak zostanie..
Korzystając z Tw. Gaussa-Ostrogradskij-ego:
![]()
i podstawiając:
![]()
Wiedząc, że ![]()
, oraz ![]()
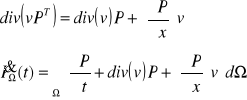
a wiemy, że: ![]()
to pochodna materialna ![]()
![]()
podstawiając ![]()
mamy:
![]()
oraz podstawiając dalej:

Prawo zachowania masy prowadzi do zależności: ![]()
, a zatem:
![]()
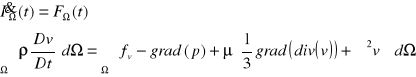
Porównując wyrażenia podcałkowe, otrzymujemy równanie dynamiki płynu lepkiego:
![]()
![]()
![]()
- funkcja ciśnienia
Są to równania dynamiki płynu lepkiego, zwane równaniami Naviera-Stokes
Zadanie 2 - gaźnik
d= |
? |
[mm] |
|
λ= |
0,7 |
[-] |
D= |
23 |
[mm] |
|
ρp= |
1,3 |
[kg/m3] |
h= |
2 |
[mm] |
|
ρb= |
700 |
[kg/m3] |
Ne= |
23 |
[kW] |
|
g= |
9,81 |
[m/s2] |
ge= |
200 |
[g/kWh] |
|
|
|
|
λ =Qp/(14,7 Qb)
Qp, Qb - wydatki masowe
powietrza i benzyny
Obliczam wydatek masowy benzyny i powietrza:
Qb = ge*N = 200 g/kWh * 23 kW = 4600 g/h = 1,28 * 10-3 kg/s
Qp = 14,7 * λ * Qb = 14,7*0,7 * 1,28 * 10-3 = 0,0131 kg/s
Obliczam wydatki objętościowe: Qv = Q / ρ
Qvp = Qp / ρp = 0,0131/ 1,3 = 0,0101 m3/s
Qvb = Qb / ρb = 1,28 * 10-3 / 700 = 1,82 * 10-6 m3 / s
Wiemy, że ![]()
wtedy:
Vp = Qvp * 4 / (πD2) = 0,0101 *4 / (π * 0,0232) = 24,3 m/s
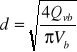
; Vb = ? - obliczamy z równań Bernoulliego, wiedząc, że pp1 = pb1
Równanie dla powietrza w przekrojach 1-2:
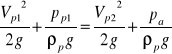
przy czym zakładamy :
Brak różnicy wysokości pomiędzy przekrojami,
Vp2 = 0 bo średnica wlotu jest duża,
![]()
pp1 = 101325 - 1,3*24, 32 /2= 100939 [Pa]
pp1 = pb1 - wiedząc to, obliczamy Vb z równania Bernoulliego dla benzyny dla przekrojów 0 - 1
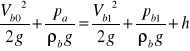
Przy czym zakładamy ze Vb0 = 0 ze względu na dużą powierzchnię komory pływakowej. Podstawiam pp1 = pb1 i obliczam prędkość benzyny:

Vb1 = pierwiastek ( 2*9,81*((101325 - 100939)/700 - 0,002)) = 3,3 m/s
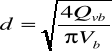
Po podstawieniu obliczamy średnice dyszy:
d = pierwiastek (4 * 1,82 * 10-6/ (π *3,3)) = 0,000841m = 0,85 mm
Zadanie 3 - turbina Peltona
N= |
160 |
kW |
H= |
80 |
m |
r= |
0,54 |
|
α= |
0,47 |
|
β= |
19 |
|
g= |
9,81 |
m/s |
ρwody= |
1000 |
kg/m3 |
Ze wzoru Toricellego obliczam prędkość wody spadającej z danej wysokości:
![]()
= 40 m/s
Obliczam prędkość łopatki:
![]()
czyli u = α * V 0 = 0,47* 40 = 18,6 m/s
Wiedząc, że ![]()
możemy napisać, ze ![]()
F = 160 kW / 18,6m/s = 8,6 kN - jest odpowiedź na pytanie o wymagana siłę naporu wody na łopatki turbiny
Dalej obliczamy wydatek masowy wody wymagany do uzyskania takiej siły, przy czym:
Vo - to prędkość strugi wody wypływającej z dyszy
W - prędkość tej samej strugi wody względem łopatki poruszającej się z prędkością u
U - prędkość obwodowa łopatki turbiny
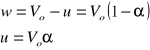
Siła naporu wody na łopatkę jest równa zmianie pędu wody.
Początkowo woda wypływa z dyszy z prędkością Vo (względem ziemi), a po uderzeniu i odbiciu od łopatki porusza się w przeciwnym kierunku do ruchu łopatki, pod kątem beta. Prędkość w jest prędkością względem łopatki, i żeby móc obliczyć pęd końcowy strugi, należy obliczyć składowa prędkości, równoległa do Vo, wody odbitej względem nieruchomego układu - np. związanego z dysza wypływowa/ziemia. Niech to będzie w1. Zakładamy w1 skierowane w lewa stronę - czyli przeciwnie do Vo.
![]()
w1= |
3,39 |
[m/s] |
Siła naporu wody na łopatkę to różnica pędów początkowego i końcowego cieczy, ponieważ w1 jest skierowane przeciwnie, pęd końcowy ma znak ujemny:
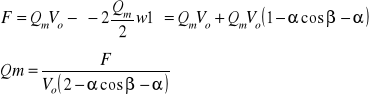
Qm= |
199,8 |
[kg/s] |
Wydatek objętościowy:
Qv = Qm / ρwody = 0,2 m3 / s
![]()
oraz z tego, że: 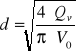
obliczam średnicę dyszy:
d = 0,080 m = 80 mm - jest to odpowiedź na drugie z pytań.
Zadanie 4 - Rurociąg
![]()
Rysunek rozpatrywanego rurociągu
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Dane instalacji:
ζf= |
4 |
[-] |
Ql= |
57 |
[l / s] |
ζk= |
0,275 |
[-] |
d= |
260 |
[mm] |
ζz= |
0,8 |
[-] |
h1= |
1,7 |
[m] |
ρwody= |
1000 |
[kg/m3] |
h2= |
5,5 |
[m] |
ν= |
1,00E-06 |
[m2/s] |
h3= |
24 |
[m] |
pa= |
101325 |
[Pa] |
l1= |
33,5 |
[m] |
g= |
9,81 |
[m/s2] |
l2= |
120 |
[m] |
|
|
|
l3= |
340 |
[m] |
Ponadto istnieja zaleznosci: |
|
|
|
||
ζt=2ζk= |
0,55 |
[-] |
l4=5l2= |
600 |
[m] |
h4=h3= |
24 |
[m] |
l5=l3= |
340 |
[m] |
Pierwszą rzeczą jaką sprawdzam, jest prędkość przepływu wody przez pompę:
Wiedząc, że:
![]()
obliczam prędkość przepływu strugi wody:
![]()
= 4*0,057 [m3/s] /(π * 0,260 2) = 1,07[m/s]
Jest to jednak tylko prędkość w początkowym, nierozgałęzionym odcinku rurociągu.
Należy zatem obliczyć jakie prędkości będą miały strugi wody w poszczególnych gałęziach za trójnikiem.
![]()
czyli ![]()
gdzie Va i Vb to prędkości strugi w gałęziach rurociągu, a A, Aa i Ab to przekroje rury. Ze względu na stałą średnice rury - pole przekroju rury jest takie samo i możemy je skrócić, wtedy ostateczną zależnością pomiędzy prędkościami Va i Vb jest: ![]()
Następnie należy obliczyć jaka część strugi popłynie gałęzią A - do pierwszego(bliższego) zbiornika a jaka gałęzią B - do dalszego zbiornika.
Zauważając że ciśnienie tuż za trójnikiem w obu gałęziach będzie takie samo, a ciśnienie wylotu jest równe ciśnieniu atmosferycznemu, można napisać równania Bernoulliego:
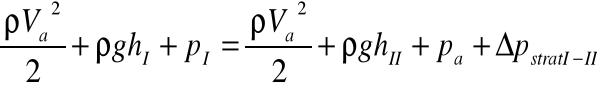
Dla gałęzi A:
![]()
![]()
- jest to poziom odniesienia; ![]()
- wysokość nad poziomem odniesienia; i wtedy:
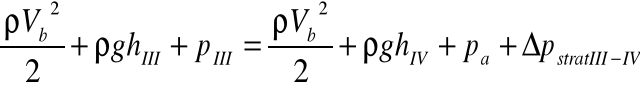
Dla gałęzi B:
![]()
![]()
- jest to poziom odniesienia; ![]()
- wysokość nad poziomem odniesienia; i wtedy:
Porównując ciśnienia w przekroju I i III - (sa one równe) otrzymujemy:
![]()
Ponieważ h3 = h4 to:
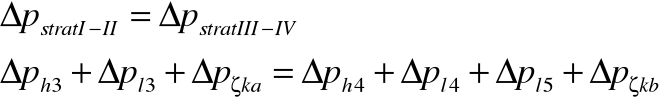
Przy czym straty zarówno lokalne jak i liniowe zależą od prędkości przepływu strugi przez dany element, a tych prędkości nie znamy.
Podstawiając zależności na straty lokalne i liniowe:
![]()
-straty liniowe ![]()
-straty lokalne
Mamy:
![]()
Skracajc przez gęstość wody i przekształcając:
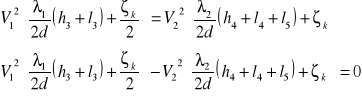
Równanie w takiej postaci należy rozwiązać .
Oba odcinki będą charakteryzować sie rożnymi prędkościami, czyli również innymi liczbami Reynoldsa, co przekłada się na rożne współczynniki lambda.
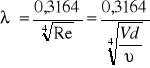
gdzie ![]()
Ze względu na to że rozwiązanie wymaga skomplikowanego aparatu matematycznego, można rozwiązać je iteracyjnie w arkuszu kalkulacyjnym Excel, podstawiając kolejno wartości Va i Vb od zera, takie aby w sumie dawały obliczona prędkość strugi.
V= |
1,07 |
[m/s] |
![]()
Dla każdych wartości Va i Vb obliczyć należy odpowiednia lambdę. Ponieważ lambda jest rożna dla przepływu laminarnego i burzliwego, zakładam najpierw, ze przepływ będzie w obu strugach burzliwy i sprawdzę czy to założenie jest prawdziwe dla znalezionych prędkości (czyli sprawdzę czy liczby Reynoldsa dla obu gałęzi są większe od 2340). Zbudowany arkusz i fragment będący rozwiązaniem:
(tego nie pisz raczej, ale jakoś żeby pokazać jak ten arkusz wygląda, jak to policzyłeś)
Va |
Vb |
λa |
λb |
Równ. |
Re a |
Re b |
0,69 |
0,38 |
0,0154 |
0,0178 |
-0,419 |
180333 |
98800 |
0,68 |
0,39 |
0,0154 |
0,0177 |
-0,063 |
177733 |
101400 |
0,67 |
0,4 |
0,0155 |
0,0176 |
0,2954 |
175133 |
104000 |
0,66 |
0,41 |
0,0155 |
0,0175 |
0,6571 |
172533 |
106600 |
Dla obu galezi przy rozwiązaniu Va i Vb obie liczby Reynoldsa są większe od 2340, założenie jest prawdziwe.
Obliczam liczbę Reynoldsa dla odcinka A:
Ostatecznie przyjmuję rozwiązanie jako:
Va= |
0,68 |
[m/s] |
λa= |
0,0154 |
Vb= |
0,39 |
[m/s] |
λb= |
0,0177 |
Następnie mogę napisać równanie Bernoullego dla przekroju 1- (I i III) - ponieważ ciśnienie tuz za trójnikiem jest już obliczone na początku zadania, wystarczy porównać tylko te przekroje. Dzięki temu będzie można obliczyć wymagany przyrost ciśnienia jaki musi dać pompa:
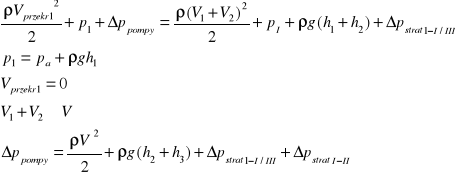
![]()
- straty na tym odcinku liczone są dla prędkości strugi takiej jaka jest w tej gałęzi.
![]()
Vprzekr1=0 (to co jest powyżej) - ponieważ powierzchnia wlotowa filtra jest duża w porównaniu z powierzchnią przekroju rury
Straty ciśnienia obliczam tak jak powyżej, wiedząc że oba przepływy są burzliwe (Re większa od krytycznej).
![]()
; ![]()
; ![]()
;
Δpf= |
2305 |
Pa |
Δpt= |
317 |
Pa |
Δpz= |
461 |
Pa |
Δph1= |
58 |
Pa |
Δpl1= |
1144 |
Pa |
Δph2= |
188 |
Pa |
Δpl2= |
4096 |
Pa |
Δpk= |
158 |
Pa |
dla odcinka A (do części równania w której obliczone jest pI)
Va= |
0,68 |
[m/s] |
Δph3= |
329 |
Pa |
Δpl3= |
4656 |
Pa |
ΔpK= |
64 |
Pa |
Obliczona po podstawieniu wartość przyrostu ciśnienia jakie musi dać pompa:
Δppompy= |
303747 |
Pa |
Moc pompy możemy określić z zależności:
![]()
= 303747 *0,057= 17314 [W] = 17,5 [kW]
Punktem podejrzanym o zaistnienie kawitacji jest punkt w którym wystąpi najniższe ciśnienie. Jest to punkt tuż przed pompą. W celu obliczenia minimalnego ciśnienia i sprawdzenia czy w rurociągu nie wystąpi kawitacja piszę równanie Bernouli'ego dla przekrojów 1-2:
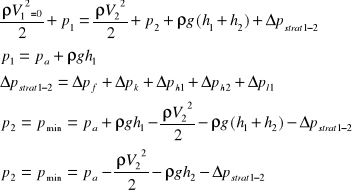
Δp1-2= |
3853 |
Pa |
pmin = 101325 - 1000*1,072 /2 - 9,81*1000*5,5-3853= 42941 [Pa]
jest to najniższe ciśnienie. Ciśnienie minimalne dopuszczalne aby nie zaistniała kawitacja to 15 [kPa], obliczona wartość minimalna w rurociągu jest większa, zatem nie ma zagrożenia powstania kawitacji.
1
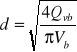
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
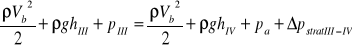
![]()
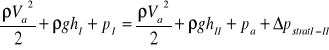
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Wyszukiwarka