POLITECHNIKA WROCŁAWSKA Laboratoria z podstaw Fizyki
Tomasz Kaczor Tomasz Goździuk	Sprawozdanie z ćwiczenia nr 29 Temat: Wyznaczanie współczynnika rozszerzalności cieplnej metodą elektryczną.
Wydział Chemiczny Rok I	Prowadzący: dr Ewa Oleszkiewicz	Ocena:

1. Wstęp teoretyczny

Celem przeprowadzonego ćwiczenia było zapoznanie się :

- ze zjawiskiem rozszerzalności cieplnej ciał stałych;

- z jedną z metod pomiaru współczynnika rozszerzalności cieplnej metali.

Zjawisko rozszerzalności cieplej polega na zmianie rozmiarów ciał spowodowanej wzrostem temperatury, jeśli w danym zakresie temperatur nie występują przejścia fazowe. Zwiększonym rozmiarom ciała odpowiada w obrazie mikroskopowym większa średnia odległość między jego atomami. Wzrost średnich odległości międzyatomowych towarzyszący wzrostowi temperatury ciała, znajduje uzasadnienie w charakterze wzajemnych oddziaływań między atomami tego ciała.

Między atomami ciał stałych, cieczy i gazów występują zarówno siły przyciągania jak i odpychania. Zależność tych sił od wzajemnej odległości między atomami jest różna. Dla bardzo małych odległości przeważają siły odpychania, dla większych - przyciągania. Gdy odległość między sąsiadującymi atomami jest mniejsza od r₀ przeważają siły odpychania, gdy odległość ta jest większa od r₀ - siły przyciągania. W ten sposób r₀ jest odległością między atomami, odpowiadającą stanowi równowagi, w jakiej znajdowałyby się atomy wówczas, gdyby nie było ruchu cieplnego zakłócającego równowagę. Ze wzrostem temperatury zwiększa się amplituda drgań poszczególnych atomów. Siła przywracająca atom do położenia równowagi nie ma przebiegu liniowego w otoczeniu punktu r₀ , czego konsekwencją jest asymetria krzywej przedstawiającej zależność energii potencjalnej od wzajemnej odległości między atomami. Atom o całkowitej energii równej E drga wokół punktu r₀, któremu odpowiada minimum energii potencjalnej, Maksymalne wychylenia atomu z położenia równowagi nie są symetryczne względem r₀ . Wraz ze wzrostem energii obszar dostępny dla danego atomu poszerza się, co odpowiada większej amplitudzie drgań, a średnie położenie atomu względem najbliższego sąsiada przesuwa się ku wartościom większym od r₀.

Zwiększenie średniej odległości między atomami ciała stałego podczas jego nagrzewania jest przyczyną liniowej i objętościowej rozszerzalności ciała. W celu ilościowego ujęcia zjawiska rozszerzalności cieplnej ciał stałych wprowadza się pojęcie współczynnika rozszerzalności liniowej α. Można go zdefiniować równaniem :

, gdzie
- średnia odległość od r₀

Badanie rozszerzalności cieplnej ciał stałych jest oparte zwykle na prawie opisującym zależność długości ciała od temperatury :

lt = l₀(1 +  T)

gdzie

lt - długość drutu w temperaturze T,

l₀ - długość drutu w temperaturze T₀,

ΔT = T - T₀,

α - współczynnik rozszerzalności liniowej.

Przekształcenie powyższego równania pozwala wyznaczyć współczynnik α na podstawie zmierzonej zależności względnego wydłużenia od przyrostu temperatury.

α =
[ 1/K ]

gdzie Δl = 1/2 Δl' = ( l_t - l₀ ), gdyż odczytane przyrosty są dwukrotnie większe od rzeczywistych Δl z powodu zastosowania przekładni mechanicznej.

Wartość współczynnika jest też równa tangensowi kąta nachylenia krzywej na wykresie, przedstawiającym zależność wydłużenia względnego od przyrostu temperatury.

Zestaw przyrządów:

- czujnik mikrometryczny do pomiaru wydłużenia drutu;

- amperomierz i woltomierz;

- zasilacz prądu stałego;

- cyfrowy miernik temperatury;

- transformator zabezpieczający.

2. Tabela pomiarowa.

l₀ = 0,890
0.004 m = 890
4 [mm]

t₀ = 24.8 ± 0.1° C

Pomiar temperatury drutu : Odczyt czujnika mikrometrycznego :

ti [ * C ]		Δli' [mm]
t­1 = 34.6		Δl1' = 0.13
t2 = 44.9		Δl2' = 0.28
t3 = 54.8		Δl3' = 0.45
t4 = 65.0		Δl4' = 0.54
t5 = 75.5		Δl5' = 0.74
t6 = 85.1		Δl6' = 0.88
t7 = 95.4		Δl7' = 1.01
t8 = 105.2		Δl8' = 1.21
t9 = 115.4		Δl9' = 1.37
t10 = 124.9		Δl10' = 1.53
t11 = 135.5		Δl11' = 1.72

Obliczając odpowiednio Δl_i = 1/2 Δl_t' - przyrosty długości drutu oraz Δt_i = t_i - t₀ , czyli

przyrosty temperatury otrzymujemy następujące wyniki :

Δti [ * C ]		Δli [mm]
Δt­1 = 9.8		Δl1 = 0.065
Δt2 = 20.1		Δl2 = 0.140
Δt3 = 30.0		Δl3 = 0.225
Δt4 = 40.2		Δl4 = 0.270
Δt5 = 50.7		Δl5 = 0.370
Δt6 = 60.3		Δl6 = 0.440
Δt7 = 70.6		Δl7 = 0.505
Δt8 = 80.4		Δl8 = 0.605
Δt9 = 90.6		Δl9 = 0.685
Δt10 = 100.1		Δl10 = 0.765
Δt11 = 110.7		Δl11 = 0.860

3. Wyznaczenie współczynnika rozszerzalności liniowej.

Wykres zależności
= f(ΔT) .

Korzystamy z powyższej tabelki ( pobieramy Δt_i ) oraz z obliczonych
.

Δli/l0 * 10^-6 [mm]

73.03	157.30	252.81	303.37	415.73	494.38	567.42
679.78	769.66	859.55	966.29

Opis wykresu :

- oś rzędnych ( OY )
*10^-6 [mm]

- oś odciętych ( OX ) - ΔT [K]

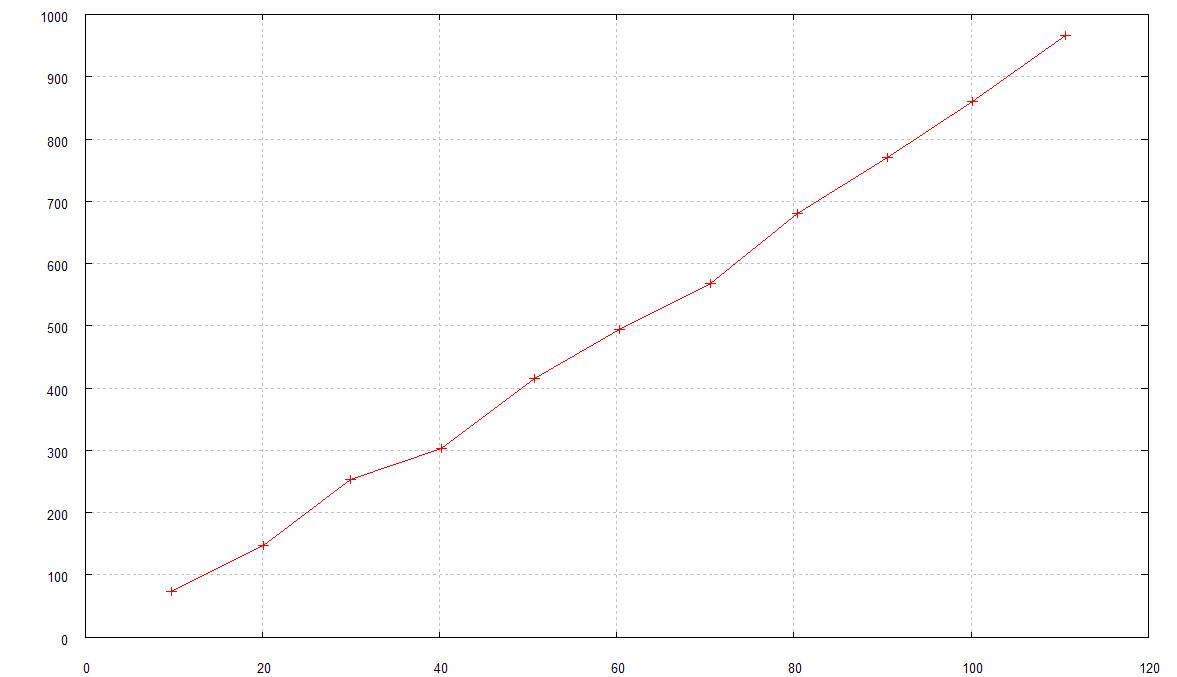
Z wykresu wynika, że kąt nachylenia krzywej wynosi około ≅ 40°

Przykładowo dla i = 5 otrzymujemy :

i = 8 i = 11

α₈ = 0.85*10^-5 α₁₁ = 0.87*10^-5

Uśredniając α_śr będzie wynosić około 0.81 [1/K]

6. Obliczanie błędu pomiaru.

Przy obliczaniu błędu należy uwzględnić niedokładność pomiaru przyrostu długości drutu.

W związku z tym należy określić błąd wynikający z określenia prawidłowości ustawienia wskazówki na tle skali lustrzanej. Trzeba też wziąć pod uwagę błąd wcześniejszego pomiaru długości drutu. W naszym przypadku wyniósł on : Δl₀ = 0.004 m = 4 mm ( dane pobrane zostały z instrukcji roboczej ).

Oto pomiar ustawienia wskazówki na tle skali lustrzenej ( odczyt wskazania czujnika mikrometrycznego w temperaturze pokojowej ):

	pomiar [mm]
	0.04
	0.035
	0.02
	0.01
	0.025
	0.04
	0.03
	0.02
	0.03
	0.031
średnia	0.0281

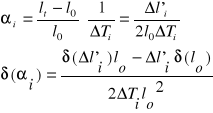
δ(Δl_i') = 0.0281 [mm]

δ(l_o) = 4.00 [mm]

Przykładowo :

Błąd bezwzględny :

7. Uwagi i wnioski.

Współczynnik rozszerzalności liniowej α wyznaczono w ćwiczeniu na podstawie wykresu zależności względnego wydłużenia drutu w funkcji temperatury. Jest on równy tangensowi kąta nachylenia krzywej. Zależność ta jest liniowa. Nieliniowość charakterystyki dla większych temperatur mogła być spowodowana niejednakową temperaturą na całej długości drutu. Otrzymana wartość współczynnika rozszerzalności liniowej porównywalna jest z wartościami tego współczynnika dla metali.

---