1. Wprowadzenie

Ilość ciepła wydzielonego (względnie pochłoniętego) w kalorymetrze przez 1 mol reagenta obliczamy ze wzoru:

(*)

gdzie:

K - pojemność cieplna układu kalorymetrycznego

∆t - zmiana temperatury układu kalorymetrycznego

Σv - poprawka uwzględniająca wymianę ciepła z otoczeniem podczas pomiaru

m - odważka substratu wziętego w nadmiarze stechiometrycznym

M - masa molowa tego substratu

Jeżeli w kalorymetrze zachodzi jednocześnie kilka procesów o różnych efektach to oznaczona wielkość jest ich sumą:

Q = q₁ + q₂ + q₃ + …itd.

Ciepło rozpuszczania - ciepło jakie wydzieliło się podczas rozpuszczania 1 mola substratu w takiej ilości rozpuszczalnika, że powstanie roztwór nasycony.

Ciepło zobojętniania - ciepło powstałe w reakcji zobojętniania kwasu z zasadą, w wyniku której powstaje woda i sól. Efekt cieplny łączenia się jonów H⁺ i OH^-.

W celu wykonania ćwiczenia (pomiar ciepła zobojętniania) posłuży nam kalorymetr diatermiczny. Jest on używany do oznaczania ciepła reakcji chemicznych w fazie ciekłej. Osłonę zewnętrzną kalorymetru stanowi naczynie Dawera (termos), które ma na celu zmniejszyć wymianę ciepła między kalorymetrem a otoczeniem.

Sposób wykonania doświadczenia: do naczynia Dowera wlewamy 600ml zwykłej wody. W uchwycie umieszczamy szklaną ampułkę ze znaną ilością kwasu siarkowego. Przykręcamy mieszadełko, które spowoduje, że temperatura cieczy wszędzie będzie taka sama. Umieszczamy sondę pomiarową w przeznaczonym na nią miejscu. Po zmontowaniu całego urządzenia wykonujemy 10 pomiarów co 30 sekund. Następnie tłuczemy ampułkę tak, aby kwas siarkowy zmieszał się z wodą. Kolejne 10 pomiarów odczytujemy co 10 sekund, a następne 10 co 30 sekund. Drugą część doświadczenia wykonujemy analogicznie tylko zamiast wody w naczyniu Dowera umieszczamy wodny roztwór wodorotlenku sodu.

H₂SO₄ + 2NaOH → 2H₂O + Na ₂SO₄

2. Pomiary i obliczenia

Masa kwasu siarkowego w 1. ampułce - 3,005 g

Masa kwasu siarkowego w 2. ampułce - 2,08 g

Objętość wodorotlenku sodu - 3,62 cm³

(1) Ampułka zanurzona w wodzie				(2) Ampułka zanurzona w roztworze NaOH
L.p..	Czas (s)	Rezystancja kΩ	Temperatura (˚C)	Czas (s)	Rezystancja kΩ	Temperatura (˚C)
1	30	22,86	15,023	30	24,40	13,617
2	60	22,86	15,023	60	24,40	13,617
3	90	22,865	15,018	90	24,40	13,617
4	120	22,865	15,018	120	24,405	13,613
5	150	22,87	15,014	150	24,405	13,613
6	180	22,87	15,014	180	24,405	13,613
7	210	22,875	15,009	210	24,405	13,613
8	240	22,875	15,009	240	24,405	13,613
9	270	22,88	15,004	270	24,405	13,613
10	300	22,88	15,004	300	24,405	13,613
Pomiary po stłuczeniu ampułki z kwasem siarkowym (H2SO4)
11	310	22,20	15,659	310	23,47	14,454
12	320	22,09	15,768	320	23,36	14,555
13	330	22,08	15,777	330	23,34	14,573
14	340	22,07	15,787	340	23,33	14,583
15	350	22,07	15,787	350	23,33	14,583
16	360	22,07	15,787	360	23,33	14,583
17	370	22,07	15,787	370	23,33	14,583
18	380	22,07	15,787	380	23,33	14,583
19	390	22,07	15,787	390	23,33	14,583
20	400	22,08	15,777	400	23,33	14,583
21	430	22,08	15,777	430	23,33	14,583
22	460	22,08	15,777	460	23,33	14,583
23	490	22,085	15,773	490	23,335	14,578
24	520	22,09	15,768	520	23,335	14,578
25	550	22,095	15,763	550	23,335	14,578
26	580	22,10	15,758	580	23,34	14,573
27	610	22,10	15,758	610	23,34	14,573
28	640	22,11	15,748	640	23,34	14,573
29	670	22,11	15,748	670	23,345	14,569
30	700	22,11	15,748	700	23,35	14,564

Początkowe wskazania:

1. ampułka zanurzona w wodzie - 22,83 kΩ

2. ampułka zanurzona w roztworze - 24,36 kΩ

Temperatura została wyliczona ze wzoru:

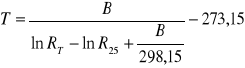
gdzie pod wartości B (stała materiałowa o wymiarze deg - stopień) i R₂₅ (znormalizowana rezystancja) podstawiono stałe dla białej sondy:

B = 3832 (deg)

R₂₅ = 14,65 (kΩ)

Minimalna (praktycznie znikoma) zmiana temperatury w okresie głównym jest potwierdzeniem prawa Hessa:

„ciepło reakcji chemicznej (w warunkach izobarycznych lub izochorycznych) nie zależy od drogi, którą biegnie reakcja, a jedynie od stanu początkowego i końcowego reakcji”.

Wyliczenia do pierwszej części ćwiczenia (ampułka z kwasem w wodzie):

Molowe ciepła rozpuszczania kwasu siarkowego w zależności od rozcieńczenia

	∞	20000	8000	4000	1000	600	200	100	50	20	10
Q (kJ/mol)	92,39	87,95	85,52	83,00	78,19	76,80	74,37	73,49	72,78	71,40	66,20

Wyliczam liczbę moli kwasu siarkowego w pierwszej ampułce:

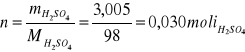
Na 1 mol kwasu siarkowego przypada 1111 moli wody. Znając molowe ciepła rozpuszczania kwasu w zależności od rozcieńczenia ( tabelka powyżej) można określić ciepło jakie powstało w reakcji:

Q_rozp.≈ 78,19

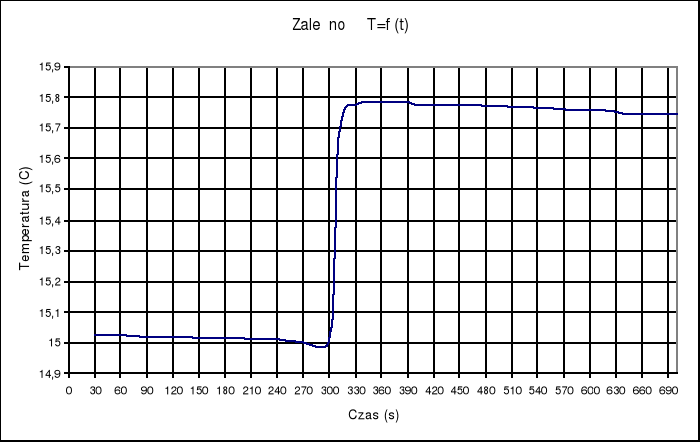
Wartość (Δt + ∑v) można wyznaczyć graficznie ( co zostało wykonane na wykresie poniżej) ale tą sumę można wyliczyć z zależności:

(Δt + ∑v)= T_II - T_I

gdzie: T_I - końcowa temperatura okresu początkowego

T_II - początkowa temperatura okresu końcowego

Powyższe wartości zostały wyliczone i umieszczone w tabeli na stronie 2.

(Δt + ∑v)= T_II - T_I = 15,777 - 15,004 = 0,773

Na podstawie wzoru (*) zawartego na stronie 1. wyliczam pojemność cieplną układu:

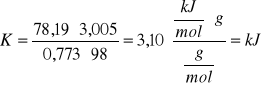
Pojemność cieplna jest wartością stałą dla konkretnego układu, dlatego też powyższa wartość zostanie wykorzystana w dalszych obliczeniach.

Wyliczenia do drugiej części ćwiczenia (ampułka z kwasem w roztworze):

Podobnie jak w części pierwszej należy wyliczyć wartość (Δt + ∑v).

(Δt + ∑v)= T_IV - T_III

gdzie: T_III - końcowa temperatura okresu początkowego

T_IV - początkowa temperatura okresu końcowego

Powyższe wartości zostały wyliczone i umieszczone w tabeli na stronie 2.

(Δt + ∑v)= T_IV - T_III = 14,583 - 13,613 = 0,97

Znając pojemność cieplną układu, masę kwasu siarkowego, jego masę molową i wartość (Δt + ∑v) można wyliczyć ciepło zobojętnienia:

W wykonanym ćwiczeniu miały miejsce dwa procesy o różnych efektach cieplnych, dlatego też ilość ciepła jakie wydzieliło się w kalorymetrze jest sumą ciepła rozpuszczania i ciepła zobojętnienia :

Q = Q_rozp. + Q_zob.

Q = 78,19 + 141,67

Q = 219,86

3. Wnioski

Proces zobojętniania mocnej zasady za pomocą mocnego kwasu jest w istocie relacją pomiędzy jonami H⁺ a OH^- z utworzeniem słabo zdysocjowanej cząsteczki wody:

H⁺ + OH^- → H₂O

Efekt cieplny tej reakcji wynosi około 13,7 kcal (57359). Wielkość ta praktycznie jest niezależna od rodzaju mocnej zasady i mocnego kwasu.

W ćwiczeniu został użyty słaby kwas, który w stanie równowagi pozostaje mieszaniną kwasu, jonów wodorowych oraz sprzężonej z tym kwasem zasady:

H₂SO₄ → 2H⁺ +SO₄^2-

Jeżeli w procesie zobojętniania zostanie użyta słaba zasada lub słaby kwas, to obserwowany efekt cieplny różni się znacznie od powyższej wartości, jaka jest podana dla mocnego kwasu i mocnej zasady. Wynika to stąd, że podczas zobojętniania słabego kwasu musi towarzyszyć proces dysocjacji tego kwasu.

2. Ampułka z kwasem w roztworze wodorotlenku sodu:

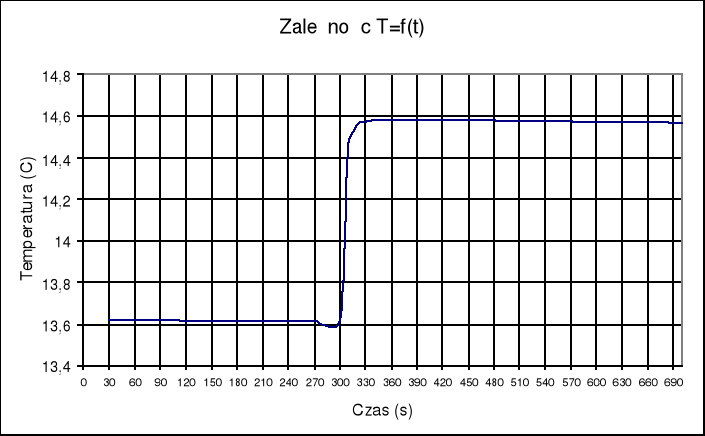
Ewa Nogawska Pomiary kalorymetryczne

---