Nr æw. 203	Data			Wydzia³ Elektryczny		Semestr III		Grupa I-1
Prowadz¹ca:				Przygotowanie		Wykonanie		Ocena

Temat: Wyznaczanie pojemnoœci kondensatora za pomoc¹ drgañ relaksacyjnych.

1. PojemnoϾ kondensatora.

Kondensatorem nazywamy uk³ad dwóch ok³adek metalowych dowolnego kszta³tu rozdzielonych dielektrykiem. W stanie na³adowania na ka¿dej z ok³adek znajduje siê ³adunek elektryczny Q o przeciwnym znaku, a miêdzy ok³adkami napiêcie U. Pojemnoœæ kondensatora to stosunek ³adunku do napiêcia:

.

Pojemnoœæ kondensatora zale¿y od jego kszta³tu, rozmiarów, wzajemnej odleg³oœci ok³adek i od rodzaju zastosowanego dielektryka.

2. £adowanie kondensatora

Pjoemnoœæ C ³aduje siê poprzez do³¹czenie SEM do obwodu zawieraj¹cego szeregowo po³¹czone opór R i pojemnoœæ C (prze³¹cznik w pozycji 'a'), natomiast roz³adowanie przez od³¹czenie SEM od obwodu (prze³¹cznik w pozycji 'b').

W dowolnym momencie procesu ³adowania na ok³adkach znajduje siê ³adunek q, a w obwodzie p³ynie pr¹d i. Zgodnie z II prawem Kirchhoffa spadki napiêæ na kondensatorze i oporniku s¹ kompensowane przez SEM Ÿród³a:

.

Po zró¿niczkowaniu tego równania i uwzglêdnieniu zwi¹zku i=dq/dt otrzymamy:

.

Jest to równanie ró¿niczkowe o zmiennych rozdzielonych. Po obustronnym sca³kowaniu otrzymujemy rozwi¹zanie:

,

gdzie i0 jest sta³¹ ca³kowania okreœlon¹ przez warunki pocz¹tkowe.

W dowolnej chwili napiêcie na kondensatorze wynosi Uc=-Ri i zmienia siê w czasie zgodnie z równaniem:

Po dostatecznie d³ugim czasie kondensator zostaje na³adowany ca³kowicie. Praktycznie dla t, Uc0 kondensator uwa¿a siê za na³adowany, gdy t=5RC.

3. Roz³adowywanie kondensatora

Pr¹d i napiêcie roz³adowywania wynosz¹ odpowiednio:

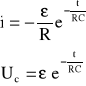
Wielkoœæ RC wystêpuj¹c¹ w powy¿szych równaniach nazywa siê sta³¹ obwodu (ma ona wymiar czasu). Okreœla ona prêdkoœæ ³adowania i roz³adowywania obwodu.

Jeœli w obwodzie RC do³¹czymy równolegle do kondensatora neonówkê wówczas wystêpuj¹ w obwodzie niesymetryczne wzrosty i spadki napiêæ na kondensatorze nazywane drganami relaksacyjnymi.

4. Drgania relaksacyjne

Polegaj¹ one na tym, ¿e napiêcie na kondensatorze, ³adowanym ze Ÿród³a, roœnie napiêcie a¿ do pewnej wartoœci Uz (napiêcia zap³onu), kiedy to zapala siê neonówka. Neonówka posiada ma³y opór, wiêc kondensator szybko siê roz³adowuje, a¿ napiêcie osi¹gnie wartoœæ napiêcia gasniêcia Ug (neonówka gaœnie). Znów nastêpuje ³adowanie kondensatora, jego roz³adowanie i tak dalej. Poniewa¿ opór jarz¹cej siê neonówki jest bardzo ma³y to czas roz³adowania stanowi ma³y u³amek ca³ego okresu i mo¿emy przyj¹æ, ¿e okres drgañ relaksacyjnych jest rówy czasowi ³adowania kondensatora od napiêcia Ug do Uz

W pierwszym cyklu ³adowania napiêcie U0 zostanie osi¹gniête po czasie t0, zatem

, gdzie:

U0 jest napiêciem Ÿród³a.

Pisz¹c podobne równanie dla chwili t0+T:

znajdujemy wzór na okres:

.

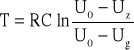
Ostatecznie zastêpuj¹c logarytm naturalny z powy¿szego równania (sta³y dla danej neonówki i danego napiêcia) przez K otrzymujemy:

.

Zatem okres drgañ relaksacyjnych jest wprost proporcjonalny do pojemnoœci i oporu.

5. Zasada pomiaru

By obliczyæ pojemnoœc kondensatorów najpierw nale¿y wyznaczyæ sta³¹ K. W tym celu u¿ywamy znanych oporników oraz kondensatora wzorcowego (dekadowego) o znanej pojemnoœci. Okres mierzymy za pomoc¹ sekundomierza (licz¹c iloœæ np. 20 b³ysków neonówki).

Nastêpnie pod³¹czaj¹c do obwodu szukane pojemnoœci mo¿emy obliczyæ ich wartoœci.

Pomiary

1. Pomiar wartości stałej K

W tabeli podany został czas 20 okresów [s]

pojemność [uF] rezystancja [MΩ]	czas 20 okresów [s]	stała K
C = 0,6 R = 16,5	9,38	0,047
	9,25	0,042
	9,36	0,045
	9,42	0,049
	9,20	0,041
C = 0,7 R = 9,9	7,17	0,051
	7,44	0,054
	7,40	0,053
	7,38	0,053
	7,26	0,052
C = 1 R = 13,2	13,06	0,049
	12,89	0,048
	12,93	0,048
	13,10	0,050
	13,12	0,051
średnia wartość stałej		0,048

Błąd stałej K otrzymujemy z pochodnej cząstkowej, przyjmując następujące niedokładności:

ΔT = 0,5 s ;

ΔR = 2%;

ΔC = 20%.

ΔK = 0,006

pojemność [uF] rezystancja [MΩ]	czas 20 okresów [s]	pojemność badana [uF]
C1 R = 16,5	4,40	0,18
	4,34	0,18
	4,21	0,17
	4,30	0,18
	4,10	0,16
C2 R = 9,9	6,00	0,53
	5,60	0,54
		5,30	0,53
		5,90	0,55
		6,03	0,53
		6,64	0,52
C2 R = 13,2	6,31	0,49
	6,14	0,49
	6,22	0,50
	6,08	0,49
	7,50	0,48
C2 R = 16,5	7,47	0,48
	7,54	0,50
	7,40	0,50
	7,32	0,49
	8,55	0,50
C3 R = 6,6	8,80	0,89
	8,82	0,89
	8,64	0,88
	8,95	0,90
	11,04	0,91
C3 R = 9,9	11,15	1,05
	11,10	1,06
	10,98	1,00
	10,89	1,02
	13,87	1,04
C3 R = 13,2	13,91	1,11
	13,82	1,12
	13,98	1,10
	14,01	1,13
	14,05	1,14
wartość średnia C1		0,18
wartość średnia C2		0,51
wartość średnia C3		1,11

ΔK = 0,006

Błędy obliczone dla poszczególnych kondensatorów metodą różniczki zupełnej wynoszą:

ΔC1 = 0,03 uF

ΔC2 = 0,09 uF

ΔC3 = 0,13 uF

Pojemności badanych kondensatorów wynoszą odpowiednio:

C1 = ( 0,18 + 0,03 ) uF,

C2 = ( 0,51 + 0,09 ) uF,

C3 = ( 1,11 + 0,13 ) uF.

Wnioski

Pojemność kondensatorów otrzymana w toku ćwiczenia zbliża się do wartości znamionowych podanych na kondensatorach:

C1 = 0,22 uF;

C2 = 0,47 uF;

C3 = 1,00 uF.

Rozbieżność spowodowana jest przede wszystkim znaczną tolerancją wartości pojemności sięgającą 20%, a ponadto zmianą właściwości fizycznych kondensatora po upływie dłuższego czasu.

pojemnoœæ szukana	opór R 3,3 [M]
[F]	1	2	3	4	5
0,4	0,305	0,280	0,274	0,272	0,273
0,5	0,328	0,287	0,278	0,279	0,280
0,6	0,330	0,297	0,292	0,294	0,295
0,7	0,327	0,313	0,310	0,310	0,293

Zatem œrednia wartoœæ K wynosi:

a b³¹d K (3odchylenie standardowe) wynosi:

czyli mo¿na przyj¹æ, ¿e K=0,2960,057

wyznaczanie pojemnoœci kondensatorów

czas 20 okresów [s]

pojemnoœæ wzorcowa	opór R 3,3 [M]
	1	2	3	4	5
Cx1	6,13	9,28	13,10	18,09	21,84
Cx2	10,88	19,40	27,32	37,13	46,44
Cx3	24,16	43,00	65,34	87,03	107,96

T=0,01 [s]

obliczanie Cxi

Stosuj¹c wzór:

otrzymujemy, po zaokr¹gleniu, odpowienio [F]:

pojemnoœæ wzorcowa	opór R 3,3 [M]
	1	2	3	4	5
Cx1	0,314	0,238	0,224	0,232	0,224
Cx2	0,557	0,497	0,466	0,476	0,476
Cx3	0,124	0,110	0,112	0,111	0,111

Widaæ ¿e wyniki w pierwszej kolumnie mo¿na odrzuciæ jako obarczone b³êdem grubym--widocznie ludzkie oko nie jest w stanie wystaczaj¹co dok³adnie "wy³apaæ" b³ysków w takim tempie

Zatem œrednie wartoœci Cxi wynosz¹ [F]:

,

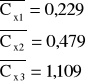
a b³êdy Cxi (3wspó³cz.St-Fischodchylenie standardowe) wynosz¹ [F]:

.

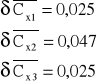
Zatem wyniki ostateczne to:

Cx1=0,2290,025 [F]

Cx2=0,4790,047 [F]

Cx3=1,1090,025 [F]

7. Wnioski i uwagi

Otrzymane wartoœci s¹ w pe³ni zgodne z danymi podanymi przez producenta kondensatorów, które wynosz¹:

Cx1=0,2220% [F]

Cx2=0,47 K [F]

Cx3=1 K [F]

gdzie K oznacza pewien przedzia³ tolerancji.

Do wykonywania pomiarów iloœci b³yœniêæ neonówki przydatny by³by czujnik podobny do tego w æwiczeniu wyznaczania przyspieszenia ziemskiego za pomoc¹ wahade³: rewersyjnego i matematycznego (101).

---