Płyn-ośrodek który ulega odkształceniom postaciowym a także objętościowym. Przez płyn rozumie się ciecz jak i gaz. Ciecz jest nieściśliwa, gaz jest ścisliwy. Ciecz nie ulega odkształceniom objętosciowym. Płyn to ośrodek ciągły.

Liczba Knutsena- stosunek średniej drogi swobodnej cząsteczki do charakterystycznego wymiaru opływowego.

- jeżeli
to strukturę molekularną pomijamy.

Element płynu- duża objętość w stosunku do średniej drogi swobodnej płynu z drugiej jednak strony mała w stosunku do elementu opływowego. Posiada własności makroskopowe.

W mechanice płynów modeluje się przepływy płynów rzeczywiste i doskonałe.

Płyn doskonały- nie lepki, nie ściśliwy, nie przewodzący ciepła.

Pole fizyczne- obszar w którym każdemu elementowi przypisana jest funkcja miejsca i czasu F=F(x,y,z,t)-pole nieustalone trójwymiarowe.

Pola- ustalone, nieustalone, stacjonarne, niestacjonarne, 1-2-trójwymiarowe,jednorodne, niejednorodne.

Własności płynów:

1.Gęstość płynu- m- masa ,
-objętość,
- gęstość średnia.

Dla płynu nieściśliwego gęstość jest stała. Gęstość może być funkcją ciśnienia, temperatury i czasu.

2.Ściśliwość- miara odkształcalności płynu spowodowana zmianą ciśnienia . współczynnik ściśliwości
.

lub
lub

-stosunek przyrostu objętości przez objętości podzielone przez zmianę ciśnienia.

3.Rozszerzalność objętościowa- miara odkształcalności płynu wywołana zmianą temperatury.

lub

4.Lepkość- miara tarcia wewnętrznego ,zdolność do przenoszenia naprężeń stycznych.

Dynamiczny wsp. lepkości

Prawo Newtona-
dn- elementarna wysokość szczeliny.

Rys.

Siły działające na płyn

Rys.

dσ-elementarna powierzchnia,
-elementarna objętość.

Siła masowa- objętościowa-odniesiona do jednostki masy.

Siła powierzchniowa- odniesiona do jednostki powierzchni.

współrzędne siły masowej

siła jednostkowa powierzchniowa.

siła bezwładności masowa może być wyrażona przez
,siła bezwładności powierzchniowa:

Statyka płynów

Równowaga płynów

Rys.

;

;
;
-Równania EULERA w statyce płynów, wiążą gęstość, pole sił masowych oraz pole ciśnień.

-wektor jednostkowy.

-to samo w zapisie wektorowym (równanie EULERA). Słuszne w dowolnym układzie odniesień.

Inna postać równowagi płynów (mnożone odpowiednio przez dx dy dz).

;
;

-różniczka zupełna.

- wtedy pole jest potencjalne.

U-potencjał jednostkowy sił pól masowych.

;
;

-równanie równowagi płynów.

Jeżeli p=const. to dp=0, dU=0, U=const- równanie powierzchni ekwipotencjalnej stałego potencjału. Siły masowe działające w polu ekwipotencjalnym są prostopadłe.

Równowaga względna i bezwzględna płynu.

Rys.

g-jednostkowa siła grawitacyjna.

⇒
;
;

X=Y=0, Z=g ⇒
;

p=p(Z);
;
⇒

z=0, p=p₀, c=p₀

-rozkład ciśnienia po objętości płynu w naczyniu. Wzór manometryczny.

Równowaga względna

Rys.

Układ x, y, z jest związany z układem(tak samo jak on się obraca).

;

p=const.⇒

X=B_X, Y=B_Y, Z=-g, X=ω²x, Y=ω²y, ω²xdx+ω²ydy-gdz=0

;

r=0, z=z₀ ⇒
-równanie względne cieczy. Równanie powierzchni ekwipotencjalnej (swobodnej powierzchni cieczy w tym naczyniu).

Parcie płynu na ściany płaskie i zakrzywione

-wektor jednostkowy.

Wypadkowa parcia p.:

Moment układu parcia.:

Parcie na ścianę płaską

Rys.

S_C-środek ciężkości

S_P-środek parcia.

Płaszczyzna swobodna cieczy w zbiorniku OXY

Ściana jest nachylona pod pewnym kątem (ηξζ)

;

W płaszczyźnie ściany ζ=0 ⇒ z=ξsinα

;
-moment statyczny.

⇒
⇒
-definicja parcia na ścianę płaską.

-ciśnienie hydrostatyczne.

Moment układu parcia.

;

;
;

D - moment odśrodkowy dewiacji

z twierdzenia Steinera

Parcie na ściany zakrzywione

Rys.

Wypadkowa parcia na ściany zakrzywione

;

;

;

G-ciężar

-odległość od środka ciężkości

-ciśnienie hydrostatyczne słupa cieczy określone w środku ciężkości

Pływanie ciał- stateczność pływania.

Pływanie ciał całkowicie zanurzonych w cieczy

Rys.

- ponieważ powierzchnia rzutu jest taka sama z obu stron ciśnienie też się nie zmienia

ale

- objętość elipsoidy

W-wypór hydrostatyczny

warunek równowagi : siła wyporu jest zrównoważona przez ciężar

W = G

gęstość ciała = gęstość cieczy

↓ W < G

↑ W > G

Środek ciężkości -S_c

Środek wyporu -S_W

RYS:

S_w=S_c - równanie obojętne, nic się nie dzieje-niestateczność pływania

M_p—moment prostujący

Jeżeli S_w był powyżej S_c to ciało powraca do poprzedniego położenia

M-moment przewracający

Jeżeli S_w poniżej S_c równowaga chwiejna-niestateczność

Pływanie częściowo zanurzonych w cieczy.

RYS:

Po wychyleniu objętość części zanurzonej nie zmieniła się :

M- punkt metacentryczny - przecięcie osi pływania z W'

a- odległość środka ciężkości od środka wyporu w warunkach równowagi

m- jest miarą stateczności pływania

kiedy m>0 - równowaga trwała (stateczność pływania)

kiedy m<0 - równowaga chwiejna (niestateczność)

kiedy m=0 - równowaga obojętna

M_p=W'l=W⋅l=ρ⋅g⋅τ⋅l=ρ⋅g⋅τ_z⋅ (m+a)sindϕ

Siła wyporu elementarna dW=ρ⋅g⋅dτ=ρ⋅g⋅z⋅dσ

dM=dW⋅x=dW⋅z⋅tgdϕ

dM=ρ⋅g⋅z²⋅tg(dϕ)⋅dσ

dM=ρ⋅g⋅z²⋅dσ⋅dϕ

M_p=ρ⋅g⋅dϕ⋅∫∫_σz²dσ

ρ⋅g⋅τ_z(m+a)dϕ=ρ⋅g⋅dϕ∫∫z²dσ

minimalny moment bezwładności przekroju pływania

J_min=∫∫_σz²dσ ;

a-odległość środka ciężkości od środka wyporu

τ_z-objętość zanurzonej części obiektu

ELEMENTY KINEMATYKI PŁYNU

Metoda Lagranga

RYS.

;
;

V = V_xi +V_yj + V_zk

x₀,y_0,z_o - zmienne Lagranga

;
;

wykorzystywana jest w zagadnieniach nieustalonego przepływu

Metoda Eulera - polega na obserwacji stałego punktu w przestrzeni

Rys.

- pochodna substancjalna pola prędkości (pochodna materiałowa)

- pochodna lokalna mówi jak zmienia się wektor prędkości po czasie

- pochodna konwekcyjna pola prędkości - określa zmianę prędkości po przejściu z punktu do punktu(punkty leżą bardzo blisko)

Linia prądu - linia do której styczny jest wektor prędkości ( też linia po której porusza się element płynu)

- wektorowy wyraz linii prądu

;
;

W równaniu linii prądu czas t jest parametrem

Tor elementu płynu - linia po której porusza się element płynu

- równanie toru elementu płynu

;

W ruchu ustalonym tor elementu płynu pokrywa się z linią prądu.

Ruch lokalny płynu

Rys.

T - tensor prędkości względnej

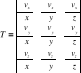
Każdy tensor można rozłączyć na symetryczną i antysymetryczną.

Obszar płynny - obszar, który składa się z tych samych elementów płynu i z upływem czasu może zmieniać swój kształt.

- tensor prędkości deformacji

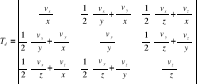
T₀ - tensor antysymetryczny

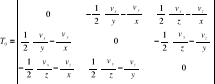
Te tensory można dla uproszczenia zapisać krócej:

;
;
;

Poszczególne wyrazy to są prędkości deformacji:

- objętościowych płynów (na głównej przekątnej)

- postaciowej (pozostałe)

T₀ - tensor obrotu sztywnego:

;
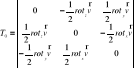
- wektor prędkości obrotowej

Tensor obrotu sztywnego wiąże się z obrotem płynu potraktowanego jako bryła sztywna.

Prędkość dowolnego obszaru jest równa:

- I równanie Helsholza

- wektor prędkości deformacji

- prędkość kątowa zdefiniowana w punkcie P'

- prędkość obrotu sztywnego

Przepływy potencjalne:

- Φ - potencjał prędkości

- funkcja skalarowa zależna od składowych prędkości i czasu

;
;

Potencjalne przepływy to takie dla których pole prędkości równe jest gradΦ, a rotv=0 ( rotacja pola prędkości jest równa 0, przepływ jest bezwirowy)

Przepływ wirowe:

dla których:
;
- wektor wiru

linia wirowa - linia do której styczny w każdym jej punkcie jest wektor wiru

Podstawowe równania mechaniki płynu - wynikają z 3 zasad: zasady zachowania masy, pędu, energii

Zasada zach. masy - w zamkniętym układzie masa nie może powstawać ani zanikać)

Obszar kontrolny - wyznaczony przez te same punkty przestrzeni, który z upływem czasu kształt nie ulega zmianie.

W ogólności dla płynu ściśliwego - gazu:

W ruchu ustalonym:

Jeż. płyn jest nieściśliwy (czy gęstość=const) divV=0 (zarówno w ruchu ustalonym jak i nieustalonym)

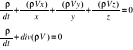
Równania ciągłości przepływu:

div(ρV)=0

divV=0

Np. dla cieczy: masa cieczy doprowadzana do obszaru kontrolnego musi być równa masie cieczy wypływającej z ob. kontrol.

Z zasady zach. pędu: Zmiana pędu musi być równa impulsowi wszystkich sił

gdzie: F- pole jednostk. siły masowej

S-tensor naprężeń w płynie (w ogólności lepkim płynie)

Składowe na przekątnej głównej to naprężenie normalnej w płynie a pozostałe to naprężenia styczne.

Równanie pędu naprężeń:

Tensor naprężeń w cieczy doskonałej (nie lepkiej - nie występują naprężenia styczne):

Równanie konstytutywne (Newtona):

Podstawowym równaniem z którego możemy określić pole prędkości, pole ciśnień, musimy dołączyć do równania ciągłości przepływu, równanie konstytutywne płynu.

gdzie: T_d-Tensor pręd. deform., μ-dynam. współ. lepkości, T-tensor

Dla płynu ściśliwego, lepkiego:

Dla płynu nieściśliwego:

Równania Naviera-Stokes'a:

Zasada zachowania energii

1.Zmiana energii jast przyczyną pracy i sił mechanicznych

2.Energia wytworzona wewnątrz obszaru płynnego

3.Energia doprowadz. z zewnątrz do obsz. płynnego

Energia całkowita jest sumą en. kinetycznej płynu i en. wewnętrznej

Ec=Ek+Ew

v-prędkość

Ew ~ T, (proporcjonalnie do temp.)

Ew = C_vT C_v - ciepło właściwe przy stałej obiętości

raca sił powierzchniowych (δ) i obiętościowych (τ)

Obszar płynny:

całkowa forma równania energii:

- Energia doprowadzona

gdzie q_r,t= strumień ciepła zależny też od czasu; p_n=wektor jednostkowych sił powierzchniowych działających na ten obszar; s- tensor naprężeń w płynie lepkim

Tw. Gaussa i Ostogradzkiego:

po przekształceniach:

jeżeli
to wnętrze jest równe 0.

z zasady zachowania pędu:

Zmiana energii kinetycznej równa jest pracy sił mechanicznych.

- dysypacja energii mach.

-postać równania doskonałego płynu Lamba-Gromedi (jest podstawą do całki

Corshea-Lagranga)

w ruchu ustalonym:

-całka Corshera-Lagranga dla ruchu ustalonego nie zależy od czasu

Całka Bernuliego

-równanie Eulera (pomnożymy przez ds)

Założenia dla całki Bernuliego

1.
-gradU-gradient pola potencjalnego

2.

-p jest funkcją P

w efekcie przemnożenia otrzymujemy

-różniczka

-jeżeli różniczka =0 to wnętrze =const

-całka Bernuliego taka sama jak całka Coushera-Lagranga dla ruchu ustalonego

v-predkość średnia przepływu jednomiarowego

Dla pola grawitacyjnego

Jeżeli rzecz dotyczy płynu doskonałego

-ale ρ=const dla cieczy =>P=p/ρ

wprowadzamy to do całki Bernuliego

/ρ ;

-równanie Bernuliego przepływu doskonałego jednowymiarowego

-dla płynu doskonałego

RYS.

opis; w przypadku jednowymiarowym przepływów rzeczywistych linia (stała) w góry ulega pochyleniu

w wyniku naprężeń dynamicznych występują straty

Dla przepływów rzeczywistych:

-wys. strat liniowych(strat tarcia, strat na długości przewodów)

-wys. strat miejscowych (lokalne, związane ze zmianą przekroju)

λ-wsp. straty liniowej

Re- liczba Reynoldsa

k- chropowatość bezwzględna

k/d- chropowatość względna

W przypadku laminarnego przepływu rzeczywistego

RYS.

układ bilogarytmiczny

-dla przepływu turbulentnego

ζ-wsp. straty lokalnej może być zależny od liczby Reynoldsa ζ=ζ(Re) (przeważnie dla przepływu laminarnego)

Dynamika płynu lepkiego

- r-nie ciężkości przepływu cieczy

- tw. Naviera-Stokesa

Określić pole prędkości w laminarnym lepkim przepływie płaskim między dwoma nieruchomymi powierzchniami jak:

rys

;

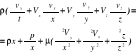
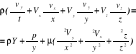
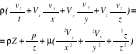
dla przepływu płaskiego nie ma „Z”

wektor sił masowych równa się „0”

linia prądu - linia do której wektor prędkości jest styczny

zakładamy, że linie prądu są równoległe to V_y=0 wtedy otrzymujemy (kreślić następnie wszystko co z V_y)

;

zakładamy, że przepływ jest ustalony w czasie

a więc zostanie tylko:

;

po scałkowaniu

i jeszcze raz

warunki brzegowe

V_x=0 y=±h

⇒

;

;

Płaski profil Poissona

rys

Zakładamy, że ścianki się poruszają to wracając do war. brzegowych

V_x=U₁ ; y=h

V_x=U₂ ; y=-h

;

;

Zakładamy, że

; U₁>0; U₂=0

;

Płaski profil Q

rys

Określić rozkład prędkości w laminarnym ustalonym lepkim przepływie w rurze kołowej wymuszonej stałym gradientem prędkości

rys

założenia

1^o F=0 pole sił masowych

2^o
Przepływ ustalony w czasie

3^o linie pędu są w przybliżeniu równoległe do V_x, V_y =0

4^o Przepływ lepki laminarny jest ustabilizowany

;

z poprzednich równań układu zostanie tylko

;

V_z=V_z(x,y)

Układ cylindryczny (r,o,z)

;

całkujemy

⇒

C musi być, bo inaczej na środku rury prędkość dążyłaby do nieskończoności

V_z=0 kiedy r=R

⇒

⇒

⇒

G- pole powierzchni przekroju

rys

;

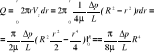
Bezwymiarowa postać równania Naviera-Stokse'a

Równanie Naviera - Stoksa dla cieczy lepkiej ( w postaci wymiarowej)

=
;
=
;
=
; p =
;
;

- składowa siły masowej

;
L - charakt. Wymiar

;

/

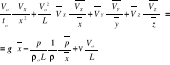
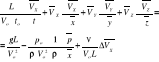
z pomocą liczb kryterialnych

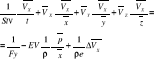
za pomocą wektorowych - bezwymiarowych postać:

Liczba Stranchla... jest to stosunek pewnych sił

Str =↕
↕

Liczba Fruga- jest to stosunek

=↕
↕

Liczba Eulera(Eu)

Eu=

Liczba Reynoldsa

Re=

LAMINARNA WARSTWA PRZYSCIENNA

rownanie Eulera opisulace przeplyw plynu doskonalego.

Rownanie Prandtla

I-obszar na powierzchni(warstwa przyscienna)

II-obszar przeplywu który modelujemy jako przeplyw plynu doskonalego

Rys.

Zał. Ustalony plaski przeplyw

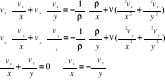
1.

2.Sily bezwładności są tego samego rzędu co siły lepkości.

-prędkość w przepływie niezakluczonym rzędu

x=0(L)
jest rzedu L

;
;

;

;

⇒ gradient ciśnienia w poprzek warstwy przyściennej jest stały

;

Oderwanie warstwy przyściennej

Warunki brzegowe do powierzchni

O profilu prędkości decyduje gradient ciśnienia

Wypukły wklęsło-wypukły

Rys.

Trzy możliwości prędkości:

rys:

y = 0 ;
y = 0 ;
y = 0

Przepływy turbulentne

f = f (x, y, z, t)

Możemy zapisać to równanie za pomocą zasady uśrednień.

;
;

Rys.

;
;

Miarą turbulencji nie jest średnia z kwadratu fluktracji; Miarą turbulęcji jast wsp. intensyw. turbulętnej:

Ostateczne rów. ruchu turbulencyjnego w postaci wektorowej:

T_T - tensor naprężeń turbulętnych

hipotezy zamykające równania naprężeń turbulentych

---