Wydział Techniki	Uniwersytet Śląski	Data
				19-11-1998
Zakład Systemów Informatycznych
Sprawozdanie numer 1.	Paweł Kopaczek	Ocena ................
		Piotr Kopaczek	Podpis ...............

Zestaw numer 6.

Zadanie 1.

W przypadku analizy par bitów mnożnika w metodzie Booth'a ( I wariant ) konieczne jest dopisanie zera na najmniej znaczącej pozycji. Udowodnij, że niespełnienie tego wariantu nie da poprawnego wyniku dla mnożenia tą metodą.

Zadanie 2.

Następujące pary liczb dodaj w kodzie ZM, ZU1, ZU2.

a) X=
Y= −

b) X=
Y=

Zadanie 3.

Następujące pary liczb pomnożyć stosując I wariant algorytmu Booth'a:

a) X=
Y=

b) X= −
Y=

Zadanie 4.

Następującą parę liczb podziel stosując metodę nierestytucyjną:

X=
Y=

Odpowiedź 1.

,
,

,

,

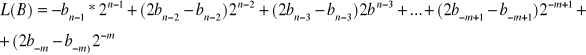
Brakuje pary dla tego iloczynu (
), dlatego trzeba dopisać 0, czyli:
(to jest poprawka dla I metody Booth'a).

U=L(A)*L(B);

L(B)=
;

U=L(A)*
;

Odpowiedź 2.

Dodawanie w ZM wykonuje się zgodnie z poniższą tabelką.

Operacja	Bity znakowe an-1, bn-1	Operacje wykonywane	Znak sumy
Dodawanie	Jednako- we znaki	Z^*=A^*+B^*	Zn-1= an-1
	Różne znaki	Z^*=A^*−B^*	Zn-1= an-1 w = 0
					Zn-1= an-1 w = 1

Uwaga:

Z^*,A^*,B^* − bity liczbowe.

Z_n-1,a_n-1,b_n-1 − bity znakowe.

w = 1 − wynik uzyskujemy w kodzie U₂, zapisać w ZM a na końcu ustalić bity

znakowe.

k + 1 pozycji obowiązuje w trzech kodach.

a) X=
Y= −

k+1 pozycji

X=(0.0,0001111)_ZM X=(0.0,00011110)_ZM

Y=(1.0,000101)_ZM Y=(1.0,00010100)_ZM

⊕

,00011110

− ,00010100 w = 0

,00001010

−−−−2³−2¹− =
=

Bit znakowy ustalamy według tabelki. Z_n-1= a_n-1 w = 0, więc bit znakowy otrzymanej liczby równa się 0.

Otrzymana liczba równa się (0.0,00001010)_ZM =
₁₀=
₁₀.

b) X=
Y=

k+1 pozycji

X=(0.0,000001011)_ZM X=(0.0,0000010110)_ZM

Y=(0.0,10011)_ZM Y=(0.0,1001100000)_ZM

,0000010110

+ ,1001100000 w = 0

,1001110110

,2⁸−− 2⁶2⁵2⁴−2²2¹− =
=
=

Bit znakowy ustalamy według tabelki. Z_n-1= a_n-1 w = 0, więc bit znakowy otrzymanej liczby równa się 0.

Otrzymana liczba równa się (0.0, 1001110110)_ZM==
₁₀=
₁₀.

W przypadku ZU₁ operacja dodawania jest wykonywana łącznie z bitami znakowymi. I w przypadku wystąpienia przepełnień są one uwzględniane poprzez dodanie jedynki do najmniej znaczącej pozycji.

a) X=
Y= −

k+1 pozycji

X=(0.0,0001111)_ZM X=(0.0,00011110)_ZM X=(0.0,00011110)_ZU1

Y=(1.0,000101)_ZM Y=(1.0,00010100)_ZM Y=(1.0,11101011)_ZU1

0.00011110

+ 1 --> [Author:PK] .11101011

10.00001001

+ 1

0.00001010

−.−−−−2³−2¹− =
=

Otrzymana liczba równa się 0.0,00001010 =
₁₀=
₁₀

b) X=
Y=

k+1 pozycji

X=(0.0,000001011)_ZM X=(0.0,0000010110)_ZM X=(0.0,0000010110)_ZU1

Y=(0.0,10011)_ZM Y=(0.0,1001100000)_ZM Y=(0.0,1001100000)_ZU1

0.0000010110

+ 0.1001100000

0.1001110110

−_.2⁸−− 2⁶2⁵2⁴−2²2¹− =
=
=

W przypadku ZU₂ operacja wykonywana jest łącznie z bitami znakowymi a przepełnienia są ignorowane.

a) X=
Y= −

k+1 pozycji

X=(0.0,0001111)_ZM X=(0.0,00011110)_ZM X=(0.0,00011110)_ZU1 X=(0.0,00011110)_ZU2 Y=(1.0,000101)_ZM Y=(1.0,00010100)_ZM Y=(1.0,11101011)_ZU1 Y=(1.0,11101100)_ZU2

0.00011110

+ 1 --> [Author:PK] .11101100

10.00001010

przepełnienie jest ignorowane

0.00001010

−.−−−−2³−2¹− =
=

Otrzymana liczba równa się 0.0,00001010 =
₁₀=
₁₀

b) X=
Y=

k + 1 pozycji

X=(0.0,000001011)_ZM X=(0.0,0000010110)_ZM X=(0.0,0000010110)_ZU2

Y=(0.0,10011)_ZM Y=(0.0,1001100000)_ZM Y=(0.0,1001100000)_ZU2

0.0000010110

+ 0.1001100000

0.1001110110

−.2⁸−− 2⁶2⁵2⁴−2²2¹− =
=
=

Otrzymana liczba równa się 0.0, 1001110110 =
₁₀=
₁₀.

Odpowiedź 3.

I wariant Booth'a dotyczy mnożenia w kodzie ZU₂.

Badamy kolejne ostatnie pary bitów mnożnika.

1).Jeżeli badana para jest kombinacją 1 0 to do iloczynu częściowego ( który na

początku jest wyzerowany) odejmujemy mnożną i przesuwamy wynik o jedno

miejsce w prawo.

2).Jeżeli badana para jest kombinacją 0 1 to do iloczynu częściowego dodajemy

mnożną i przesuwamy wynik o jedno miejsce w prawo.

3).Jeżeli badana para jest parą o jednakowych liczbach 00 11 to nic nie robimy

a później przesuwamy w prawo o jedno miejsce.

4).Jeżeli w skład pary wchodzi bit znakowy to nie wykonujemy przesunięcia.

a) X=
Y=

X = (0.00111)

Y = (0.10101)

0.00111

* 0.101010

0.00000

− 0.00111

1.11001

1.111001

+ 0.00111

0.000111

0.0000111

− 0.00111

1.1101011

1.11101011

+ 0.00111

0.00100011

0.000100011

− 0.00111

1.110110011

1.1110110011

+ 0.00111

0.0010010011

Otrzymana liczba równa się (0.0010010011) =
₁₀=
₁₀.

b) X= −
Y=

X = (1.01)_ZM = (1.11)_ZU2

Y = (0.111)_ZM = (0.1110)_ZM

1.11

∗ 0.1110

0.00

−1.11

0.01

0.001

0.0001

0.00001

+ 1.11

1.11001

Otrzymana liczba równa się (1.11001)_ZU2 =
₁₀=
₁₀.

Odpowiedź 4.

Metoda nierestytucyjna jest metodą dzielenia w ZU₂ .

Aby można było podzielić liczby w metodzie nierestytucyjnej musi być spełniony warunek |A | < |B |, (A - dzielna, B − dzielnik ).

Metoda ta polega na badaniu znaku dzielnika i kolejnej reszty częściowej. Jeżeli znaki te są zgodne to odejmujemy dzielnik od przesuniętej w lewo reszty częściowej. Jeżeli znaki ich są różne, to dodajemy dzielnik do przesuniętej w lewo kolejnej reszty częściowej. Jeżeli bity znakowe są równe, to bit ilorazu równa się 1. Jeżeli bity znakowe nie są równe, to bit ilorazu równa się 0. Do otrzymanego wyniku dodajemy poprawkę równą = − 1+2^{- n}, gdzie n - numer ostatniej reszty z dzielenia.

X=
Y=

X=(0.0001011)_ZU2

Y=(0.0001)_ZU2

0.0001011

−0.0001 q₀ = 1

r₀=0.0000011

0.000011

− 0.0001 q₁ = 1

r₁= 1.111111

1.11111

+ 0.0001 q₂ = 0

r₂= 0.00001

0.0001

− 0.0001 q₃ = 1

−−−−−

Do uzyskanej liczby (1.101) dodajemy poprawkę -1+2^-4= -
= (1.0001)_ZU2

1.101

+1.0001

0.1011

Otrzymana liczba równa się (0.1011) =
₁₀=
_10.

1

9

---