Wydział GiK spec. Poligrafia |
Zespół nr . |
1. 2. 3. |
Ocena z przygotowania:
|
Piątek 11.15. - 14.00. |
Ocena ze sprawozdania: |
Data : |
Zaliczenie: |
Prowadzący: |
Podpis: |
.STATYSTYCZNY CHARAKTER ROZPADU PROMIENIOTWÓRCZEGO.
Promieniotwórczość naturalna została odkryta w 1896 roku przez H.Becquerela. Kilka lat później stwierdzono, że liczba rozpadów w jednostce czasu czystej substancji promieniotwórczej maleje wykładniczo z czasem. W roku 1905 zinterpretowano ten fakt jako dowód na to, że rozpad promieniotwórczy ma charakter stochastyczny (statystyczny).
Prostą konsekwencją przypadkowości rozpadu promieniotwórczego powinno być istnienie fluktuacji statystycznych, czyli rozrzutu zmierzonych wielkości wokół wartości średniej. wyniki pomiarów rzeczywistej aktywności dowolnej próbki nie będą układały się idealnie na krzywej wykładniczej. Rozrzut punktów wokół krzywej wykładniczej jest spowodowany w tym wypadku nie tyle błędami doświadczalnymi, (chociaż i one mogą wystąpić), lecz właśnie statystycznym charakterem mierzonej wielkości. W przypadku jąder o dużym okresie połowicznego rozpadu, naszym badaniom dostępny jest tylko niewielki wycinek krzywej wykładniczej, który możemy przybliżyć prostą o zerowym nachyleniu.
Jest to równoważne założeniu o stałej aktywności preparatu. Statystyczny charakter rozpadu promieniotwórczego spowoduje, że aktywność preparatu o bardzo dużym okresie połowicznego rozpadu będzie stała na granicy fluktuacji statystycznych.
W związku z tym wszystkim mamy prawo oczekiwać, że dla jąder o dostatecznie długim okresie połowicznego zaniku rozkład pr-wa danej liczby rozpadów w jednostce czasu będzie zgodny z teoretycznym rozkładem pr-wa zdarzeń przypadkowych.
Nie wszystkie procesy stochastyczne maj --> [Author:IS] --> [Author:IS] ą jednak tę samą naturę. Zastanówmy się nad różnicą w statystycznym charakterze rozpadu promieniotwórczego i ruchów Browna. Chaotyczne ruchy zawiesiny ciała stałego w cieczy można nie tylko opisać przy pomocy rachunku prawdopodobieństwa, ale rozpatrując szerszy układ, to znaczy cząsteczki cieczy, wskazać przyczynę nagłych zmian kierunku ruchu zawiesiny. W próbce jąder promieniotwórczych nie możemy przewidzieć, które z jąder ulegnie w danej chwili rozpadowi. Fakt ten jest niezależny od żadnych czynników zewnętrznych, ani od historii próbki. Zjawiska zachodzące podczas rozpadu promieniotwórczego mają charakter indeterministyczny.
Charakteryzując próbkę możemy mówić tylko o średnim czasie życia jądra do chwili rozpadu. Związek między średnim czasem życia a stałą rozpadu jest następujący:
τ=1/λ ,gdzie λ-stała rozpadu.
Średnie czasy życia jąder promieniotwórczych mieszczą się w zakresie wartości:
od milionowej części sekundy do miliardów lat.
CEL ĆWICZENIA:
Tematem ćwiczenia jest statystyczny charakter rozpadu promieniotwórczego. Niestety istniejące warunki pozwalają nam jedynie zbadać rozkład częstotliwości rozpadów promieniotwórczych próbki o okresie połowicznego rozpadu dostatecznie długim w porównaniu z czasem obserwacji (pozwala to na założenie stałej aktywności próbki).
Rozkładem opisującym ściśle częstotliwość zdarzeń przypadkowych jest rozkład dwumianowy.
Jednak w naszym przypadku rozkładu tego nie możemy zastosować ze względu na nieznajomość całkowitej liczby jąder promieniotwórczych znajdujących się w próbce. Będziemy natomiast porównywać wyniki doświadczalne (histogramy doświadczalne) z przybliżonymi rozkładami teoretycznymi: dla małej średniej liczby zdarzeń z rozkładem Poissone'a, dla dużej średniej liczby zdarzeń z rozkładem Gaussa.
Sprawdzenie natomiast, czy doświadczalny rozkład zajścia danej liczby rozpadów w jednostce czasu jest zgodny z którymś z podanych wyżej rozkładów teoretycznych, można dokonać przy pomocy testu .
PRZYPOMNIENIE WIADOMOŚCI Z RACHUNKU PR-WA.
ROZKŁAD DWUMIANOWY
Dokonujemy n doświadczeń losowych. W rezultacie każdego z nich może zajść zdarzenie A z pr-wem p oraz zdarzenie przeciwne do A z pr-wem q=p-1. Wobec tego zmienna losowa X może przybierać wartości k=0,1,2,3,...,n, przy czym równość X=k oznacza, że w n doświadczeniach zdarzenie A zaszło dokładnie k razy. Funkcja pr-wa tej zmiennej dana jest wzorem:
i nosi nazwę rozkładu dwumianowego.
ROZKŁAD POISSONE'A
Rozkład Poissone'a otrzymujemy jako przybliżenie rozkładu dwumianowego przy przejściu do granicy z liczbą prób n i założeniu , że pr-wo pojedynczego zdarzenia p jest małe, co implikuje warunek, że k<<n. Po przekształceniach i kolejnych przybliżeniach otrzymujemy rozkład Poissone'a:
Oznaczmy iloczyn np literą m i połóżmy k=x, wówczas rozkład Poissone'a przyjmie postać:
Wyrażenie to określa pr-wo zarejestrowania x rozpadów promieniotwórczych w obranej jednostce czasu przy ustalonej wartości m, gdzie m to wartość oczekiwana rozkładu Poissone'a.
Wartość oczekiwana jest równa z definicji :
gdzie xi-zmienna losowa; p(xi)-pr-wo jej wystąpienia.
Jak wynika z powyższych zależności, rozkład Poissone'a jest wyznaczony jednoznacznie przez tylko jeden parametr: wartość oczekiwaną, jest więc rozkładem jedno-parametrycznym. Wraz ze wzrostem m rozkład Poissone'a staje się coraz bardziej rozmyty, zarazem też coraz bardziej symetryczny.
Badając próbkę n jąder promieniotwórczych, wartość oczekiwaną rozkładu Poissone'a można dobrze przybliżyć przez średnią liczbę rozpadów zarejestrowanych w naszym eksperymencie w jednostkowym przedziale czasu, tzn. np=m=Nśr.
Odchylenie standartowe w rozkładzie Poissone'a równe jest δ=, co tłumaczy wzrost szerokości rozkładu ze wzrostem średniej.
Z powyższego wynika, że jeżeli mamy do czynienia ze zmienną losową podlegającą rozkładowi Poissone'a, to gros wyników będzie się zawierać w przedziale . W przypadku, gdy przeprowadzamy eksperyment polegający na zliczaniu wielkości przypadkowych i gdy mamy do dyspozycji tylko jeden pomiar -N, to błąd jego na poziomie jednego odchylenia standartowego wynosi .
Jest to tzw. błąd statystyczny, wynikający ze statystycznego charakteru mierzonej wielkości.
Rozkład Gaussa
Rozkład teoretyczny Gaussa opisywany jest dwoma parametrami:
xśr - będące średnią arytmetyczną ilości rozpadów promieniotwórczych w jednostce czasu wzór nr 1
- dodatkowo każdy pomiar obarczony jest niepewnością wzór nr 2
σ - drugi parametr, jest to średnia niepewność pojedynczego pomiaru, określająca „szerokość” funkcji Gaussa. wzór nr 3
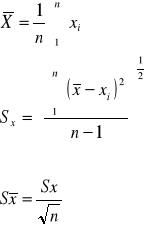
TEST
Test służy do ilościowej oceny zgodności serii pomiarowej z krzywą teoretyczną, która naszym zdaniem powinna opisywać dane zjawisko. Jeżeli krzywa teoretyczna będzie miała postać y=f(x), a serię pomiarów stanowić będzie l wartości wielkości yi zmierzonych przy ustalonych wartościach xi , to suma:
, gdzie δi-błąd mierzonej wielkości yi, jest wielkością dobrze oddającą odstępstwa wszystkich punktów eksperymentalnych od krzywej teoretycznej.
Spodziewana wielkość powinna być zbliżona do liczby składników sumy, gdyż wkład każdego z nich w poprawnie przeprowadzonym eksperymencie, jest rzędu 1.
Można udowodnić, że jeśli wielkość yi obarczona jest tylko błędami przypadkowymi
(z odchyleniem standartowym δi), to wielkość również podlega pewnemu rozkładowi pr-wa o gęstości:
,gdzie
k-liczba stopni swobody rozkładu (liczba niezależnych składników sumy)
Γ(k/2)- funkcja gamma Eulera.
Wartość oczekiwana wielkości jest właśnie równa liczbie stopni swobody k.
Wzór:
ulega pewnej modyfikacji, gdy badamy zgodność doświadczalnych rozkładów pr-wa liczby zdarzeń przypadkowych z rozkładem teoretycznie przewidywanym, np.(Poissone'a lub Gaussa).
Załóżmy, że przeprowadziliśmy n pomiarów, a zmienną niezależną x pogrupowaliśmy w i przedziałach. Wówczas wielkość yi musimy zastąpić liczbą ni, która jest liczbą zarejestrowanych przez nas zdarzeń typu xi. Wartość teoretyczna f(xi), przy spełnionym warunku:
będzie z kolei równa npi, gdzie pi jest obliczonym przez nas rozkładem teoretycznym.
Błąd wielkości ni, która jako liczba zdarzeń przypadkowych podlega rozkładowi Poissone'a, równy jest pierwiastkowi z wartości oczekiwanej: δi=npi, a więc:
W tym wypadku liczba stopni swobody, to liczba przedziałów l zmniejszona o jeden(ze względu na warunek normalizujący) oraz zmniejszona o liczbę parametrów s, jednoznacznie wyznaczających rozkład(dla rozkładu Poissone'a s=1, dla rozkładu Gaussa s=2).
Na podstawie tabeli rozkładumożna znaleźć poziom ufności P, jaki odpowiada otrzymanej ze wzoru wartości przy znanej liczbie stopni swobody.
A oto wyniki naszego doświadczenia, przedstawione w postaci załączonych histogramów.
Na pierwszym histogramie widzimy rozkład o małej średniej liczbie rozpadów w jednostce czasu (tzn. średnia wynosi 5 rozpady na 1 sekundę), z tego też powodu będziemy porównywać go z teoretycznym rozkładem Poissone'a. W pomiarze tym przeprowadziliśmy 662 pomiarów, a wyniki rozłożyły się następująco:
ILOŚĆ ROZPADÓW W JEDNOSTCE CZASU |
ILOŚĆ ZDARZEŃ Z DANĄ LICZBĄ ROZPADÓW |
0 |
9 |
1 |
39 |
2 |
82 |
3 |
106 |
4 |
107 |
5 |
109 |
6 |
101 |
7 |
46 |
8 |
23 |
9 |
26 |
10 |
7 |
11 |
4 |
12 |
3 |
SUMA: 662
Teraz obliczamy test dla rozkładu Poissone'a, używamy danych z powyższej tabeli:
x i |
n i |
(prawdopodobieństwo wg Poissona) pi |
(normalizacja ) pi*n |
Obliczenia testu x2 |
0 |
9 |
0,0109 |
7,2330 |
0,4317 |
1 |
39 |
0,0493 |
32,6685 |
1,2271 |
2 |
82 |
0,1114 |
73,7756 |
0,9168 |
3 |
106 |
0,1678 |
111,0721 |
0,2316 |
4 |
107 |
0,1895 |
125,4175 |
2,7046 |
5 |
109 |
0,1711 |
113,2925 |
0,1626 |
6 |
101 |
0,1288 |
85,2831 |
2,8965 |
7 |
46 |
0,0831 |
55,0273 |
1,4809 |
8 |
23 |
0,0469 |
31,0672 |
2,0948 |
9 |
26 |
0,0236 |
15,5909 |
6,9495 |
10 |
7 |
0,0106 |
7,0418 |
0,0002 |
11 |
4 |
0,0044 |
2,8914 |
0,4251 |
12 |
3 |
0,0016 |
1,0883 |
3,3583 |
|
∑ 662 |
|
|
22.8797 Suma testu x2 |
Średnia arytmetyczna ilości rozpadów w czasie 4,5 |
||||
Xi - liczba rozpadów rejestrowanych w ciągu 1 s.
N - ilość wszystkich pomiarów (662).
Ni - liczba pomiarów określonej liczby rozpadów.
Pi - pr-wo zarejestrowania liczby Xi rozpadów przewidywane zgodnie z rozkładem Poissone'a przy parametrze m=4,5.
N*Pi - przewidywana teoretycznie liczba rozpadów Xi.
Liczba stopni swobody w tym przypadku wynosi k=13 -1 -1 = 11.
Dla 11-stu stopni swobody wartość wynosi 24,7 , a więc < , co oznacza, że dla poziomu ufności P=0,01 hipoteza mówiąca, że nasze dane doświadczalne opisane są rozkładem Poissone'a, nie jest fałszywa.
W tym miejscu chcemy porównać rozkład doświadczalny o małej średniej liczbie zliczeń
Tym razem z rozkładem Gaussa (którego wartości obliczymy samodzielnie.
x i |
n i |
(prawdopodobieństwo wg Goussa) pi |
(normalizacja )pi*n |
Obliczenia testu x2 |
0 |
9 |
0,02 |
15,59 |
2,78 |
1 |
39 |
0,05 |
34,54 |
0,58 |
2 |
82 |
0,09 |
62,77 |
5,89 |
3 |
106 |
0,14 |
93,59 |
1,64 |
4 |
107 |
0,17 |
114,47 |
0,49 |
5 |
109 |
0,17 |
114,85 |
0,30 |
6 |
101 |
0,14 |
94,52 |
0,44 |
7 |
46 |
0,10 |
63,82 |
4,97 |
8 |
23 |
0,05 |
35,34 |
4,31 |
9 |
26 |
0,02 |
16,06 |
6,16 |
10 |
7 |
0,01 |
5,98 |
0,17 |
11 |
4 |
0,00 |
1,83 |
2,58 |
12 |
3 |
0,00 |
0,46 |
14,08 |
|
662 |
|
|
35,14 |
|
|
|
|
suma testu x2 |
Średnia niepewność pojedynczego pomiaru |
|
|
||
|
|
|
2,25 |
|
Średnia arytmetyczna ilości rozpadów w jednostce czasu |
|
|
||
|
|
|
4,5 |
|
Powyższe wyniki pokazuje załączony wykres.
Wszystkie dane są te same jedynie Pi - prawdopodobieństwo zarejestrowania liczby Xi rozpadów przewidywane jest zgodnie z rozkładem Gaussa
Liczba stopni swobody w tym przypadku wynosi k=13 - 1* - 2** = 10
* - tak jak wyżej zmniejszmy o 1 ze względu na warunek normalizacji
** - zmniejszenie o liczbę charakteryzujących rozkład parametrów ( czyli dla rozkłady Gaussa = 2 )
Dla 10-u stopni swobody wartość wynosi 23,2, a więc> co oznacza, że dla poziomu ufności P = 0,01 hipoteza mówiąca, że nasze dane doświadczalne opisywane są rozkładem Gaussa, jest fałszywa.
Wykonaliśmy drugą serię pomiarów dla dużej liczby zliczeń w jednostce czasu i porównaliśmy z teoretycznym rozkładem Gaussa. Wykres graficzny tego pomiaru dołączyliśmy na końcu, a oto wyniki naszych pomiarów:
Xi - liczba rozpadów rejestrowanych w ciągu 1 s.
N - ilość wszystkich pomiarów ( 595 ).
Ni - liczba pomiarów określonej liczby rozpadów.
Pi - pr-wo zarejestrowania liczby Xi rozpadów przewidywane zgodnie z rozkładem Gauss'a
N*Pi - przewidywana teoretycznie liczba rozpadów Xi.
Liczba stopni swobody w tym przypadku wynosi k=35-1-2=32.
Dla 32-uch stopni swobody nie można odczytać wartość natomiast dla 30-u stopni swobody wynosi 50,9 , a więc < , co oznacza, że dla poziomu ufności P=0,01 hipoteza mówiąca, że nasze dane doświadczalne opisane są rozkładem Gaussa , nie jest fałszywa.
Wyniki w tabeli na następnej stronie
x i |
n i |
(prawdopodobieństwo wg Goussa) pi |
(normalizacja )pi*n |
Obliczenia testu x2 |
24 |
1 |
0,00 |
0,29 |
1,75 |
25 |
2 |
0,00 |
0,49 |
4,69 |
26 |
0 |
0,00 |
0,80 |
0,80 |
27 |
1 |
0,00 |
1,27 |
0,06 |
28 |
1 |
0,00 |
1,97 |
0,48 |
29 |
1 |
0,00 |
2,96 |
1,30 |
30 |
2 |
0,01 |
4,32 |
1,24 |
31 |
5 |
0,01 |
6,12 |
0,20 |
32 |
10 |
0,01 |
8,41 |
0,30 |
33 |
10 |
0,02 |
11,23 |
0,14 |
34 |
16 |
0,02 |
14,57 |
0,14 |
35 |
24 |
0,03 |
18,35 |
1,74 |
36 |
24 |
0,04 |
22,45 |
0,11 |
37 |
20 |
0,04 |
26,66 |
1,67 |
38 |
25 |
0,05 |
30,75 |
1,08 |
39 |
40 |
0,06 |
34,45 |
0,90 |
40 |
42 |
0,06 |
37,46 |
0,55 |
41 |
51 |
0,07 |
39,57 |
3,30 |
42 |
52 |
0,07 |
40,58 |
3,21 |
43 |
33 |
0,07 |
40,42 |
1,36 |
44 |
29 |
0,07 |
39,10 |
2,61 |
45 |
34 |
0,06 |
36,72 |
0,20 |
46 |
30 |
0,06 |
33,49 |
0,36 |
47 |
28 |
0,05 |
29,66 |
0,09 |
48 |
26 |
0,04 |
25,51 |
0,01 |
49 |
19 |
0,04 |
21,31 |
0,25 |
50 |
13 |
0,03 |
17,28 |
1,06 |
51 |
13 |
0,02 |
13,61 |
0,03 |
52 |
13 |
0,02 |
10,41 |
0,65 |
53 |
7 |
0,01 |
7,73 |
0,07 |
54 |
8 |
0,01 |
5,58 |
1,05 |
55 |
6 |
0,01 |
3,90 |
1,12 |
56 |
6 |
0,00 |
2,66 |
4,21 |
57 |
2 |
0,00 |
1,75 |
0,03 |
58 |
1 |
0,00 |
1,12 |
0,01 |
|
595 |
|
|
29,53 |
|
|
|
|
suma testu x2 |
Średnia niepewność poj. pomiaru |
|
|
||
|
|
|
5,8 |
|
Średnia arytmetyczna ilości rozpadów w jednostce czasu |
|
|||
|
|
|
42,3 |
|
WNIOSKI:
Wyniki naszych pomiarów i wykresy dowiodły, że rozkład promieniotwórczy jest procesem przypadkowym. Wyraża się to tym, że wielokrotne pomiary aktywności, czyli liczby rozpadów zachodzących w jednostce czasu wykazują fluktuacje statystyczne wokół pewnej wartości średniej zmierzonej w ciągu bardzo długiego czasu. Jednak w warunkach laboratorium studenckiego nie możemy w pełni udowodnić wykładniczego zmniejszania się aktywności próbki, niezależności stałej rozpadu od czynników zewnętrznych i jej niezmienności w czasie. Rozkład częstości rozpadów promieniotwórczych rejestrowanych w stałej jednostce czasu był zgodny z teoretycznym rozkładem zdarzeń przypadkowych, a krzywe teoretyczne wykreślone na histogramach nie odbiegały znacznie od wartości wyznaczonych doświadczalnie.
Stosując różne rozkłady teoretyczne dla małej liczby zdarzeń, spróbowaliśmy potwierdzić słuszność założenia, że rozkład Poisson'a należy stosować dla małej liczby zdarzeń, a rozkład Gaussa dla dużej. Zastosowanie rozkładu Gaussa dla małej liczby zdarzeń było niesłuszne co bardzo szybko potwierdziło się testem .
10
Wyszukiwarka