Wykład 6
Zasady zmienności w dynamice układu punktów materialnych i ciała sztywnego
6.1 Pęd układu punktów materialnych (pęd główny):
![]()
UWAGA: to jest sumowanie wektorów a więc sumowanie geometryczne.
Zasada zmiany pędu głównego:
![]()
(i=1,...,n oraz k=1,...,n)
Suma wektorów sił zewnętrznych: ![]()
Zgodnie z III prawem dynamiki Newtona: ![]()
![]()
![]()
- wektor główny sił zewnętrznych (wektor wypadkowy).
Różniczkowa zasada zmiany pędu głównego:
Pochodna po czasie wektora pędu głównego jest równa wektorowi głównemu sił zewnętrznych działających na układ punktów materialnych.
Podobnie jak dla pojedynczego punktu, można wyprowadzić całkowitą zasadę pędu głównego.
Zasada ruchu środka masy układu punktów materialnych:
Z równości momentu statycznego środka masy układu punktów materialnych i sumy momentów statycznych wszystkich punktów tego układu:
![]()
![]()
M - całkowita masa układu punktów materialnych
![]()
- wektor przyspieszenia środka masy układu punktów materialnych
Środek masy układu punktów materialnych porusza się tak jak punkt o masie M pod wpływem wszystkich sił zewnętrznych działających na ten układ.
6.2 Praca i energia kinetyczna układu punktów materialnych:
Energia kinetyczna układu punktów materialnych. Twierdzenie Königa:
C- środek masy układu punktów materialnych.
![]()
![]()
![]()
Po przekształceniach otrzymujemy (twierdzenie Königa):
![]()
![]()
- energia kinetyczna środka masy układu punktów materialnych
Ew - energia kinetyczna układu punktów materialnych w jego ruchu względem środka masy C
Twierdzenie Königa: Energia kinetyczna układu punktów materialnych jest równa sumie energii kinetycznej, jaką miałby punkt materialny o masie całego układu, poruszający się z prędkością środka masy, oraz energii kinetycznej tego układu w jego ruchu względem środka masy.
6.3 Kręt główny (kręt układu punktów materialnych).
![]()
![]()
Zasada zmiany krętu głównego:
![]()
Z ostatniego równania wynikają następujące równania na współrzędne wektora krętu w układzie Oxyz
![]()
Mx, My, Mz - momenty sił zewnętrznych względem odpowiednich osi współrzędnych.
Jeśli na układ nie działają żadne siły zewnętrzne to Mx=My=Mz=0. Wówczas ma miejsce zasada zachowania krętu:
![]()
6.4 Pęd ciała sztywnego:
![]()
m - masa ciała sztywnego,
![]()
- prędkość środka masy ciała sztywnego
Zasada zmiany pędu ciała sztywnego:
![]()
![]()
![]()
- wektor wypadkowy sił zewnętrznych działających na środek masy ciała sztywnego
Zasada zmiany pędu ciała sztywnego:
Pochodna względem czasu wektora pędu ciała sztywnego jest równa wektorowi wypadkowemu sił zewnętrznych działającemu na środek masy tego ciała.
6.5 Energia kinetyczna ciała sztywnego i praca:
![]()
Energia kinetyczna ciała sztywnego w ruchu dowolnym.
![]()
![]()
![]()
- energia kinetyczna ruchu obrotowego względem chwilowej osi l,
![]()
- moment bezwładności ciała sztywnego względem l;
Il=const w ruchu obrotowym wokół stałej osi obrotu.
Energia kinetyczna ciała sztywnego w ruchu postępowym:
![]()
Energia kinetyczna ciała sztywnego w ruchu obrotowym wokół stałej osi:
![]()
Energia kinetyczna ciała sztywnego w ruchu płaskim:
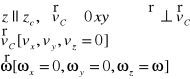
![]()
6.6 Kręt (moment pędu) ciała sztywnego:
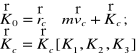
![]()
kręt środka masy ciała sztywnego względem bieguna 0;
![]()
kręt względem środka masy ciała sztywnego
Współrzędne wektora krętu w układzie C 123:
K1 =I1 ![]()
1 ; K2 =I2 ![]()
2 ; K3 =I3 ![]()
3
Zasada zmiany wektora krętu ciała sztywnego:
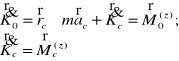
Kręt ciała sztywnego w ruchu obrotowym wokół stałej osi:
Jeśli prosta z jest osią obrotu ciała sztywnego to jego kręt (współrzędna) wynosi:
![]()
![]()
Zasada zmiany krętu:
![]()
Jeśli Mz = 0 to otrzymujemy zasadę zachowania krętu ciała sztywnego.
![]()
6.7 Dynamiczne równania ruchu ciała sztywnego:
Dynamiczne równania ciała sztywnego w ruchu dowolnym:
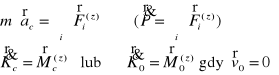
![]()
- suma sił czynnych i reakcji działających na ciało sztywne
Dynamiczne równania CS w ruchu postępowym:
![]()
Wniosek: Ruch postępowy ciała sztywnego jest równoważny ruchowi punktu.
Ciało sztywne swobodne w ruchu postępowym ma k=3 stopnie swobody (tak jak punkt).
Dynamiczne równania ruchu obrotowego wokół stałej osi. Reakcje dynamiczne łożysk:
L - dowolna stała oś obrotu ciała sztywnego
Ciało sztywne w ruchu obrotowym wokół stałej osi ma k=1 st. swobody.
Z zasady zmiany krętu ciała sztywnego dla ruchu obrotowego wokół stałej osi otrzymamy:
![]()
![]()
Stąd dynamiczne równanie ruchu obrotowego wokół dowolnej stałej osi l:
![]()
Uwaga: powyższe równanie nie zależy od sił reakcji w łożyskach, lecz tylko od sił czynnych zewnętrznych.
Reakcje dynamiczne łożysk:
AB = l
![]()
= const
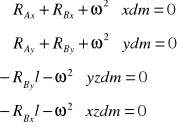
Po podstawieniu
![]()
otrzymujemy równania:
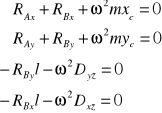
Stąd obliczamy 4 składowe reakcji dynamicznych łożysk:
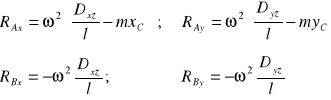
Całkowite reakcje dynamiczne łożysk A i B:
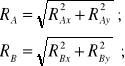
Podsumowanie:
Reakcje dynamiczne występują tylko w czasie ruchu ciała sztywnego, tzn. gdy ![]()
≠ 0
Jeśli oś obrotu ciała sztywnego jest jedną z głównych centralnych osi bezwładności, tzn. xc = yc = 0 oraz Dxz = Dyz = 0, to wtedy reakcje dynamiczne są równe zeru (RA = RB = 0).
Dwa przypadki wyrównoważenia:
1. Wyrównoważenie dynamiczne: RA = RB = 0, czyli kiedy oś obrotu jest jedną z głównych centralnych osi bezwładności, nazywamy ją wówczas osią swobodną.
2. Wyrównoważenie statyczne: xc = yc = 0 ale Dxy ≠ 0 i Dyz ≠ 0, oś obrotu jest wtedy osią centralną, lecz nie główną.
Reakcje dynamiczne natomiast tworzą parę sił:
![]()
Wzory pomocnicze przy obliczaniu reakcji dynamicznych:
C123 - układ głównych centralnych osi bezwładności,
Cxyz - układ osi centralnych
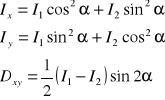
Wyszukiwarka