POLITECHNIKA ŚLĄSKA W GLIWICACH WYDZIAŁ ORGANIZACJI I ZARZADZANIA Katedra Podstaw Systemów Technicznych

Laboratorium z przedmiotu PODSTAWY METROLOGII

Ćwiczenie nr 3

Uśrednianie wyników pomiarów oraz szacowanie błędu wartości średniej

Wykonali	Piotr Gola Marek Gaura
Kierunek	ZIP
Grupa	2
Sekcja	1
Data	30.01.2008

Rok akademicki 2008/2009

Semestr zimowy

1. Celem naszego ćwiczenia było zrozumienie pojęcia dokładności pomiarów oraz zapoznanie się metodami wyznaczania błędów prostych i złożonych.

2. Ponieważ ćwiczenie składa się z dwóch odrębnych zadań do każdego z nich użyliśmy innych przedmiotów pomiarowych. W zadaniu pierwszym skorzystaliśmy ze stopera i wahadła matematyczne natomiast w zadaniu drugim skorzystaliśmy z 5 mierników uniwersalnych następujących typów:

• MASTECH MY 67

• DT 832

• DT 9208

• DT 9207

• DT 9205

3. a) W ćwiczeniu pierwszym należało zmierzyć po jakim czasie wahadło wychyli się 15-krotnie. Przeprowadziliśmy 10 pomiarów, z których otrzymaliśmy następujące wyniki:

L.p.	Czas (s)
1.	21,04
2.	21,6
3.	21,4
4.	21,6
5.	21,4
6.	22,2
7.	21,6
8.	22,0
9.	22,2
10.	22

Na podstawie dokonanych pomiarów możemy określić średnią wartość mierzonego czasu oraz oszacować średni błąd kwadratowy.

Wartość średnia serii pomiarowej zdefiniowana jest jako:

gdzie n to liczba dokonanych pomiarów a
to suma ich kolejnych wartości.

Suma wartości mierzonego czasu wynosi 217,04 s. Tak, więc korzystając ze wzoru możemy obliczyć średnią wartość mierzonego czasu.

Możemy stwierdzić, że przeciętny czas trwania jednego pomiaru
wynosił t = 21,7 s.

Błąd kwadratowy serii pomiarowej zdefiniowany jest następująco:

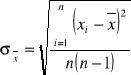
W celu wykonania dokładnych obliczeń należy wykonań pomocniczą tabelkę:

21,04	-0,66	0,4356
21,6	-0,1	0,01
21,4	-0,3	0,09
21,6	-0,1	0,01
21,4	-0,3	0,09
22,2	0,5	0,25
21,6	-0,1	0,01
22	0,3	0,9
22,2	0,5	025
22	0,3	0,9
	Razem:	2,9456

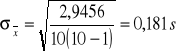
Zatem czas średni wynosi: t = (21,7 ± 0,181) s

b) W ćwiczeniu drugim dokonaliśmy pomiaru napięcia za pomocą sześciu różnych mierników, otrzymaliśmy następujące wyniki:

L.p.	Pomiar napięcia	Miernik	Zakres
1.	1,938V	MASTECH MY 67	automat.
2.	1910mV (1,910V)	DT 832	2000mV (2V)
3.	1,874V	DT 9208	2V
4.	1,85	DT 9207	20V
5.	1,8	DT 9205	200V
6.	1	DT 9205	1000V

Znając wartości zmierzonego napięcia możemy wyznaczyć błąd bezwzględny dla każdego pomiaru., wartość średnią oraz błąd kwadratowy.

Błąd bezwzględny:

MASTECH MY 67:

ΔU₁ = ± 0,5%W ± 2D

ΔU₁ =

DT 832:

ΔU₂ = ± 0,5%W ± 2D

ΔU₂ =

DT 9208:

ΔU₃ = ± 0,5%W ± 2D

ΔU₃ =

DT 9207:

ΔU₄ = ± 0,5%W ± 2D

ΔU₄ =

DT 9205:

ΔU₅ = ± 0,5%W ± 2D

ΔU₅ =

DT 9205:

ΔU₆ = ± 0,8%W ± 2D

ΔU₆ =

Wartość średnia serii pomiarowej zdefiniowana jest jako:

gdzie n to liczba dokonanych pomiarów a
to suma ich kolejnych wartości.

Suma wartości mierzonego napięcia wynosi 10,372V. Tak, więc korzystając ze wzoru możemy obliczyć średnią wartość mierzonego napięcia.

Wartość przeciętna mierzonego napięcia wynosi U = 1,729V

Błąd kwadratowy serii pomiarowej zdefiniowany jest następująco:

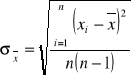
W celu wykonania dokładnych obliczeń należy wykonań pomocniczą tabelkę:

1,938V	0,209	0,043681
1,910V	0,181	0,032761
1,874V	0,145	0,021025
1,85	0,121	0,014641
1,8	0,071	0,005041
1	-0,729	0531441
	Razem:	0,64859

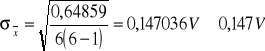
Zatem napięcie średnie wynosi: U = (1,729 ± 0147)V

4

---