Nr ćwiczenia : 12	Temat ćwiczeń: Wyznaczanie przerwy energetycznej	Ocena z teorii:
Nr zespołu:	Imię i nazwisko: Jacek Zańko	Ocena zaliczenia ćwiczenia:
Data ćwiczenia: 02.03.2004	Wydział: EAIiE, rok IB, grupa7, EiT	Uwagi:

Przerwa energetyczna - Struktura energetyczna ciała stałego - w ciałach stałych energie elektronów ograniczone są do pewnych poziomów, które z kolei należą do pewnych pasm. Między poszczególnymi pasmami występują tzw. przerwy energetyczne. Przebywanie elektronu w takiej przerwie jest niemożliwe. Pasma wypełnione elektronami walencyjnymi noszą nazwę pasm walencyjnych (lub podstawowych), a pasma wypełnione częściowo lub puste (odpowiadające większym energiom) - przewodnictwa. Elektrony znajdujące się w pasmach całkowicie zapełnionych nie wnoszą żadnego wkładu w przewodnictwo elektryczne, ze względu na brak wolnych, dozwolonych stanów energetycznych. W pasmach przewodnictwa (częściowo zapełnione lub puste) istnieją dozwolone puste stany energetyczne i elektrony pod wpływem np. zewnętrznego pola elektrycznego mogą przenosić się na nie, zatem biorą udział w przewodnictwie elektrycznym. Przewodniki są materiałami o niecałkowicie obsadzonym paśmie podstawowym lub o zlewających się ze sobą pasmach: podstawowym i przewodzenia. Jeżeli najwyższe zapełnione pasmo walencyjne jest oddzielone przerwą od najniższego pasma przewodnictwa to mamy do czynienia z

• półprzewodnikiem (przerwa energetyczna Eg<2 eV - elektrony mogą łatwo „przeskoczyć" przerwę energetyczną np. czerpiąc energię z fluktuacji termicznych) lub

• izolatorem (przerwa energetyczna Eg>2eV).

Mechanizm przewodzenia prądu oparty na gruncie teorii pasmowej - gdy przykładamy do przewodnika bądź półprzewodnika napięcie, elektrony są przyspieszane polem elektrycznym, pobierajac od tego pola energię, co na wykresie energetycznym przedstawić można jako przemieszczanie się elektronu ku górze w obrębie pasma. Taką możliwość mają oczywiście tylko elektrony z pasma przewodnictwa, bo pasma walencyjne są zapełnione. W którymś momencie elektron ulega oczywiście rozproszeniu, zderząjac się z jonem sieci krystalicznej. Traci przy tym energię, czyli "spada" na dół pasma, skąd znowu może być przyspieszany itd. Energię od pola elektrycznego elektron pobiera w spósob ciągły, dlatego może się dzięki niej przemieszczać w ramach pasma, a nie może przeskoczyć do następnego pasma, gdyż to wymaga dużej porcji energii (większej niż szerokość pasma).

Różnice w strukturze energetycznej dla metalu, izolatora i półprzewodnika.

• Dielektryki charakteryzują się tym, że szerokość przerwy energetycznej jest duża, a przy tym wszystkie pasma są w całkowicie zapełnione.

• Przewodniki z kolei mają bardzo wąskie pasma wzbronione tak, że czasami pasma przewodnictwa praktycznie zachodzą na siebie i elektrony z górnych pasm swobodnie mogą zmieniać swoją energię.

• Półprzewodniki charakteryzują się pośrednią wartością przerwy energetycznej. Prowadzi to do tego, że część elektronów z najwyższego pasma może przeskoczyć przez pasmo wzbronione do następnego pasma dozwolonego, w którym jest wiele wolnych poziomów i w ramach którego elektron może przemieszczać się już swobodnie. W temperaturze bliskiej zera absolutnego półprzewodnik zachowuje się tak jak izolator, to znaczy ma bardzo dużą oporność. Po prostu wszystkie pasma są zapełnione. Aby elektron mógł przeskoczyć do pasma przewodnictwa musi uzyskać energię wyższą niż szerokość przerwy energetycznej. Najprościej dostarczyć mu tę energię podgrzewając półprzewodnik lub np. oświetlając go światłem o odpowiednio dużej energii kwantów.

Przerwę energetyczną Eg można wyznaczyć na kilka sposobów:

1. Z zależności przewodnictwa elektrycznego od temperatury

2. Z zależności przewodnictwa elektrycznego od energii padającego promieniowania elektromagnetycznego

3. Z pomiarów współczynnika absorpcji promieniowania elektromagnetycznego w

zależności od energii tego promieniowania.

Absorpcja Elektron może zwiększyć swoją energię jedynie kosztem absorpcji promieniowania elektromagnetycznego. Jeżeli na półprzewodnik padają fotony o energii wystarczającej na przeniesienie elektronu z pasma walencyjnego do pasma przewodnictwa to są one silnie absorbowane. Zatem w widmie absorpcyjnym półprzewodnika można wyróżnić gwałtowny wzrost współczynnika absorpcji w pobliżu energii hn równej szerokości przerwy energetycznej Eg. Efekty tego oddziaływania można prześledzić stosując tzw. materiałowe równania Maxwell'a. Rozwiązaniem tych równań jest równanie fali rozchodzącej się w ośrodku absorbującym:

gdzie n jest rzeczywistym współczynnikiem załamania, a wielkość ℵ jest to współczynnik ekstyncji, który opisuje absorpcję światła. Drugi czynnik ekspotencjalny opisuje tłumienie fali wraz z odległością. Natężenie fali jest wprost proporcjonalne do średniej czasowej z kwadratu pola elektrycznego (I ~ E²). Zatem stosunek natężenia promieniowania padającego do promieniowania, które przebyło pewną drogę wyraża się:

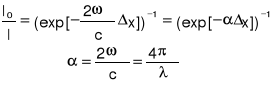
 to współczynnik absorpcji. Definicją jego jest: dI= - I dx

dl to zmiana natężenia fali na odległości dx.

Wyrażenie na energetyczną zależność współczynnika absorbcji dla przejść optycznych w obszarze krawędzi absorbcji dane jest:

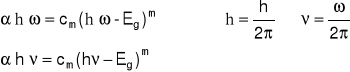
gdzie c_m - stała zależna od rodzaju przejścia

Chcąc określić wartość przerwy energetycznej Eg z pomiarów optycznych należy wyznaczyć wartość współczynnika absorpcji , który z kolei można wyznaczyć z pomiarów współczynnika transmisji T, który jest stosunkiem natężenia fali elektromagnetycznej przechodzącej przez próbkę do natężenia fali padającej na próbkę. Transmisję światła można przedstawić jako:

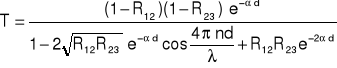
gdzie
jest współczynnikiem odbicia światła na granicy powietrze-warstwa, a
jest współczynnikiem odbicia światła na granicy warstwa-podłoże, n_s jest współczynnikiem załamania podłoża, d grubość warstwy. Złożoność wyrażenia na transmisje wynika z faktu, iż światło przechodzące przez cienką warstwę ulega nie tylko absorpcji ale także wielokrotnym odbiciom na powierzchniach rozdzielających różne ośrodki optyczne. Ponad to w widmie transmisji występują maksima i minima interferencyjne. Zjawisko interferencji zachodzi ponieważ grubość warstwy półprzewodnika jest porównywalna z długością fali promieniowania elektromagnetycznego padającego na badaną próbkę.

Współczynnik załamania n można wyznaczyć korzystając z minimów i maksimów interferencyjnych transmisji podstawiając za cos() odpowiednio jego wartość maksymalną i minimalną. Z powstałych równań otrzymujemy:

gdzie: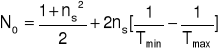

Mając wyznaczone R₁₂ i R₂₃ (niezależne od energii) oraz zmierzoną wartość transmisji T=T(hν), można wyliczyć dla każdej energii (długości fali) wartość współczynnika absorpcji korzystając ze wzoru:

Wzór ten jest słuszny w obszarze dużej absorpcji.

Zjawisko fotoelektryczne wewnętrzne i zewnętrzne

• Promieniowanie wychodzące z wnętrza bloków ma zawsze większe natężenie niż promieniowanie ze ścian bocznych (rysunek),

• Dla danej temperatury emisja promieniowania wychodzącego z otworów jest identyczna dla wszystkich źródeł promieniowania, pomimo że dla zewnętrznych powierzchni te wartości są różne,

• Emisja energetyczna promieniowania ciała doskonale czarnego (nie jego powierzchni) zmienia się wraz z temperaturą według prawa Stefana

σ - uniwersalną stała (stała Stefana-Boltzmana) równa 5.67·10^-8 W/(m²K).

Dla zewnętrznych powierzchni to empiryczne prawo ma postać:

gdzie zdolność emisyjna e jest wielkością zależną od substancji i, co jeszcze bardziej skomplikowane, od temperatury.

R_λ dla ciała doskonale czarnego zmienia się z temperaturą tak jak na rysunku poniżej. Długość fali dla której przypada maksimum emisji jest odwrotnie proporcjonalna do temperatury ciała.

---