Temat: Badanie zależności oporu metalu i półprzewodnika od temperatury
Grupa: L02	Imię i nazwisko: Ewelina Jankowska	Data wykonania ćwiczenia: 19.04.2011

1.Opór, oporność i przewodność - relacje między tymi wielkościami.

W roku 1826 Georg Simon Ohm stwierdził doświadczalnie, że wartość prądu jednokierunkowego I, przepływającego przez metalowy przewodnik jest wprost proporcjonalna do napięcia U, wynikającego z różnicy potencjałów początku V1 i końca V2 przewodnika (U = V1 - V2):

I ~ U;

Zależność ta jest powszechnie nazywana prawem Ohma. współczynnik proporcjonalności R nosi nazwę rezystancji (oporu elektrycznego, oporności).

Powyższa zależność może być również przedstawiona w postaci I =G∙U

gdzie:

i wówczas jest to konduktancja (przewodność elektryczna).

Jednostka rezystancji jest om [1 Ω], a jednostka konduktancji - simens [1 S].

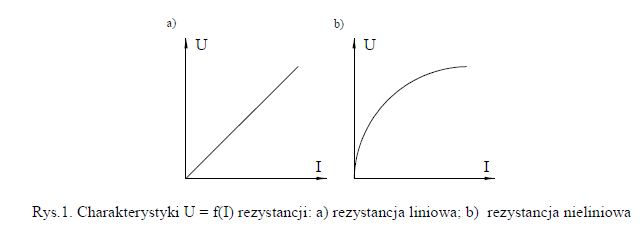
Związek określający opór elektryczny z zależności od napięcia i prądu można przedstawić graficznie jako charakterystykę napięciowo-prądową oporności. Gdy wartość rezystancji jest niezależna od prądu i napięcia, wówczas charakterystyka napięciowo-prądowa jest linią prostą i nosi nazwę rezystancji liniowej. Wtedy przebiegi czasowe prądu i napięcia są do siebie proporcjonalne. Jeżeli charakterystyka napięciowo-prądowa

nie jest linią prostą, to rezystancja zależy od prądu i napięcia i nazywa się

rezystancją nieliniową.

Rezystancja przewodu jest tym większa, im większa jest jego długość l i im mniejszy przekrój poprzeczny s.

Współczynnik proporcjonalności jest stałą, której wartość zależy od rodzaju materiału

przewodu. Stała ta, nazywa sie opornością właściwą. Wielkość odwrotna nazywa sie przewodnością właściwą.

Zgodnie z powyższym równaniem, rezystancja materiału ma, w zależności od konduktywności, postać następującą:

2. Na czym polega przepływ prądu elektrycznego w metalach i półprzewodnikach?

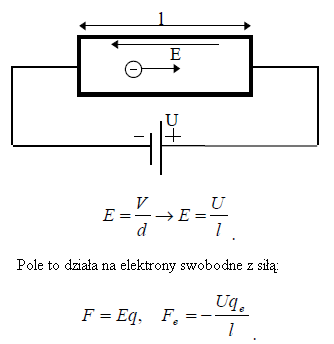
Wszystkie metale są dobrymi przewodnikami elektryczności. Struktura krystaliczna metali jest taka, że każdy atom wnosi do sieci krystalicznej co najmniej jeden elektron, który nie jest związany z żadnym konkretnym atomem. W przewodniku istnieją więc tzw. elektrony swobodne lub elektrony przewodnictwa. Jeżeli taki przewodnik umieścimy w polu elektrycznym, to na elektrony działać będzie siła elektryczna powodująca ich przemieszczanie wzdłuż przekroju przewodnika. To przemieszczenie nazywamy prądem elektrycznym. Zakładamy, że metalowy przewodnik o długości l i polu przekroju poprzecznego S połączony jest ze źródłem o napięciu U.

W kryształach półprzewodników (np. krzem, german, arsenek galu) wszystkie atomy są związane w przestrzennej siatce krystalicznej z tak samo oddalonymi atomami. Takie wiązanie nazywamy wiązaniami kowalencyjnymi, natomiast elektrony- elektronami walencyjnymi. W temperaturze bliskiej zeru bezwzględnemu wszelkie elektrony walencyjne biorą udział w wiązaniach międzyatomowych - brak wolnych elektronów odpowiedzialnych za przepływ prądu. Razem ze wzrostem temperatury kryształu, energia cieplna jest gromadzona głównie w formie energii drgań atomów. Pewna ilość elektronów walencyjnych uzyskuje energię dostateczną do przezwyciężenia sił powiązań z atomami. Wówczas tworzą się elektrony swobodne, natomiast w obszarach zwolnionych przez elektrony tworzą się tzw. dziury. Elektrony swobodne są ładunkami ujemnymi, natomiast dziury - dodatnimi. Gdy ulokujemy rozpatrywany kryształ w polu elektrycznym nastąpi uporządkowany ruch elektronów oraz pozorny ruch dziur w przeciwnych kierunkach. Prąd ten posiada jednak bardzo niewielką wartość, ponieważ elektrony swobodne stanowią małą ilość elektronów walencyjnych. Istotną własnością półprzewodników jest to, że nośniki ładunków elektrycznych w sieci krystalicznej są w stanie przemieszczać się nie tylko na skutek działającego pola elektrycznego, ale również na skutek cieplnych drgań sieci krystalicznej. Przesuwając się w taki sposób z jednego miejsca (gdzie jest ich bardzo dużo ) do kolejnego miejsca (gdzie jest ich niewiele ) produkują prąd dyfuzyjny.

3. Opisać model pasmowy przewodnika, półprzewodnika i dielektryka.

Materiały pod względem przewodnictwa elektrycznego dzielą się na 3 grupy: przewodniki, półprzewodniki i nieprzewodniki, zwane również dielektrykami, materiałami izolacyjnymi. Klasyfikacja ta związana jest z wewnętrzną budową atomową ciał i ze stanami energetycznymi nośników prądów w tych materiałach.

Podstawą podziału materiałów ze względu na ich właściwości elektryczne jest tzw. pasmowy układ energetyczny. W najogólniejszym przypadku istnieją w materiałach trzy pasma: przewodnictwa, podstawowe i zabronione.

W paśmie przewodnictwa elektron może poruszać się pod wpływem czynników zewnętrznych (temperatura, pole elektryczne).

W paśmie podstawowym (walencyjnym) na elektron działają tylko siły wynikające
z ruchu elektronów po ich orbitach oraz siły elektryczne działające między ujemnymi elektronami i dodatnim jądrem.

Pasmo zabronione znajduje się między pasmem podstawowym i pasmem przewodnictwa.

Wielkość pasma zabronionego określa się w elektronowoltach (energia uzyskana przez elektron przebywający bez przeszkód drogę pomiędzy punktami o różnicy potencjałów 1 V)

1 eV = 1,602·10-19 J

W przewodnikach (miedź, aluminium itp.) nie ma pasma zabronionego (przerwy energetycznej). Może to wynikać z dwóch powodów:

• Pasmo walencyjne jest tylko częściowo zapełnione elektronami, mogą się one swobodnie poruszać, a więc pasmo walencyjne w przewodnikach pełni analogiczną rolę jak pasmo przewodnictwa w półprzewodnikach i izolatorach.

• Pasmo przewodnictwa i walencyjne zachodzą na siebie, toteż w tym wspólnym paśmie występuje dużo elektronów swobodnych i możliwy jest przepływ prądu.

Różnica pomiędzy półprzewodnikiem a dielektrykiem jest umowna i dotyczy jedynie szerokości pasma zabronionego. Półprzewodniki mają pasmo zabronione o szerokości mniejszej bądź równej 2 eV (german 0,7 eV; krzem 1,1 eV), natomiast dielektryki -
o szerokości większej niż 2 eV.

4. Co jest mikroskopowym powodem występowania oporu elektrycznego?

Prawo Ohma o wzorze:

wyraża związek między różnicą potencjałów na końcach odcinka przewodnika, a natężeniem prądu płynącego przez przewodnik. Można jednak prawo Ohma zapisać w tzw. postaci mikroskopowej, która określa związek między natężeniem pola i gęstością prądu w danym punkcie przewodnika.

Rozpatrzymy ponownie przepływ prądu przez przewodnik o stałym przekroju poprzecznym

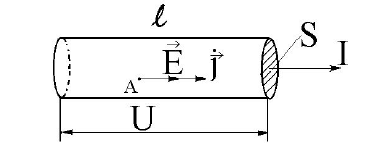
Jeśli oba końce przekroju przewodnika są powierzchniami ekwipotencjalnymi, natężenie pola E i gęstość prądu j będą miały stałą wartość i kierunek we wszystkich punktach rozpatrywanego przewodnika:

Korzystając z zależności oporu przewodnika o stałym przekroju poprzecznym:

oraz z przewodnictwa właściwego danego przewodnika

otrzymamy prawo Ohma w postaci:

skąd otrzymujemy wzór:

czyli, uwzględniając wzory na natężenie pola E i gęstość prądu j

Te ostatnie wzory przedstawiają prawo Ohma w postaci mikroskopowej. Należy podkreślić, ze wzór ten ma ogólniejszy charakter, niż prawo Ohma poznane wcześniej.

W tym przypadku widać, że opór jest zależny zarówno od natężenia pola jak i od gęstości prądu.

5. Dlaczego temperatura ma wpływ na wartość oporu elektrycznego? Jak zmienia się on dla metali, a jak dla półprzewodników (wzór i wykres)?

W zakresie temperatur pokojowych opór typowych przewodników jest stały. Przy większych zmianach temperatury opór rośnie proporcjonalnie do T. Jest to związane ze wzrostem liczby zderzeń elektronów z jonami sieci krystalicznej. W półprzewodnikach mechanizm ten jest słabszy w porównaniu z innym, który sprawia, że w materiałach tych opór maleje z temperaturą. Otóż ze wzrostem temperatury uwalniają się nowe elektrony (i dziury), wskutek czego liczba nośników prądu silnie rośnie, co przyczynia się do malenia oporu.

TABELA Z ĆWICZENIA:

TEMPERATURA		MIEDŹ		TERMISTOR
T [°C]	T [K]	[K]	y=R [Ω]		R [Ω]	y'= ln (R)
	297,15	0	1,09	0,003365303719	12,78	2,547881449
25	298,15	1	1,10	0,003354016435	12,14	2,496505786
30	303,15	6	1,11	0,003298697015	9,45	2,246014742
35	308,15	11	1,13	0,003245172805	6,67	1,897619860
40	313,15	16	1,15	0,003193357816	4,85	1,578978705
45	318,15	21	1,17	0,003143171460	3,88	1,355835154
50	323,15	26	1,21	0,003094538140	2,78	1,022450928
55	328,15	31	1,23	0,003047386866	2,13	0,756121979
60	333,15	36	1,26	0,003001650908	1,67	0,512823626
65	338,15	41	1,29	0,002957267485	1,24	0,215111379
70	343,15	46	1,33	0,002914177473	0,96	-0,040821994
75	348,15	51	1,36	0,002872325147	0,73	-0,314710744
80	353,15	56	1,40	0,002831579360	0,60	-0,510825624

Tabela pomocnicza do wykonania obliczeń dla regresji liniowej oporu Cu. (wykonana w Excelu)

n
1	0	1,09	0	1,19	0
2	1	1,10	1	1,21	1,1
3	6	1,11	36	1,23	6,66
4	11	1,13	121	1,28	12,43
5	16	1,15	256	1,32	18,40
	6	21	1,17	441	1,37	24,57
		7	26	1,21	676	1,46	31,46
		8	31	1,23	961	1,51	38,13
		9	36	1,26	1296	1,59	45,36
		10	41	1,29	681	1,66	52,89
		11	46	1,33	2116	1,77	61,18
		12	51	1,36	2601	1,85	69,36
		13	56	1,40	3136	1,96	78,40
Suma:	342	15,83	13322	19,41	439,94

Tabela pomocnicza do wykonania obliczeń do przerwy energetycznej (wykonana w Excelu)

n
1	0,003365303719	2,547881449	0,0000113253	6,491699878	0,008574395
2	0,003354016435	2,496505786	0,0000112494	6,23254114	0,008373321
3	0,003298697015	2,246014742	0,0000108814	5,044582221	0,007408922
4	0,003245172805	1,897619860	0,0000105311	3,600961133	0,006158104
5	0,003193357816	1,578978705	0,0000101975	2,493173751	0,005042244
6	0,003143171460	1,355835154	0,00000987953	1,838288965	0,004261622
7	0,003094538140	1,022450928	0,00000957617	1,0454059	0,003164013
8	0,003047386866	0,756121979	0,00000928657	0,571720447	0,002304196
9	0,003001650908	0,512823626	0,00000900911	0,262988071	0,001539318
10	0,002957267485	0,215111379	0,00000874543	0,046272905	0,000636142
11	0,002914177473	-0,040821994	0,00000849243	0,001666435	-0,000118963
12	0,002872325147	-0,314710744	0,00000825025	0,099042852	-0,000903952
13	0,002831579360	-0,510825624	0,00000801784	0,260942818	-0,001446443
Suma	0,036953341	11,2151038	0,000114118	21,49758664	0,036418526

Za pomocą regresji liniowej wyznaczę współczynnik temperaturowy oporu dla drutu miedzianego:

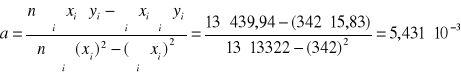
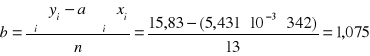
Wyznaczanie współczynnika

Temperatura tablicowa współczynnika oporu miedzi wynosi: α = 0,0043 Kˉ¹

Niepewność pomiarowa wyznaczenia współczynników a i b

=
=

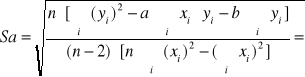
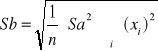
Wyznaczam za pomocą regresji liniowej stopień uzależnienia tych dwóch zmiennych:

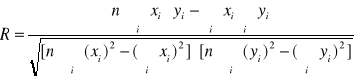
R oznacza, że stopień uzależnia od siebie dwie zmienne. Jeżeli wnosi jeden to dwie zmienne wprost proporcjonalnie zależne są od siebie. Z kolei, niepewność pomiarowa to błąd jaki mogłam uzyskać w czasie dokonywania pomiarów

Jak widać, wyniki są zbliżone do wartości tablicowych.

Za pomocą regresji liniowej wyznaczę szerokości przerwy energetycznej Eg termistora.

Wartość Eg=2*k*a

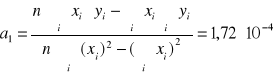
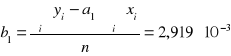
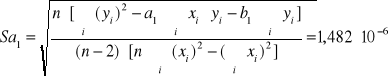
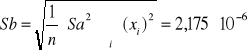
Wyznaczam za pomocą regresji liniowej stopień uzależnienia tych dwóch zmiennych:

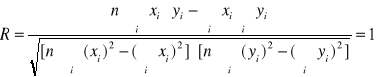
Jeśli R wyszło mi 1, oznacza to, że poprzednie wyniki zostały policzone prawidłowo.

Równanie prostej regresyjnej

eV

Wykres zależności oporu od temperatury dla miedzi:

w-równanie linii regresyjnej

Wykres zależności logarytmu naturalnego oporu od odwrotności temperatury bezwzględnej.*

* odwrotność temperatury bezwzględnej została zapisana w formie
, a miejsca po przecinku zostały zaokrąglone do dwóch dla bardziej precyzyjnego pokazania wyników.

Wnioski:

Teoria potwierdziła praktykę, że opór w przewodnikach rośnie razem z temperaturą, natomiast dla półprzewodników opór wykazuje cechy malejące.

Błędy którymi obarczone są wyniki otrzymane w ćwiczeniu zostały spowodowane przez dwie zasadnicze przyczyny :

- odczyt temperatury na skali termometru przy szybkich zmianach jej wartości był jedynie przybliżony co spowodowało niewielkie rozbieżności wyników (dla tej samej temperatury) otrzymanych przy ogrzewaniu rezystorów ,

- niedokładność multimetrów używanych do pomiaru rezystancji, która dała błąd dochodzący do 2% wartości mierzonej .

Charakterystyki wyznaczone podczas wykonywania ćwiczenia mają charakter liniowy, co pokrywa się wytycznymi teoretycznymi na ten temat. Również wartości temperaturowego współczynnika rezystancji
i szerokość pasma wzbronionego półprzewodnika Eg = 9,369∙10

eV pokrywają się z wartościami podawanymi w tablicach .

Zjawisko zmiany wartości rezystancji pod wpływem zmian temperatury znalazło szerokie zastosowanie w technice. Często stosowane są termometry oporowe platynowe pozwalające mierzyć temperatury w zakresie od -200 do +550C . Pomiar tą metodą może być bardzo dokładny po zastosowaniu odpowiednio wysokiej klasy miernika rezystancji wyskalowanego w jednostkach temperatury.

Termistor jest to element półprzewodnikowy, którego rezystancja silnie zależy od temperatury. W ćwiczeniu wykorzystany był element, którego rezystancja rośnie wykładniczo wraz ze wzrostem temperatury. Istnieją także termistory, których rezystancja maleje ze wzrostem temperatury, jak i takie o nagłym skokowym zmniejszeniu się rezystancji w wąskim przedziale temperatury. Termistory zasadniczo wytwarzane są z tlenków manganu, tytanu, niklu, kobaltu, żelaza, glinu , miedzi i litu. Ich sproszkowane mieszaniny prasuje się a następnie spieka lub stapia w celu otrzymania elementów o wymaganych kształtach i rozmiarach. Termistory stosuje się przede wszystkim w termometrii jako wysokoczułe czujniki temperatury, a ponadto w układach kompensacji temperaturowej układów elektronicznych i do pomiaru mocy prądu wysokich częstotliwości .

---