WYKŁAD 4 - POCHODNA FUNKCJI

PROBLEM I

Obliczyć kąt nachylenia do osi OX stycznej do krzywej
w punkcie P=(2,4)

y y = x²

⁴ P = (2, 4)

₂ x

Do wyznaczenia linii, która będzie styczna do paraboli potrzebujemy 2 punkty. Wiemy tylko, że przechodzi ona przez punkt o współrzędnych (2,4).

• Znajdujemy dowolny punkt Q na krzywej, np.: Q=(2.1,2.1²)

• Prowadzimy sieczną do wykresu funkcji przechodzącą przez punkty P i Q

• Znajdujemy tangens kąta jaki tworzy sieczna wykresu funkcji z osią OX

Y y = x² Q = (2.1, 2.1²)

Q = (2.1, 2.1²)

⁴ P = (2, 4)

P = (2, 4)

₂ x

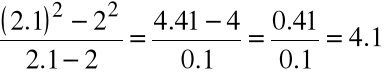
• Otrzymaną wartość traktujemy jako przybliżoną wartość tangensa kąta nachylenia stycznej do krzywej do osi OX w punkcie P=(2,4).

• W celu otrzymania lepszego przybliżenia tej wartości powtarzamy w/w procedurę wykorzystując sieczną między punktami P=(2,4) i Q=(2.01,2.01²)

• Ogólnie, rozważamy linię poprowadzoną przez punkty: P=(2,4) i Q=(2+h,(2+h)²), gdzie h jest małą wartością dodatnią lub ujemną

Tangens kąta nachylenia stycznej do krzywej do osi OX, wyraża się wtedy wzorem:

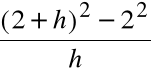
W celu określenia jak zmienia się ta wartość w przypadku gdy h dąży do 0, liczymy granicę tego wyrażenia:

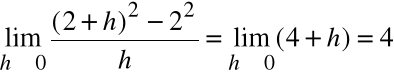
Stąd, tangens kąta nachylenia stycznej do osi OX wynosi 4

Y y = x²

Q = [2+h, (2+h)²]

(2.2, 4.84)

P = (2, 4)

(2.1, 4.41)

(2, 4)

_{2 (2+h)} x

• POCHODNA FUNKCJI

- funkcja
- ustalony punkt

• 
  - przyrost zmiennej niezależnej x,

lub
,

;

• 
  - przyrost wartości funkcji odpowiadający

przyrostowi
:

,

>0,
<0 lub
=0

Zamiast
piszemy także
.

Definicja

Ilorazem różnicowym funkcji
w punkcie
,

dla przyrostu
zmiennej niezależnej nazywamy iloraz:

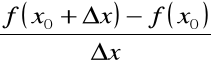
y f(x)

f(

0

Interpretacja geometryczna ilorazu różnicowego

w prostokątnym kartezjańskim układzie współrzędnych

y

y=f(x) sieczna

styczna

0

x

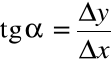
= tangens kąta nachylenia siecznej

Przykład

Iloraz różnicowy funkcji
w punkcie

dla przyrostu
wynosi

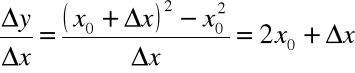
Interpretacja fizyczna ilorazu różnicowego

Przykład 1

Punkt P porusza się po osi liczbowej OS.

Współrzędna s punktu P jest funkcją czasu
.

0 s
s

s

Iloraz różnicowy przedstawia prędkość średnią tego ruchu między chwilą
i chwilą

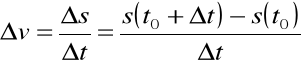
Dla
:

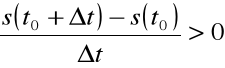
Punkt P przemieści się od chwili
do chwili

w dodatnim kierunku OS.

Przykład 2

Przez przewodnik (np. drut) płynie prąd elektryczny. Ustalamy umownie dodatni kierunek prądu, który zaznaczamy na rysunku strzałką.

Ładunek elektryczny q, jaki przepłynął w tym dodatnim kierunku przez poprzeczny przekrój przewodnika

w czasie
.

Iloraz różnicowy przedstawia

średnie natężenie prądu

między chwilą
i chwilą
.

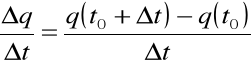
0

Q

Niech
, wtedy

• 
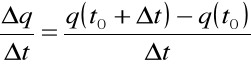
  >0, dla
  

Ładunek q doznał od chwili
do chwili
dodatniego przyrostu
.

W rozpatrywanym przedziale czasu
, wypadkowy ładunek, który przepłynął, jest taki,

jak w przypadku prądu stałego o natężeniu
,

a więc o kierunku rzeczywistym zgodnym z umownie przyjętym dodatnim kierunkiem prądu.

• 
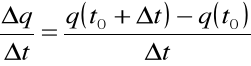
  <0, dla
  

Ładunek doznał ujemnego przyrostu
.

Ujemna wartość ilorazu różnicowego oznacza,

że wypadkowy ładunek, który przepłynął w przedziale czasu
, jest taki, jak w przypadku prądu stałego o natężeniu
, więc o kierunku rzeczywistym przeciwnym do umowie przyjętego dodatniego kierunku prądu.

Definicja

Granicę właściwą ilorazu różnicowego

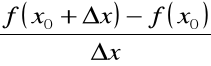
, gdy
,

nazywamy pochodną funkcji
w punkcie

i oznaczamy symbolem
.

Jeżeli istnieje powyższa granica to mówimy, że pochodna funkcji w punkcie istnieje (funkcja jest różniczkowalna w )

Jeżeli nie istnieje powyższa granica to mówimy, że pochodna funkcji w punkcie nie istnieje (funkcja nie jest różniczkowalna w )

Przykład

a) Funkcja
ma pochodna równą

w dowolnym punkcie
, ponieważ:

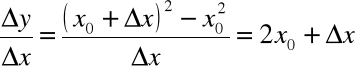
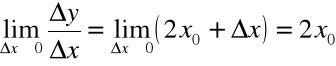
b) Funkcja stała f(x)=c ma pochodną równa 0 (zawsze !)

Interpretacja geometryczna pochodnej funkcji

w prostokątnym kartezjańskim układzie

współrzędnych

y

y=f(x) sieczna

styczna

0

x

Jeżeli
, to geometrycznym odpowiednikiem istnienia granicy

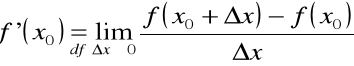
jest istnienie granicznego położenia siecznej do wykresu funkcji
, czyli istnienie stycznej do tego wykresu w punkcie (
,
).

= tangens nachylenia stycznej

Interpretacja fizyczna pochodnej funkcji

Granicę właściwą ilorazu różnicowego

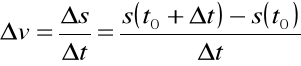
, gdy
,

nazywamy prędkością v punktu P w chwili

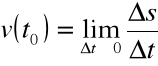
Granicę właściwą ilorazu

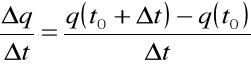
, gdy
,

nazywamy natężeniem prądu i w chwili

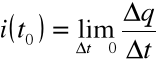
Liczba
- prędkość przepływu ładunku elektrycznego w chwili
.

Jeżeli
, to znaczy, że prąd w chwili
płynie

w kierunku przeciwnym do przyjętego umownie za dodatni.

Przykład

Obliczyć pochodną funkcji
w punktach -3, 0, 5.

,
.

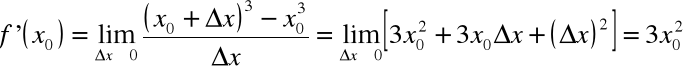
Definicja

Jeżeli pochodna funkcji istnieje w każdym punkcie pewnego zbioru X, to każdej liczbie przyporządkowana jest dokładnie jedna liczba , a więc w zbiorze X określona jest nowa funkcja, zwana funkcją pochodną funkcji i oznaczana .

Przykład

Funkcja
posiada funkcję pochodną
, określoną w zbiorze R.

Należy oczywiście rozróżniać funkcję pochodną

oraz pochodną w pewnym ustalonym punkcie,

która jest liczbą równą wartości funkcji pochodnej w tym punkcie.

Jeżeli piszemy
, to zamiast
piszemy też
, zamiast zaś
możemy pisać
.

Pochodne funkcji podstawowych

	Funkcja	Pochodna	Uwagi
1			c჎R
2
3
4
5
6

• Notacja Leibniza

Jeżeli mamy funkcję którą oznaczymy jako

to funkcję
oznacza się czasami jako

a jej wartość w punkcie
jako

Wielkość nazywamy różniczką funkcji f(x) dla przyrostu argumentu dx. Oznacza ona liniową część przyrostu funkcji dla przyrostu argumentu dx w punkcie

Przykład

Jeżeli
to wówczas:

,

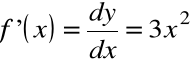
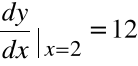
Przykład

,
,

Definicja

Pochodną lewostronną funkcji
w punkcie
, którą oznaczamy symbolem
, oraz

pochodną prawostronną funkcji
w punkcie
,

którą oznaczamy symbolem
nazywamy, odpowiednio granice jednostronne:

,

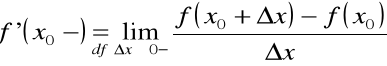
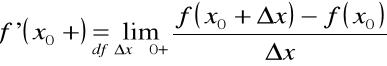
Twierdzenie

Jeżeli istnieje pochodna , to istnieją pochodne jednostronne i wszystkie trzy są równe. Jeżeli istnieją pochodne jednostronne i są równe, to istnieje pochodna i jest im równa. Samo istnienie pochodnych jednostronnych nie zapewnia jednak istnienia pochodnej .

Zanotujmy też związek różniczkowalności z ciągłością.

Twierdzenie

Jeżeli istnieje pochodna to funkcja jest ciągła w . Jeśli pochodna istnieje dla wszystkich argumentów f to funkcja f(x) jest ciągła w swojej dziedzinie

Przykład

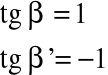
β' β

Funkcja
posiada w punkcie
pochodne jednostronne:

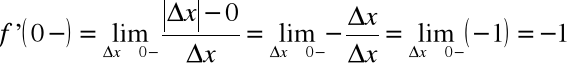
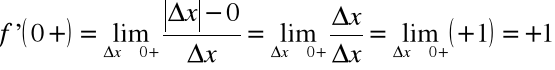
Pochodne jednostronne funkcji f(x) w punkcie

są różne, a zatem
nie istnieje.

Definicja

Jeżeli funkcja : posiada pochodną w przedziale , istnieją pochodne jednostronne i , to mówimy, że istnieje pochodna w przedziale domkniętym .

Arytmetyka pochodnych ma swoją specyfikę w porównaniu z arytmetyką granic funkcji

Twierdzenie - arytmetyka pochodnych

Jeżeli f(x) i g(x) są różniczkowalne w x, to wówczas:

(1)

(2)

(3)

(4)

Dowód (pochodna iloczynu)

.

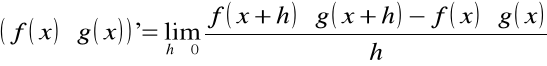
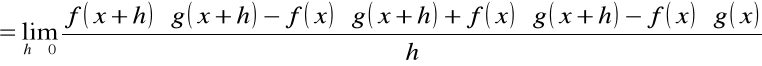
Dowód (pochodna ilorazu)

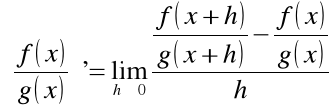
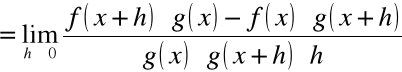
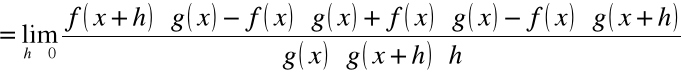
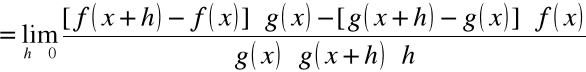
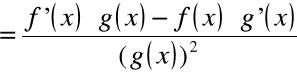
W notacji Leibnitza:

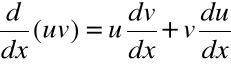
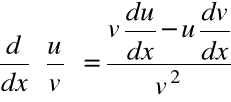
gdzie u i v są różniczkowalnymi funkcjami x

Wniosek (różniczkowanie funkcji potęgowej)

Jeśli
dla pewnego
to

Wniosek

	Funkcja	Pochodna	Uwagi
1
2
3

Przykłady

,

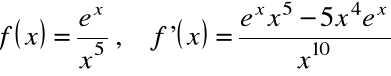
Twierdzenie (o pochodnej funkcji odwrotnej)

Jeżeli funkcja : jest ściśle monotoniczna, posiada funkcję pochodną to funkcja odwrotna do niej posiada funkcję pochodną , przy czym , gdzie dla każdego x z dziedziny funkcji f(x)

Dowód

Wobec przyjętych oznaczeń mamy:
,

funkcja f ściśle monotoniczna i ciągła

funkcja g ściśle monotoniczna i ciągła.

Stąd
, gdy
i
, gdy
.

Ponadto:

Mamy więc

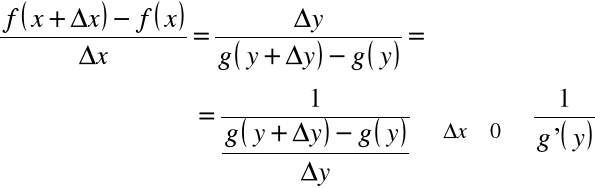
Interpretacja geometryczna twierdzenia w przypadku funkcji rosnącej

Y
y=g(x)

y=x

y=f(x)

0

X

,
,

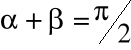
, dla funkcji malejących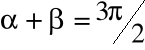
,

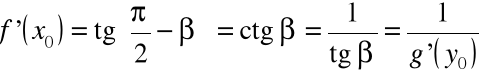
Wzór można zapisać krótko posługując się symbolem funkcji odwrotnej

albo posługując się różniczkami: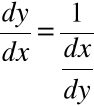
.

Przykład

	Funkcja	Pochodna	Uwagi
1
2
3
4
5
6
7

1) Dla
,

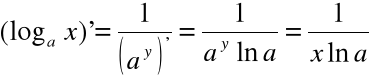
2) Wzór jest szczególnym przypadkiem poprzedniego

3) Mamy tu
,

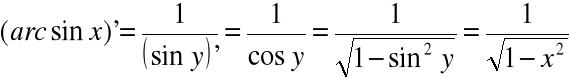
Uwaga:

Z dwóch możliwości:

;

wybraliśmy drugą dlatego, że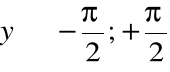
,

a wówczas
.

4)
,

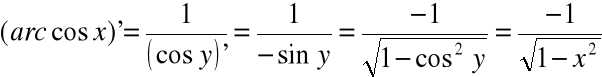
5)
,
, więc

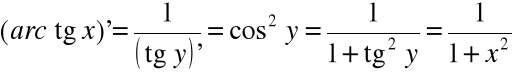
6)
,

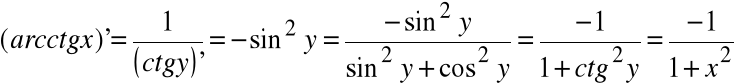
Twierdzenie (o pochodnej funkcji złożonej, reguła łańcuchowa)

Jeżeli: funkcja f ma pochodną w punkcie x, funkcja g ma pochodną w punkcie to wówczas: funkcja złożona ma w punkcie x pochodną

Pochodna funkcji złożonej jest iloczynem pochodnej funkcji zewnętrznej i pochodnej funkcji wewnętrznej

W notacji Leibniza:

Jeśli y jest różniczkowalną funkcją u, (tzn. y=y(u))

i u jest różniczkowalną funkcją x, (tzn. u=u(x)),

to wówczas:

Wniosek

,

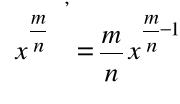
ogólnie można udowodnić, że

Przykłady

1. 
   ;
   ,
   ,

,

2. 
   ;
   ,
   ,

,

3. 
   ;
   ,
   ,

,

4. 
   ;
   ,
   ,

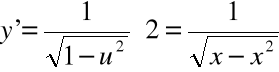
e)
;
,

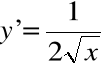
f)
;
,

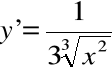
g)
;
,
,

,

8. 
   ;

,

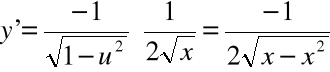
i)
;

,

j)
;
,

,

k)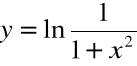
;

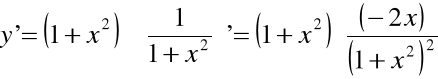
Pochodna logarytmiczna

Rozważmy sczególną postać funkcji f(x):

Żeby znaleźć pochodna takiej funkcji należy zastosować tożsamość algebraiczną:

wynikającą z faktu że złożenie funkcji wykładniczej i funkcji logarytmicznej odwrotnej do niej daje nam przekształcenie tożsamościowe.

Teraz dopiero możemy różniczkować tę postać stosując wzór na pochodną funkcji złożonej.

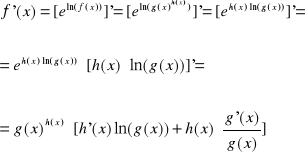
Przykład

Obliczyc pochodną funkcji:

A zatem pochodna:

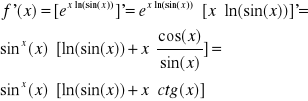
PJWSTK

Analiza Matematyczna 1

20

•

•

•

•

•

•

•

•

•

•