Momenty centralne

Przykład 1

Centralny moment trzeciego rzędu:

1. na podstawie szeregu szczegółowego:

= 19,167,

μ₃ =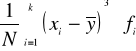
=

=
[(7-19,167)³⋅1 + (11-19,167)³⋅3 + (16-19,167)³⋅4 + (17-19,167)³⋅7 +

+ (18-19,167)³⋅9 + (22-19,167)³⋅6 + (26-19,167)³⋅3 + (31-19,167)³⋅1 +

+ (32-19,167)³⋅2] =
= 92,51.

2. na podstawie rozkładu przedziałowego.

= 18,1,

μ*₃ =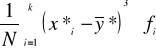
=
[(9,5-18,1)³⋅4 + (14,5-18,1)³⋅11 +

+ (19,5-18,1)³⋅15 + (24,5-18,1)³⋅3 + (29,5-18,1)³⋅3] =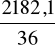
= 60,61.

Przykład 2

Centralny moment czwartego rzędu:

1. na podstawie szeregu szczegółowego: (
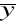
   = 19,167)

μ₄ =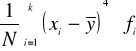
=

=
[(7-19,167)⁴⋅1 + (11-19,167)⁴⋅3 + (16-19,167)⁴⋅4 + (17-19,167)⁴⋅7 +

+ (18-19,167)⁴⋅9 + (22-19,167)⁴⋅6 + (26-19,167)⁴⋅3 + (31-19,167)⁴⋅1 +

+ (32-19,167)⁴⋅2] =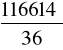
= 3239,3.

2. na podstawie rozkładu przedziałowego.

= 18,1,

μ*₃ =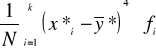
=
[(9,5-18,1)⁴⋅4 + (14,5-18,1)⁴⋅11 +

+ (19,5-18,1)⁴⋅15 + (24,5-18,1)⁴⋅3 + (29,5-18,1)⁴⋅3] =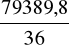
= 2205,3.

Miary asymetrii

Przykład 1

Współczynnik asymetrii As₁

1. na podstawie szeregu szczegółowego;

=
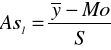
= 0,212.

2. na podstawie rozkładu przedziałowego.

=
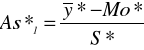
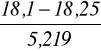
= -0,027.

Przykład 2

Współczynnik asymetrii As₂

1. na podstawie szeregu szczegółowego;

μ₃ = 92,51, S = 5,505,

=
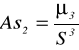
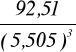
= 0,55.

2. na podstawie rozkładu przedziałowego.

μ*₃ = 60,61, S = 5,219,

=
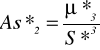
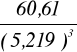
= 0,426.

Przykład 3

Współczynnik asymetrii As₃

1. na podstawie szeregu szczegółowego;

Me = 18, Q₁ = 17, Q₃ = 22,

=
=

=
=
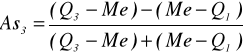
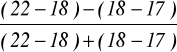
= 0,6.

2. na podstawie rozkładu przedziałowego.

Me* = 18, Q*₁ = 14,27, Q*₃ = 22,8,

=
=

=
=
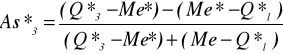
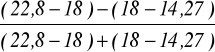
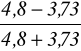
= 0,126.

1

---