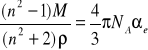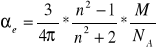I. WSTĘP TEORETYCZNY

Każda cząsteczka dielektryka zawiera jądra naładowane dodatnio oraz elektrony poruszające się wokół tych jąder. Zastępując wszystkie ładunki dodatnie jąder cząsteczki ładunkiem +q (znajdującym się w środku ciężkości ładunków składowych), a wszystkie ładunki ujemne ładunkiem wypadkowym -q, położonym w ich środku ciężkości, cząsteczkę dielektryka rozpatrywać można jako dipol złożony z ładunków +q, -q.

W przypadku wprowadzenia dielektryka w obręb pola elektrycznego, następuje tzw. polaryzacja dielektryka. Aby zaobserwować zjawisko polaryzacji dielektryka należy wprowadzić go w obszar pola elektrycznego (np. pomiędzy okładki naładowanego kondensatora). W ogólnym przypadku mogą wtedy zachodzić trzy zjawiska:

Jeżeli cząsteczka jest dipolem elektrycznym wówczas na jej biegun dodatni działa siła „kolumbowska” skierowana wzdłuż przechodzących przez ten punkt linii sił pola elektrycznego w kierunku zgodnym z nimi, na biegun ujemny zaś siła o zwrocie przeciwnym. Ta para sił stara się ustawić tę cząsteczkę tak, aby jej oś była położona wzdłuż linii sił pola elektrycznego i charakteryzowała się minimalną energią potencjalną. Zjawisko to nazywamy polaryzacją skierowaną.

W polu elektrycznym na dodatnie jądra atomowe działają siły przesuwające je wzdłuż linii sił pola elektrycznego zgodnie z ich zwrotem, natomiast elektrony w stronę przeciwną. Ze względu na małą masę przesunięciu ulegają głównie elektrony powodując deformację powłok elektronowych. Zjawisko to nazywamy polaryzacją elektronową. Po zaniku działania pola elektrycznego deformacja znika i cząsteczki tracą swoją biegunowość.

Atomy lub grupy polarne cząsteczki pod wpływem zewnętrznego pola elektrycznego ulegają przesunięciu lub obrotowi. Zjawisko to nazywamy polaryzacją jonową.

Zjawisko polaryzacji jest sumą trzech omówionych procesów, przy czym zjawisko drugie i trzecie występuje w cząsteczkach wszystkich substancji, a pierwsze tylko

w substancjach polarnych.

W ten sposób całkowita polaryzowalność substancji (a) jest sumą trzech polaryzowalności: skierowanej (a_sk), jonowej (a_j), elektronowej (a_e).

a = a_sk + a_j + a_e

Celem ćwiczenia jest zbadanie zależności współczynnika załamania wody od temperatury i wyznaczenie polaryzowalności elektronowej wody.

Aby wyznaczyć polaryzowalność elektronową wody trzeba zastosować zmienne pole elektryczne i wykorzystać różnice pomiędzy różnymi rodzajami polaryzacji. Cząsteczki wody należy umieścić w polu elektrycznym o optycznej częstotliwości (10¹⁴-10¹⁵Hz). A więc należy oświetlić je widzialną falą elektromagnetyczną, gdyż ona zawiera w sobie wymagane pole elektryczne. Jeśli ośrodek nie jest ferromagnetyczny jego współczynnik załamania (n) jest wyrażony wzorem n=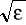
(z teorii Maxwella), skąd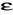
=n².

Równanie Clausiusa - Mosottiego określa zależność polaryzowalności substancji

z jej stałą dielektryczną (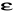
):

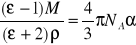
/1/

gdzie : M - masa cząsteczkowa substancji,

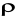
- gęstość substancji,

N_A- liczba Avogadra.

Stosując to równanie tylko dla polaryzowalności elektronowej i uwzględniając, że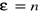
²

Otrzymuję wzór Lorentza:

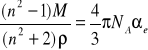
/2/

Dokonując pomiaru współczynnika załamania wody dla światła widzialnego można wyznaczyć jej polaryzowalność elektronową.

Z przekształcenia wzoru Lorentza:

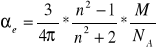
/3/

Z teorii wynika, że polaryzowalność elektronowa cząsteczki równa się w przybliżeniu sześcianowi jej promienia.

Wyznaczanie współczynnika załamania światła jakiegoś ciała polega na zmierzeniu wartości kąta granicznego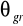
. Na tej zasadzie są zbudowane przyrządy do mierzenia współczynników załamania światła dla cieczy i ciał stałych, tzw. refraktometry. W swoim doświadczeniu wykorzystałem refraktometr Abbego.

2. Obliczenie polaryzowalności wody dla wybranych wartości temperatury:

a) podczas ogrzewania:

/4/

gdzie, n1- wartość temp. podczas ogrzewania

Tabela 2: Zestawienie obliczeń polaryzowalności elektronowej podczas podgrzewania wody

Temperatura [C]	Wartości polaryzowalności elektronowej [m^3]
21	0,1472 *10^-23
25	0,1473 *10^-23
30	0,1474 *10^-23
35	0,1476 *10^-23
40	0,1464 *10^-23
45	0,1464 *10^-23
50	0,1461 *10^-23

b) podczas schładzania:

/5/

gdzie, n2- wartość temp. podczas schładzania

Tabela 3: Zestawienie obliczeń polaryzowalności elektronowej podczas schładzania wody

Temperatura [C]	Wartości polaryzowalności elektronowej [m^3]
50	0,1461 *10^-23
45	0,1461 *10^-23
40	0,1463 *10^-23
35	0,1465 *10^-23
30	0,1474 *10^-23
25	0,1469*10^-23
21	0,1472*10^-23

c) średnia wartość podczas ogrzewania oraz schładzania:

/6/

gdzie, n_a -średnia wartość temp.

Tabela 4: Zestawienie średnich wartości polaryzowalności

Temperatura [C]	Średnie wartości polaryzowalności elektronowej [m^3]
21	0,1472 *10^-23
25	0,1471 *10^-23
30	0,1474 *10^-23
35	0,1466 *10^-23
40	0,1464 *10^-23
45	0,1462 *10^-23
50	0,1461 *10^-23

3. Oszacowanie granicznego błędu wyznaczenia gęstości wody (δς) :

/7/

gdzie, ς_{i -} gęstość wody w danej temp.

T_{i -} dana wartość temp.

Do danych temperatur oraz przypisanych do nich gęstości wody zastosowaliśmy wzór /7/. Maksymalna wartość stanowi błąd graniczny.

δς= 0,0436 * kg.*m^-3

4. Obliczenie względnego błędu granicznego polaryzowalności _a dla wybranej temperatury:

/8/

gdzie, δn_a - gęstość średniej wartości temp.

Względny błąd graniczny polaryzowalności dla temperatur wynosi

_{a = 0,00032}

5. Obliczenie bezwzględnego błędu granicznego (Δ_a) :

/9/

Tabela 5: Zestawienie wartości bezwzględnego błędu granicznego

Temperatura [C]	Bezwzględny błąd graniczny [m^3]
21	0.00046
25	0.00046
30	0.00046
35	0.00046
40	0.00046
45	0.00046
50	0.00047

IV. OMÓWIENIE WYNIKÓW ĆWICZENIA

Przeprowadzone przeze nas doświadczenie jest praktycznym dowodem na to, że współczynnik załamania światła jest zależny niemalże liniowo od temperatury. Wyniki pomiarów wykazały to w dostatecznym stopniu.

Doświadczenie wykazało także, iż polaryzowalność elektronowa wody praktycznie nie zależy od temperatury. Różnica wyników mieści się w granicy błędu. Jest tak, ponieważ dipole zwane indukowanymi (istniejące tylko

w zewnętrznym polu) ustawiają się zawsze zgodnie z liniami sił pola elektrycznego niezależnie od ruchu cieplnego i związanej z nią temperatury.

Ćwiczenie potwierdziło także wyeliminowanie wpływu polaryzacji skierowanej

i jonowej poprzez odpowiedni dobór częstotliwości pola zewnętrznego (widzialne fale elektromagnetyczne). Wynika to z tego, że wyniki pomiarów z dość dobrym przybliżeniem nie zależą od temperatury, a zależałyby gdyby na wyniki miały wpływ polaryzacje skierowana i jonowa, które zależą od ruchów cieplnych.

Ogólnie dokładność pomiarów oceniamy na dość dobrą, a błędy w wyznaczeniu elektronowej polaryzowalności wody spowodowane są nałożeniem się błędów odczytu temperatury Dt=0.1oC, błędu odczytu współczynnika załamania Dn=0.0001 a także gęstości wody.

---