Dr inż. Janusz Sowiński

Instytut Elektroenergetyki

Politechnika Częstochowska

Materiały pomocnicze do zajęć z przedmiotu „Gospodarka elektroenergetyczna”

Opracowano na podstawie: Sowiński J., Inwestowanie w źródła wytwarzania energii elektrycznej w warunkach rynkowych, Wydawnictwa Politechniki Częstochowskiej, Częstochowa 2008, ISBN 978-83-7193-398-1

4. Podejmowanie decyzji o inwestowaniu w warunkach ryzyka

4.1. Klasyczne metody oceny konkurencyjności technologii wytwarzania energii elektrycznej

4.1.1. Metoda UNIPEDE

Powszechnie stosowaną metodą oceny pod względem ekonomicznym różnych rodzajów technologii wytwarzania energii elektrycznej wg [69] jest metodyka opracowana pod koniec lat 70. przez UNIPEDE, a następnie wykorzystywana w krajach Unii Europejskiej. Metoda wykorzystuje zdyskontowany jednostkowy koszt wytwarzania, określony jako stosunek całkowitych kosztów budowy i eksploatacji elektrowni w okresie jej „życia” do zdyskontowanej ilości energii elektrycznej wyprodukowanej w adekwatnym okresie. W [69] podano sposób wyznaczania jednostkowego kosztu wytwarzania:

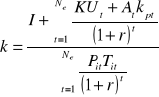
(4.1)

gdzie:

I - zdyskontowany nakład inwestycyjny,

N_e - czas życia elektrowni,

- koszty utrzymania i remontów w roku t,

- energia elektryczna wytworzona w roku t,
,

- koszt paliwa na wytworzenie jednostki energii elektrycznej w roku t,

r - stopa dyskonta,

- moc zainstalowana elektrowni w roku t,

- czas wykorzystania mocy zainstalowanej w roku t.

Natomiast dla projektowanych obiektów podano w [69] wzór na długookresowy jednostkowy koszt produkcji w elektrowniach w postaci:

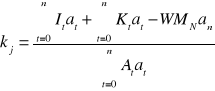
(4.2)

gdzie:

,
- współczynniki dyskontowe,
,
,

n - okres analizy, obejmujący budowę i okres eksploatacji elektrowni,

- nakłady inwestycyjne w roku t,

- bieżące koszty eksploatacji obiektu w roku t,

- wartość niezamortyzowana majątku trwałego w ostatnim roku eksploatacji,

Jednostkowy koszt produkcji energii porównuje się z wartością średniej zdyskontowanej ceny energii elektrycznej, wyznaczanej ze wzoru:

(4.3)

gdzie:

- stopa amortyzacji oprocentowanej (stopa zwrotu kapitału wraz z odsetkami od niego),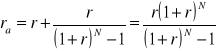
,

- prognozowana cena energii elektrycznej w roku t.

Kryterium opłacalności produkcji energii elektrycznej określa wzór:

lub
(4.4)

gdzie:

z - założony minimalny zysk brutto.

Najbardziej efektywną technologią jest ta, która daje minimalną wartość jednostkowego kosztu produkcji energii elektrycznej.

4.1.2. Podejście klasyczne do inwestowania

Podstawowym celem rachunku efektywności inwestycji jest ocena pojedynczego projektu przedsięwzięcia gospodarczego lub wyłonienie, spośród wielu możliwych do realizacji wariantów, najbardziej opłacalnego przedsięwzięcia [37-39, 57, 58]. Obecnie coraz popularniejsze stają się rynkowe, dynamiczne metody oceny efektywności inwestowania, w których rachunek inwestycyjny opiera się na przychodach i nakładach. Metody te pozwalają analizować inwestycje w warunkach ryzyka i niepewności dotyczącej kształtowania się cen i kosztów [10, 37, 40, 46].

W propagowanych oraz stosowanych przez Bank Światowy i UNIDO metodach oceny efektywności projektów inwestycyjnych [17] (np. Computer Model for Feasibility Analysis and Reporting COMFAR III Expert) powszechnie uznaje się, że najwłaściwszym kryterium jest zysk, który powinien uwzględniać ryzyko i niepewność w warunkach konkurencyjnych, oraz czas, wiążący się z rozłożeniem w kolejnych latach ponoszonych nakładów i uzyskiwanych przychodów z przedsięwzięcia inwestycyjnego.

Wśród prostych metod oceny efektywności wg [17] wyróżniamy okres zwrotu nakładów, prostą stopę zwrotu (zysku) oraz tzw. test pierwszego roku.

Analiza rentowności przedsiębiorstwa bazuje na miernikach prorynkowych, takich jak stopa zysku ROI (Return on Investment), to stosunek zysku operacyjnego do zainwestowanego majątku, oraz stopa zwrotu kapitału ROE (Return of Equity), definiowana jako stosunek zysku netto do kapitału netto. Przy porównywaniu wariantów najlepszy jest ten, który wykazuje większą wartość ROI i ROE.

W analizach w elektroenergetyce [2, 4, 37, 56, 78, 83, 85, 97] wykorzystuje się wiele mierników efektu ekonomicznego inwestycji, m.in. wartość zaktualizowaną netto (NPV - Net Present Value), wewnętrzną stopę zwrotu (IRR - Internal Rate of Return), próg rentowności (BEP - Break Even Point), prosty i zdyskontowany okres zwrotu nakładów inwestycyjnych (SPB i DPB - Simple and Discounted Pay Back). Przegląd standardowych metod oceny efektywności przedsięwzięć gospodarczych w energetyce dokonany został m.in. w [36].

Do metod dynamicznych, w których uwzględniany jest rachunek dyskonta i które są stosowane w energetyce [37], należą:

• metoda równoważnego (jednostkowego) kosztu rocznego (EAW - Equivalent Annual Worth)

• metoda zaktualizowanej wartości netto (tzw. metoda NPV - Net Present Value)

• metoda wewnętrznej stopy zwrotu (tzw. metoda IRR - Internal Rate of Return)

• metoda zmodyfikowanej stopy zwrotu (tzw. metoda MIRR - Modified Internal Rate of Return)

• metoda wskaźników rentowności (tzw. metoda PI - Profitability Index).

Wskaźnik NPV w sposób dogodny umożliwia uwzględnienie niepewności inwestowania, a jednocześnie w układzie wielookresowym metoda wartości zaktualizowanej netto jest zawsze zgodna z ogólnym celem finansowym firmy, czyli postulatem maksymalizacji majątku, podczas gdy np. wewnętrzna stopa zwrotu jest jedynie względnym miernikiem majątku

Wskaźnik NPV (w przypadku pominięcia wartości likwidacyjnej przedsięwzięcia inwestycyjnego) równy jest zdyskontowanym przepływom gotówkowym pomniejszonym o koszt inwestycji I (zdyskontowany na chwilę rozpoczęcia eksploatacji). W postaci dyskretnej:

(4.5)

gdzie:

r - stopa dyskonta przyjęta przez inwestora,

- przepływy pieniężne (ang. Cash Flow) w kolejnych latach t, będące różnicą między faktycznymi wpływami i wydatkami.

Przepływy pieniężne
, które są dla inwestora osiągniętym w danym roku efektem finansowym i które w przybliżeniu są równe rocznemu zyskowi po opodatkowaniu i amortyzacji [69] (zwane również rocznym zyskiem operacyjnym [5]), można wyznaczyć na podstawie wzoru:

(4.6)

gdzie:

- wpływy w danym roku t ze sprzedaży produktów (energii elektrycznej, ciepła, usług systemowych itp.),

- wydatki w danym roku t.

Na przewidywane wydatki w danym roku
składają się: koszty surowców (paliwa) i energii, koszty płac, koszty opłat za eksploatację środowiska, koszty remontów, koszty sprzedaży, ubezpieczenia i pozostałe koszty (np. obsługa finansowa kredytów, podatek dochodowy od zysku brutto) w danym roku.

Nakłady inwestycyjne poniesione w okresie N_b trwania budowy, zdyskontowane na chwilę rozpoczęcia jej eksploatacji, wyrażają się wzorem:

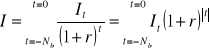
(4.7)

We wzorze (4.7) ostatnia część nakładów
jest niedyskontowana, jako że dyskontujący ją czynnik przyjmuje wartość równą 1.

Przyjmując zwykłe kryterium planowania inwestycji, inwestycję należy zrealizować, jeśli wartość zaktualizowana netto inwestycji, czyli wskaźnik NPV jest dodatni.

W przypadku uwzględniania ciągłego charakteru przepływów pieniężnych (założenie to przyjęto w dalszej części pracy) wzór na wartość zdyskontowaną netto przyjmuje postać:

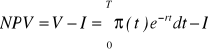
(4.8)

Próg rentowności BEP to taka wielkość produkcji przedsiębiorstwa, przy której przychód uzyskany ze sprzedaży wyrobów jest równy kosztom poniesionym na ich wytworzenie. Wynik finansowy dla progu rentowności wynosi zero, dopiero zwiększenie sprzedaży będzie powiększało poziom zysku, natomiast zmniejszenie - straty. Próg rentowności może być wyznaczany jako próg ilościowy lub wartościowy. Może on ponadto informować, jaką część zdolności produkcyjnej (lub przewidywanego popytu) trzeba wykorzystać, aby ponoszone koszty zrównoważyć przychodami ze sprzedaży.

W klasycznej metodzie wyznaczania progu rentowności przyjmuje się następujące założenia upraszczające:

• wielkość produkcji wytworzonej w badanym okresie jest równa ilości produkcji sprzedanej,

• koszty produkcji są funkcją wielkości produkcji,

• koszty stałe produkcji są jednakowe dla każdej wielkości produkcji,

• całkowite koszty zmienne są proporcjonalne do rozmiarów produkcji, a jednostkowe koszty zmienne kształtują się na tym samym poziomie,

• jednostkowa cena sprzedaży poszczególnych wyrobów nie zmienia się w czasie lub wraz ze zmianą skali produkcji w badanym okresie,

• poziom jednostkowych kosztów zmiennych i stałych kosztów produkcji nie zmienia się w całym badanym okresie.

Ilościowy próg rentowności jest to wielkość produkcji wyrobu wyrażona w jednostkach naturalnych, którą należy zrealizować przy założonym poziomie kosztów i ceny, aby przychód ze sprzedaży wyrobu pokrywał koszty poniesione na jego wytworzenie. Ilościowy próg rentowności produkcji jednoasortymentowej wylicza się ze wzoru:

(4.9)

gdzie:

- koszty stałe produkcji,

- cena,

- jednostkowy koszt zmienny.

Wartościowy próg rentowności to wielkość przychodu ze sprzedaży wyrobów, która zapewnia pokrycie kosztów poniesionych na ich wytworzenie (stałych i zmiennych), przy założonej wysokości kosztów i ceny. Wartościowy próg rentowności dla produkcji jednoasortymentowej określa się wzorem:

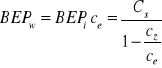
(4.10)

Metoda wyznaczania progu rentowności zakłada statyczny charakter ceny i kosztów. Wad tych nie posiada metoda oparta na wskaźniku NPV.

4.2. Ekonomiczna efektywność technologii wytwarzania energii elektrycznej w warunkach niepewności i ryzyka

4.2.1. Terminologia wykorzystywana w modelach inwestycji

Model przedstawia pewien fragment rzeczywistości w uproszczony, ale zorganizowany sposób. W modelu matematycznym obiekty systemu (elementy wydzielone pod kątem pewnych interesujących własności) i ich atrybuty (własności obiektu) są przedstawione przez zmienne matematyczne, natomiast działania (procesy wywołujący zmiany w systemie) przez funkcje matematyczne, wzajemnie wiążące ze sobą zmienne.

Istnieje wiele klasyfikacji modeli matematycznych. Przydatnymi w dalszych rozważaniach typologiami modeli matematycznych są:

1. Model statyczny i dynamiczny

2. Model deterministyczny i probabilistyczny

Model statyczny przedstawia zależność między atrybutami systemu w stanie równowagi (w stanie ustalonym). Dynamiczny model matematyczny pozwala na określenie zmian atrybutów systemu jako funkcji czasu. Zależnie od złożoności systemu rozwiązanie dla modeli statycznych zarówn jak i dynamicznych może być analityczne lub numeryczne.

W przypadku gdy wyjście modelu może być w pełni określone za pomocą informacji wejściowych, mamy do czynienia z modelem deterministycznym. Model deterministyczny jest użytecznym i najczęściej stosowanym modelem w opisie wielu zjawisk, m.in. ekonomicznych. Stanowi też ważne narzędzie w procesie optymalizacji, znajdując zastosowanie m.in. w technice, w ekonomii matematycznej i analizach w zarządzaniu. Często ma on formę układu równań różniczkowych bądź różnicowych.

W szczególnych przypadkach małe odchylenia wartości wejściowych mogą prowadzić do dużych zmian w wynikach końcowych. Model o takiej właściwości to model chaosu deterministycznego. Chaotyczność jest silniejszą właściwością od niestabilności rozwiązania. Istnieją równania i układy równań, opisujące model deterministyczny, które dla pewnych, specjalnie dobranych wartości początkowych mają rozwiązania niestabilne. Dla modelu chaosu deterministycznego prawie wszystkie wartości początkowe prowadzą do rozwiązań niestabilnych. Przeprowadzenie dowodu, że model deterministyczny jest chaotyczny, to zadanie trudne, szczególnie w przypadku modeli o skomplikowanej strukturze. Trudno np. uznać model zachowania giełdy za chaotyczny, bo nie udaje się zbudować równań różnicowych czy różniczkowych, opisujących ją w zadowalający sposób. Nie ma więc podstaw do wnioskowania o chaotyczności ich rozwiązań.

W celu badania własności chaosu rozwinięto wiele technik w zakresie analizy równań różniczkowych, np. dla układów chaotycznych korzysta się z przekrojów Poincare. Z własności tych przekrojów wnioskuje się na temat własności pełnej przestrzeni fazowej rozwiązań.

W modelu probabilistycznym wartości zmiennych wejściowych opisują wartości wyjściowe z pewnym prawdopodobieństwem. Zmienne losowe charakteryzują się rozkładem prawdopodobieństwa występowania poszczególnych wartości dla zmiennej dyskretnej lub wartości z poszczególnych przedziałów dla zmiennej ciągłej. Rozkład ten może być stacjonarny, czyli stały w czasie, lub niestacjonarny, czyli zmienny.

Proces stochastyczny to funkcja, której wartości są zmiennymi losowymi. Określa ona zmiany rozkładu prawdopodobieństwa lub funkcji gęstości prawdopodobieństwa w funkcji czasu lub innej zmiennej. Proces stochastyczny jest też definiowany jako rodzina zmiennych losowych. Przykładem procesu stochastycznego jest proces Markowa. W procesie tym rozkład warunkowy zmiennej losowej zależy jedynie od stanu poprzedniego. Proces Markowa zdefiniowany na dyskretnej przestrzeni stanów nazywa się łańcuchem Markowa. Istnieją procesy Markowa z czasem ciągłym. Opracowane przez Kołmogorowa uogólnienie dotyczy przeliczalnie nieskończonych przestrzeni stanów. Pewnym opisem łańcuchów Markowa może być model fizycznego zjawiska ruchów Browna, którego matematycznym modelem jest proces Wienera (w dalszej części pracy utożsamiany z procesem ruchów Browna). Proces Wienera to proces gaussowski, bo zbiór wartości zmiennych losowych ma rozkład normalny.

Niepewność jest pojęciem teorii decyzji. Decyzje powodują różne skutki w zależności od możliwych stanów, których prawdopodobieństwa wystąpienia nie są znane. Rachunek decyzyjny w warunkach niepewności wiąże się z decyzjami, dla których nie jest znany rozkład prawdopodobieństwa ich konsekwencji. Próba praktycznego rozwiązania problemu decyzyjnego w warunkach niepewności zazwyczaj sprowadza się do określenia subiektywnego prawdopodobieństwa zajścia danej konsekwencji.

Z punktu widzenia ekonomii, niepewność jest rozumiana jako problem decyzyjny, w którym określone decyzje powodują różne skutki, w zależności od tego, który z możliwych stanów rzeczy zajdzie. Zakłada się, że znany jest rozkład prawdopodobieństwa wystąpienia określonych stanów rzeczy. Przyjmowane w ekonomii rozwiązanie problemu decyzyjnego w warunkach niepewności ma wskazać takie działanie, które da maksymalną wartość oczekiwaną funkcji celu. W niniejszej pracy mamy do czynienia z takim właśnie przedstawieniem problemu decyzyjnego w zakresie inwestycji w elektroenergetyce. W optymalizacji dynamicznej poszukiwana jest wartość maksymalna z wartości oczekiwanej wskaźnika NPV (wartości zaktualizowanej netto) inwestycji.

Ryzyko oznacza pewną miarę strat, możliwych jako konsekwencja podjęcia decyzji. Wynikiem decyzji jest wystąpienie z pewnym prawdopodobieństwem zdarzenia, które prowadzi do strat. Ryzyko jest więc miarą proporcjonalną do prawdopodobieństwa wystąpienia zdarzenia i do wielkości strat, które może spowodować to zdarzenie. W warunkach ryzyka znane jest prawdopodobieństwo wystąpienia każdej możliwej konsekwencji. Dla matematyków podejmowanie decyzji w warunkach ryzyka to sytuacja, w której znany jest rozkład prawdopodobieństwa skutków każdej możliwej decyzji. Jest to więc sytuacja, którą ekonomiści nazywają rachunkiem decyzyjnym w warunkach niepewności.

4.2.2. Podejmowanie decyzji w warunkach niepewności i ryzyka

Jednym ze źródeł błędów, wynikających z podejmowania decyzji w warunkach niepewności, jest niepewność dotycząca stanu otoczenia projektu inwestycji. Ten rodzaj niepewności, zwany w literaturze jako niepewność strukturalna, uwzględniany jest w programowaniu strukturalnym. Wiele publikacji porusza problem niepewności i zarządzania ryzykiem inwestycyjnym w elektroenergetyce, np. [7, 8, 10, 35, 51, 53, 68, 81, 95].

Ciekawą metodę probabilistycznego podejścia do wartościowania inwestycji w sferze wytwarzania zaproponowano w [76], wykorzystując symulacje Monte-Carlo. Wykazano jednocześnie ograniczenia w tradycyjnym podejściu, operującym całkowitymi kosztami zdyskontowanymi, tzw. levelised cost of electricity LCOE, podczas gdy zliberalizowany rynek energii elektrycznej potrzebuje metod oceny ryzyka inwestycyjnego.

Wśród znanych innych metodyk rachunku decyzyjnego, uwzględniających niepewność jest tzw. real options approach [18, 19, 27, 30, 60, 77, 79, 80], które to podejście umożliwia śledzenie losowo zmieniających się przychodów. Powyższe podejście można wykorzystać szczególnie w przypadku tych inwestycji, które mają charakter nieodwracalnych (tzn. nie mogą być łatwo sprzedane jako produkt rynkowy), a inwestorzy mogą czekać z podjęciem inwestycji na informacje, które zmniejszają niepewność inwestowania. Powyższymi cechami charakteryzują się inwestycje w elektroenergetyce.

Decyzję o inwestowaniu lub odłożeniu jej w czasie należy rozważać jako proces ciągły w czasie, gdyż firma podejmuje decyzję, wdraża ją, a czasem wycofuje się z inwestowania w sposób ciągły w czasie. Natomiast planując inwestycje, należy uwzględnić niepewność dotyczącą cen, kosztów i stopy dyskonta. W dalszych rozważaniach w prezentowanych modelach decyzyjnych uwzględniono niepewność dotyczącą kształtowania się przyszłych przychodów i kosztów inwestycyjnych. Przeanalizowano inwestycję polegającą na budowie elektrowni, biorąc pod uwagę różne technologie wytwarzania energii elektrycznej.

Klasyczne kryterium inwestowania można sprowadzić do badania, czy wskaźnik NPV jest większy od zera, a więc czy zachodzi nierówność
. Równoznaczne jest to badaniu, czy wartość zaktualizowana projektu przewyższa wartość nakładu inwestycyjnego
. Z powyższej nierówności wynika definicja wartości progowej (krytycznej) projektu
, powyżej której należy zrealizować inwestycję. W klasycznym rachunku finansowym wartość progowa wynosi
.

Jeśli jednak uwzględnić niepewność dotyczącą projektu inwestycyjnego, to proces wyznaczania wartości progowej projektu prowadzi do minimalizacji ryzyka inwestycyjnego. Wtedy wartość progowa znacznie różni się od wartości nakładu inwestycyjnego. Progowa wartość zaktualizowana projektu jest związana z progową wartością przychodu z projektu inwestycyjnego
, a zatem jednocześnie z progową wartością przychodu jednostkowego
. Powyższe wartości zależą zarówno od nakładu inwestycyjnego na elektrownię, jak i od ceny oraz kosztu wytwarzania energii elektrycznej i obciążenia elektrowni. Najefektywniejszą technologię wytwarzania energii elektrycznej wskazuje najmniejsza wartość przychodu jednostkowego powiększona o koszt wytwarzania energii elektrycznej dla danej technologii.

W rozdziałach 4.3 i 4.4 opisano metodykę i modele przedstawione w [19, 51], utrzymując identyczne jak w [19] oznaczenia i postaci wzorów.

4.2.3. Ryzyko wytwórcy energii elektrycznej

Konsekwencją podjęcia pewnej decyzji jest możliwość wystąpienia z pewnym prawdopodobieństwem strat. Miarą ryzyka jest wartość oczekiwana wielkości strat, wynikających z podjęcia decyzji. Ryzyko zawsze wiąże się z niebezpieczeństwem straty. Zarządzanie ryzykiem to zespół działań mających na celu obniżenie siły oddziaływania ryzyka na podmiot gospodarczy, w tym przypadku elektrownie, poprzez podejmowanie w tym kierunku optymalnych decyzji [40, 81].

Wyróżnia się dwa podstawowe rodzaje ryzyka: ryzyko spekulatywne, które w zależności od podjętych działań może prowadzić do straty lub zysku i ryzyko czyste, które w zależności od podjętych decyzji może prowadzić do straty lub jej braku. Ten rodzaj ryzyka jest na ogół mierzalny. Zarządzanie ryzykiem zajmuje się ryzykiem czystym.

Robin Kendall dokonał podziału ryzyk w zależności od źródła na ryzyko losowe, w tym katastroficzne, ryzyko quasi-losowe, operacyjne (w zależności od branży ryzyko produkcyjne, technologiczne, projektowe, organizacyjne, proceduralne, związane z zarządzaniem, płynności finansowej itp.), ryzyko rynkowe, kredytowe, prawne, regulacyjne, bankowe i ubezpieczeniowe. Każde z powyższych ryzyk jest istotne dla elektrowni. Listę powyższą można uszczegółowić i ukierunkować na ryzyko dla inwestora w sektorze generacji energii elektrycznej. Dla inwestora i wytwórcy energii elektrycznej w zakresie ryzyka istotny wpływ odgrywa:

1. Ryzyko ceny energii elektrycznej

2. Ryzyko wolumenu sprzedaży energii elektrycznej

3. Ryzyko ceny paliwa

4. Ryzyko kredytowe

5. Ryzyko inwestycyjne

6. Ryzyko losowych uszkodzeń elektrowni

7. Ryzyko ubezpieczeniowe elektrowni

8. Ryzyko środowiskowe

9. Ryzyko polityczne

10. Ryzyko kursu walut

Analizie podlegają te rodzaje ryzyka, które można w sposób wiarygodny kwantyfikować [53]. Jedna z koncepcji mierzenia ryzyka oparta jest na mierze Value at Risk (VaR) - tzw. wartości zagrożonej. Miara ta może być zaadaptowana na potrzeby przedsiębiorstwa w celu określenia następujących miar:

1. Earnings at Risk (EaR) - „zysk zagrożony”

2. Cash Flow at Risk (CFaR) - „przepływ pieniężny zagrożony”

Miara EaR to górna wielkość, o którą może być mniejszy zysk netto przedsiębiorstwa w wypadku zrealizowania się zdarzeń niekorzystnych.

Zaproponowany w pracy sposób wyznaczania krytycznej wartości projektu inwestycyjnego minimalizuje ryzyko rynkowe, którego składnikami są: ryzyko ceny energii elektrycznej, ryzyko ceny paliwa, ryzyko wolumenu sprzedaży energii elektrycznej i ryzyko inwestycyjne.

4.2.4. Kryterium porównywania efektywności ekonomicznej różnych technologii wytwarzania energii elektrycznej

Podstawową metodą porównywania wariantów rozwiązań technicznych w elektroenergetyce była metoda opracowana przez K. Kopeckiego [45], bazująca na rocznych kosztach eksploatacyjnych. Metoda spopularyzowała stosowanie rachunku dyskonta. Jako kryterium wyboru spośród porównywanych wariantów inwestycji w nowe źródła energii elektrycznej przyjęto minimum jednostkowego kosztu rocznego produkcji energii elektrycznej, określonego jako iloraz rocznych kosztów eksploatacyjnych i rocznej produkcji energii elektrycznej netto. Koszty ponoszone w kolejnych latach eksploatacji elektrowni należy sprowadzić rachunkiem dyskonta do tzw. równoważnych (ekwiwalentnych) kosztów rocznych. Wybór optymalnego rozwiązania polega na wybraniu wariantu, dla którego równoważne koszty roczne są najmniejsze. Kontynuacją i rozwinięciem powyższej metody były prace prowadzone przez S. Górę, J. Mareckiego i C. Mejro [25, 61]. W latach osiemdziesiątych ubiegłego wieku zalecanym podejściem było planowanie według najmniejszych kosztów tzw. Least-Cost Planning (LCP). W opracowanym przez M. Kwiatkowskiego i R. Krochmalskiego „Studium rozwoju podsystemu wytwarzania energii elektrycznej do 2020 r.” podjęto analizę problemów modernizacji elektrowni w systemie. Zastosowane oprogramowanie WASP III zostało opracowane przez Argon National Laboratories w Chicago i Międzynarodową Agencję Energii Atomowej (IAEA) w Wiedniu pod auspicjami Banku Światowego. Oprogramowanie WASP III umożliwiło wybór optymalnego planu rozwoju systemu elektroenergetycznego. Kontynuacja badań w PSE S.A. pod nadzorem R. Janiczka doprowadziła do realizacji zintegrowanego programowania rozwoju systemu elektroenergetycznego w wersji ZPR-1, ZPR-2 i ZPR2+. W ostatnich latach problematykę optymalnego rachunku ekonomicznego w elektroenergetyce rozwija m.in. D. Laudyn [56], B. Zaporowski [96, 97].

W gospodarce rynkowej miernikiem efektu rozwiązania technicznego jest zysk, a celem działalności gospodarczej maksymalizacja zysku. Jeśli cenę kształtują mechanizmy rynku, czyli jeśli jest ona wynikiem walki konkurencyjnej na rynku energii elektrycznej, to maksymalizacja zysku związana jest z minimalizacją kosztu własnego wytwarzania energii elektrycznej.

Dodatkowym narzędziem analizy ekonomicznej przedsięwzięć inwestycyjnych jest analiza niepewności i ryzyka. Niepewność dotyczy kształtowania się wielkości wejściowych, przyjętych do obliczeń ekonomicznych oraz ich zmian w czasie. Niepewność jest funkcją czasu, zwiększając się przy wydłużaniu rozważanego horyzontu czasowego. Ryzyko rozumiane jest jako możliwość poniesienia straty.

Metody porównywania wariantów rozwiązań technicznych bazujące na strumieniach pieniężnych w okresie eksploatacji budzą wątpliwości, gdyż wymagają przewidywania kształtowania się kosztów paliwa i materiałów pomocniczych, płac, kosztów użytkowania środowiska itp. w horyzoncie długoterminowym. Mankamenty powyższe znacznie ogranicza metoda opcyjna, wykorzystująca wskaźnik NPV z uwzględnieniem niepewności i ryzyka.

Analizowane warianty rozwiązań technicznych muszą spełniać warunki równoważności pod względem:

1. efektu, tj. produkcji energii elektrycznej,

2. jakości produkcji,

3. niezawodności i dyspozycyjności produkcji,

4. okresu użytkowania.

Różnice w czasowym rozkładzie nakładów inwestycyjnych, produkcji energii elektrycznej i okresu użytkowania elektrowni są sprowadzane do równoważności rachunkiem dyskonta. Dla każdej elektrowni systemowej założono identyczny stopień wyzyskania mocy zainstalowanej. W analizie wykorzystano tylko te rodzaje elektrowni systemowych, które charakteryzują się podobną dyspozycyjnością, wyłączając np. elektrownie wodne i wiatrowe. Z uwagi na różnice w mocach zainstalowanych analizowanych bloków należało opracować metodę postępowania w ocenie efektywności ekonomicznej w analizie porównawczej. Optymalizacja dynamiczna z funkcją celu w postaci szukania maksimum wartości oczekiwanej wskaźnika NPV w analizie opcyjnej, tzw. real options approach, nie zapewnia równoważności w postaci identycznej produkcji energii elektrycznej. Zmusza to do sformułowania kryterium porównawczego w postaci szukania wśród technologii minimalnej wartości krytycznej ceny energii elektrycznej na rynku hurtowym zapewniającej zwrot nakładów inwestycyjnych. Na cenę krytyczną
składa się koszt własny wytwarzania energii elektrycznej bez uwzględnienia w tym koszcie nakładów inwestycyjnych, czyli suma kosztów prowadzenia ruchu, remontów oraz paliwa
i przychód jednostkowy
, zapewniający zwrot nakładów inwestycyjnych. Cenę krytyczną należy powiększyć o koszty zewnętrzne
w celu uwzględnienia dodatkowych kosztów (w tym przypadku kosztów związanych z emisją CO₂). Można zapisać, że cena krytyczna dla j-tej technologii bez uwzględnienia kosztów zewnętrznych wynosi:

(4.11)

Kryterium wyboru najefektywniejszej technologii z uwzględnieniem kosztów zewnętrznych to wybór technologii o najniższej cenie krytycznej powiększonej o koszty zewnętrzne. Sformułowane kryterium przybiera postać:

(4.12)

4.3. Podstawy teoretyczne optymalizacji dynamicznej procesów ciągłych w warunkach niepewności

4.3.1. Sformułowanie problemu

Czas odgrywa ważną rolę w procesie podejmowania decyzji o inwestycjach. Przyszły strumień wpływów pieniężnych z inwestycji obarczony jest niepewnością, której źródłem są m.in. przyszłe decyzje firmy oraz jej konkurentów. Jedną z możliwości ograniczenia niepewności jest odłożenie w czasie decyzji o podjęciu inwestycji. W matematycznym modelowaniu inwestycji rozwijanym w dalszej części pracy zostanie uwzględniona ta możliwość.

Do rozwiązania powyższego problemu można wykorzystać programowanie dynamiczne. Programowanie dynamiczne jest bardzo pomocnym narzędziem optymalizacji dynamicznej i umożliwia w analizach uwzględnienie niepewności.

Jeśli rozważania prowadzi się dla przypadku procesu decyzyjnego ciągłego w czasie, to niepewność można zamodelować procesem Wienera. Większość procesów decyzyjnych w elektroenergetyce opisują jednak wielkości w postaci dyskretnej. W modelach przedstawiających powyższe procesy niepewność modeluje się za pomocą procesów Markowa. Zawsze jednak można proces w postaci dyskretnej aproksymować i sprowadzić w ten sposób zagadnienie do programowania procesu ciągłego. Z tego powodu w pracy rozważa się proces decyzyjny ciągły w czasie. Poniżej przedstawiono ideę programowania dynamicznego, wychodząc od procesu dyskretnego, z uwagi na prostotę wnioskowania, a następnie przekształcono zagadnienie do programowania procesu ciągłego. Metodyka jest ogólnie znana i opisywana w literaturze, przedstawiany zapis zgodny jest z prezentowanym w [19].

Przyjmijmy, że przychody elektrowni opisuje zmienna stanu X. Dla pewnej chwili czasowej t aktualna wartość x_t jest znana, ale przyszłe realizacje x_t+1, x_t+2,... są wartościami losowymi stanowiącymi proces Markowa. Stan aktualny jest opisany przez rozkład zmiennej X. W każdej chwili czasowej t możliwe są do wyboru pewne strategie, które reprezentuje zmienna sterująca u. Może ona być w ogólności zmienną binarną, ciągłą lub wektorem. W rozważanym zagadnieniu przyjęto, że zmienna sterująca jest zmienną binarną, przyjmującą wartość 0 w przypadku, gdy decyzja jest „oczekiwać”, lub wartość 1 w przypadku, gdy decyzja jest „inwestować natychmiast”. Wartość zmiennej u_t musi być wyznaczona tylko na podstawie informacji dostępnych dla chwili czasowej t. Stan systemu, zdeterminowany wartością zmiennej x_t oraz zmiennej sterującej u_t, implikuje przychód oznaczony π_t(x_t,u_t). Niech
oznacza warunkowe skumulowane prawdopodobieństwo rozkładu zmiennej stanu. Czynnik dyskontujący między dwoma okresami wynosi
, gdzie ρ - stopa dyskonta. Celem modelu jest wybór sekwencji wartości zmiennej sterującej
w taki sposób, aby maksymalizować wartość zaktualizowaną netto przychodów. Czasem można wymóc zakończenie procesu w pewnym okresie T z końcową wypłatą
, która zależy od osiągniętego stanu
. Założono, że startową (początkową) chwilą czasu jest t. Oznaczono F_t(x_t) oczekiwaną wartość zaktualizowaną netto wszystkich przepływów pieniężnych elektrowni. Równanie Bellmana przyjmie więc postać:

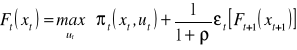
(4.13)

Pierwszy składnik prawej strony oznacza natychmiastowy przychód, drugi składnik wartość kontynuacji.

Jeśli problem wielookresowy ma skończony, ustalony horyzont czasowy T, to można wówczas, poszukując rozwiązania wystartować w chwili T i cofać się. W chwili czasu T elektrownia uzyskuje końcową wypłatę
. Wtedy w chwili o jeden przedział czasu wstecz, czyli T-1, mamy:

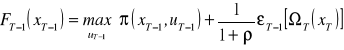
(4.14)

Równanie (4.14) umożliwia znalezienie wartość funkcji w T-1. Skorzystanie z równania (4.13) prowadzi w dalszym postępowaniu do procedury iteracyjnej i pozwala rozwiązać problem optymalizacji dla u_T-2, wyznaczając wartość funkcji F_T-2(x_T-2) itd. Postęp w technice komputerowej umożliwia rozwiązanie powyższego problemu numerycznie.

1. Horyzont nieskończony

Podstawowym uproszczeniem w przypadku nieskończonego horyzontu jest niezależność procedury obliczeniowej od czasu t. Wartość funkcji jest identyczna dla każdego okresu, mimo że jest szacowana dla różnych wartości x_t. Wartości x_t oraz x_t+1 mogą być dowolnymi z możliwych stanów. Uogólniając powyższe wartości jako x i x^', równanie Bellmana przybiera formę:

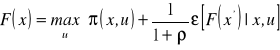
(4.15)

Równanie to przybiera formę równania funkcjonalnego, w którym wszystkie funkcje F są nieznane. Rozwiązywanie równania prowadzi do procedury iteracyjnej. Startując od zakładanej jako rozwiązanie wartości
z powyższego równania można wyznaczyć odpowiadającą jej optymalną wartość
, która może być wyrażona jako funkcja zmiennej x. Podstawiając ją ponownie prawa strona wyraża nową funkcję
. Podstawiając ją jako następne rozwiązanie, powtarzamy procedurę, otrzymując kolejno
itd. przybliżając wartość rozwiązania. Procedura jest zbieżna niezależnie od wybranej funkcji startowej i umożliwia osiągnięcie wymaganej dokładności aproksymacji w skończonej liczbie iteracji.

4.3.3. Optymalny stop

W prostym modelu inwestycji, gdy wybór w każdym okresie ma charakter binarny, stop oznacza podjęcie inwestycji, a kontynuacja procesu oznacza oczekiwanie. W przypadku analizy elektrowni kontynuacja nie generuje przepływów pieniężnych, ale nie jest to regułą.

Niech
oznacza strumień przychodów, a
wypłatę przy zatrzymaniu, czyli podjęciu inwestycji. Wtedy równanie Bellmana przybiera postać:

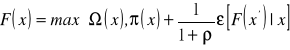
(4.16)

Można wyznaczyć wartość krytyczną x^*, dla której kontynuacja jest optymalna, gdy x>x^* , a stop, gdy x<x^*. Aby kontynuacja była atrakcyjniejszą opcją dla większych wartości x , to natychmiastowa korzyść z kontynuacji powinna wzrastać szybciej niż wartość wypłaty
. Różnica
powinna wzrastać, jeśli x zwiększa się.

4.3.4. Proces ciągły

Dla przedziałów czasowych o długości Δt przychód jednostkowy oznaczmy
. Jeśli
oznacza stopę dyskonta w jednostce czasu, to odpowiadający czasowi Δt współczynnik dyskonta równy jest
. Równanie Bellmana przyjmie wtedy postać:

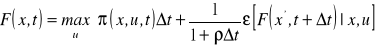
(4.17)

Mnożąc przez
obie strony równania (4.17) i przenosząc F(x,t) na prawą stronę, uzyskuje się:

(4.18)

lub

(4.19)

Dzieląc obie strony przez Δt i znajdując granicę przy Δt→0 dochodzimy do równania:

(4.20)

Ta forma równania Bellmana po lewej stronie zawiera zwrot w jednostce czasu. Po prawej stronie pierwszy składnik oznacza natychmiastową wypłatę lub dywidendę z oszacowania aktywów, podczas gdy drugi składnik to oczekiwana rata zysku (straty, jeśli wartość ujemna).

Wartość maksymalna zależy od oczekiwanej wartości zmiennej losowej x^' w kolejnych chwilach czasowych Δt. Dwie klasy stochastycznych procesów ciągłych w czasie: procesy Ito i procesy Poissona umożliwiają w prosty sposób wyznaczenie rozwiązania dla funkcji F(x,t). Powyższe procesy są przydatne w wielu zastosowaniach ekonomicznych, a podstawy matematyczne szczegółowo opisane w [41].

4.3.5. Procesy Ito

Rozważmy zmiany zmiennej losowej X w postaci:

(4.21)

gdzie:

dz - inkrement standardowego procesu Wienera.

Lemat Ito podaje wzór na różniczkę dF jako:

(4.22)

Rozwijając wzór (4.22) poprzez podstawienie za dx zależności ze wzoru (4.21), otrzymujemy:

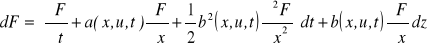
(4.23)

Wykorzystując lemat Ito do wyznaczenia wartości oczekiwanej funkcji F, można zapisać:

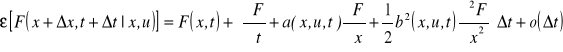
(4.24)

Składnik
reprezentuje resztę, która dąży do zera szybciej niż Δt. Równanie (4.20) przyjmuje więc postać:

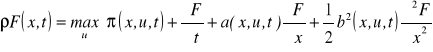
(4.25)

Otrzymano równanie różniczkowe cząstkowe drugiego rzędu z funkcją F jako zmienną zależną, a zmiennymi x i t jako zmiennymi niezależnymi. W wielu zastosowaniach możliwe jest znalezienie rozwiązania na drodze analitycznej lub numerycznie. Warunkiem brzegowym jest dla x równanie:

(4.26)

Jeśli rozważany horyzont czasu jest nieskończony i funkcje π, a i b nie zależą od czasu, to wtedy równanie (4.25) staje się zwykłym równaniem różniczkowym z jedną zmienną niezależną x:

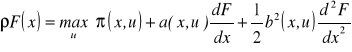
(4.27)

4.4. Modele podejmowania decyzji o inwestowaniu w elektroenergetyce

4.4.1. Model McDonalda i Siegela

4.4.1.1. Ogólny opis modelu

Prezentowany model jest jednym z najprostszych modeli ciągłych nieodwracalnej inwestycji. W tym modelu, który został opracowany przez McDonalda i Siegela (1986), firma musi zdecydować, kiedy zainwestować w pojedynczy projekt. W niniejszym rozdziale przedstawiono założenia metodyczne modelu McDonalda i Siegela na podstawie [19, 60].

Koszt inwestycji I jest znany i ustalony, ale wartość projektu V zmienia się zgodnie z modelem geometrycznych ruchów Browna. W takim ujęciu klasyczne kryterium inwestowania oparte na wartości zaktualizowanej netto NPV, prowadząc do warunku V>I, powoduje często znaczne błędy. Model McDonalda i Siegela ma za zadanie wskazać optymalną wartość kosztów inwestycji I, które zostaną zwrócone przy wartości projektu V, zmieniającej się zgodnie z równaniem (4.21) procesu Wienera, przyjmując postać:

(4.28)

gdzie:

dz - przyrost procesu Wienera

α - współczynnik trendu,

σ - odchylenie standardowe.

Postać modelu wskazuje, że aktualna wartość projektu jest znana, ale przyszłe realizacje mają rozkład lognormalny z wariancją liniowo wzrastającą w czasie. Założono więc, że wartość projektu jest wielkością niestacjonarną.

Wartość opcji inwestowania oznaczono F(V). Jest to wartość maksymalna z oczekiwanej wartości zaktualizowanej inwestycji:

(4.29)

gdzie:

ε - oznaczenie wartości oczekiwanej,

T - czas, w którym inwestycja ma być oddana do użytkowania,

ρ - stopa dyskonta.

Aby rozwiązanie miało sens, należy założyć, że α < ρ, czyli

(4.30)

4.4.1.2. Zmienność przychodów zdeterminowana

W pierwszym etapie rozważań założono brak niepewności dotyczącą wartości projektu, czyli w równaniu (4.28) przyjęto σ = 0. Implikuje to następujący przebieg czasowy wartości projektu:

(4.31)

Wartość opcji inwestowania można wtedy zapisać następująco:

(4.32)

Poszukując maksimum wartości opcji inwestowania F(V) w funkcji chwili czasowej podjęcia inwestycji T, z warunku koniecznego istnienia ekstremum

(4.33)

otrzymano:

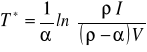
(4.34)

Szukając wartości projektu V^*, powyżej której opłaca się inwestować natychmiast, należy we wzorze (4.34) przyjąć T^*= 0, co implikuje zależność:

(4.35)

4.4.1.3. Zmienność przychodów stochastyczna

Powróćmy do ogólnych rozważań z uwzględnieniem niepewności, czyli σ>0. Również i w tym przypadku należy wyznaczyć wartość progową projektu V^*, dla której opłaca się inwestować natychmiast. Założono brak przychodu π w okresie przed realizacją inwestycji. Wtedy równanie Bellmana (4.20) przyjmuje postać:

(4.36)

Oznaczmy:

Z lematu Ito wynika:

(4.37)

Wstawiając równanie (4.28) do (4.37) i przyjmując , uzyskujemy:

(4.38)

Równanie Bellmana (4.36) można zatem zapisać w postaci:

(4.39)

lub

(4.40)

Dodatkowo F(V) musi spełniać warunki brzegowe:

(4.41)

(4.42)

(4.43)

Aby spełniać warunek (4.41), rozwiązanie przewiduje się w postaci:

(4.44)

Stałą A oraz wartość progową V^* można wyznaczyć podstawiając (4.44) do (4.42) i (4.43). Otrzymano w [19]:

(4.45)

i

(4.46)

Równanie (4.45) wskazuje, że klasyczne prawo teorii inwestowania oparte na wartości zaktualizowanej inwestycji netto NPV może prowadzić do błędnych decyzji, jeśli nie uwzględnia się niepewności.

Podstawiając funkcję (4.44) oraz pierwszą i drugą pochodną do równania (4.40) otrzymano równanie charakterystyczne równania różniczkowego w postaci:

(4.47)

Dwoma pierwiastkami tego równania są:

(4.48)

(4.49)

Z analizy powyższych wielkości wynika, że β₁>1 i β₂<0. Ogólne rozwiązanie równania (4.40) można przewidywać w postaci:

(4.50)

gdzie: A₁, A₂ - stałe.

Z warunków brzegowych (4.41)÷(4.43) dla rozważanego zagadnienia wynika, że A₂ = 0 i rozwiązanie przyjmuje postać równania (4.44).

1. Inwestycja z wartością projektu zależną od ceny energii elektrycznej

4.4.2.1. Postać modelu

Inwestycja tego typu po zrealizowaniu generuje zmienny, wyjściowy przepływ pieniężny. Dla prostoty dalszych rozważań przyjęto, że wielkość wyjściowa produkcji to jedna umowna jednostka produktu w ciągu roku o cenie P. Założono ponadto w [19], że z krzywej popytu wynika cena, będąca funkcją podaży Q, i przyjmuje ona postać

(4.51)

gdzie:

Y - zmienna stochastyczna.

W analizie inwestycji w elektroenergetyce nie można jednak ignorować kosztów produkcji energii elektrycznej, bo stanowią one istotny składnik, wpływający na rentowność produkcji. Dlatego też w niniejszej analizie przyjęto założenie, że pod pojęciem ceny rozumiany jest przychód, wyznaczony jako różnica ceny i kosztu wytwarzania energii elektrycznej. Przy powyższym założeniu przychód elektrowni można oszacować jako

(4.52)

Z zależności (4.52) wynika, że zmienną P można traktować jako zmienną stochastyczną. Najprościej zamodelować zmiany P modelem geometrycznych ruchów Browna z trendem:

(4.53)

Przychód z projektu inwestycyjnego zmienia się z trendem o współczynniku zmian równym α, a przyszłe przychody są dyskontowane stopą równą μ (stopa uwzględniająca ryzyko rynkowe inwestora, wyznaczona na podstawie modelu CAPM [9]). Wtedy oczekiwana wartość zaktualizowana V projektu wynosi:

(4.54)

Z powyższego zapisu wynika, że wartość projektu jest procesem stochastycznym wyrażonym równaniem analogicznym do (4.53) z parametrami α i σ.

4.4.2.2. Wyznaczanie wartości projektu inwestycyjnego

Wartość projektu jest przypadkowym i pochodnym aktywem, który zależy od elementarnego aktywu, jakim jest wartość przychodu P. Z tego powodu wartość projektu zostanie wyznaczona jako funkcja przychodu podstawowego aktywu V(P). W [19] uzyskuje się równanie różniczkowe:

(4.55)

Równanie jednorodne ma rozwiązanie w postaci:

(4.56)

gdzie: β jest pierwiastkiem równania charakterystycznego:

(4.57)

Dla r>0 i δ>0 dwa pierwiastki spełniają nierówności
i
.

Ogólne rozwiązanie równania niejednorodnego przybiera formę:

(4.58)

Ostatni składnik rozwiązania to oczekiwana wartość zaktualizowana strumienia przychodów
, gdy wartością początkową są przychody na poziomie P. Jeśli wartość oczekiwana przychodów wynosi:

(4.59)

to oczekiwana wartość zaktualizowana jest równa:

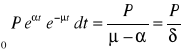
(4.60)

Ekonomiczna analiza procesu prowadzi do wniosku, że:

(4.61)

co implikuje wartość współczynnika
:

(4.62)

4.4.2.3. Wartościowanie opcji inwestowania

Wartość opcji inwestowania F stosunkowo łatwo wyznaczyć jako funkcję przychodu P, wykorzystując wyznaczone powyżej rozwiązanie
dla warunków brzegowych. Analogiczne rozumowanie do przeprowadzonego w poprzednim rozdziale prowadzi do uzyskania w [19] następującego równania różniczkowego:

(4.63)

Opcja inwestowania oczywiście nie generuje dywidendy, dlatego uzyskano równanie jednorodne drugiego rzędu. Rozwiązanie można zakładać jako kombinację liniową dwu liniowo niezależnych rozwiązań:

(4.64)

- współczynniki, których wartości należy wyznaczyć.

Ponieważ wyższe wartości przychodu P czynią opcję inwestowania atrakcyjniejszą, stąd należy wyznaczyć wartość graniczną
, powyżej której opłaca się inwestować natychmiast.

Z warunku:

(4.65)

wynika wartość współczynnika
:

(4.66)

Wartość opcji inwestowania musi równać się wartości zaktualizowanej inwestycji:

(4.67)

Wykresy
i
powinny być styczne w punkcie
, czyli:

(4.68)

Z powyższych warunków można wyznaczyć:

(4.69)

oraz

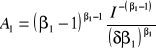
(4.70)

Korzystając z zależności (4.54), można więc zapisać:

(4.71)

Wartość projektu jest w tym przypadku wprost proporcjonalna do przychodu, gdyż
.

4.4.2.4. Programowanie dynamiczne dla wartości projektu zależnego od ceny

Jeżeli niepewność oszacowania przyszłych przychodów P ze sprzedaży energii elektrycznej nie może być pominięta, to w celu wyznaczenia wartości projektu inwestycyjnego V(P) oraz wartości krytycznych projektu i przychodu można wykorzystać optymalizację dynamiczną, zakładając wartość stopy dyskonta ρ, uwzględniającą ryzyko finansowe oraz biznesowe. Wartość projektu w czasie t może być przedstawiona jako suma przepływu pieniężnego w przedziale czasu (t, t+dt) i wartości kontynuacji po tym czasie:

(4.72)

Wykorzystując lemat Ito, otrzymuje się równanie:

(4.73)

gdzie:

- składnik resztowy dążący do zera szybciej niż dt.

Upraszczając powyższe równanie, dzieląc przez dt i następnie wyznaczając granicę przy
, otrzymuje się równanie różniczkowe:

(4.74)

Z równania łatwo uzyskać rozwiązanie w postaci:

(4.75)

dla

Opcja inwestowania może być podobnie analizowana. Uzyskuje się równanie różniczkowe:

(4.76)

W rezultacie wg [19] wartość krytyczna przybiera postać:

(4.77)

4.4.3. Uwzględnianie kosztów eksploatacyjnych i czasowego zawieszenia eksploatacji elektrowni

4.4.3.1. Wartość projektu

Założono, że eksploatacja elektrowni związana jest z kosztami C oraz że eksploatacja może być czasowo zawieszona bez znaczących, dodatkowych kosztów, jeśli przepływ pieniężny P obniży się poniżej wartości kosztów C. Możliwe jest ponowne uruchomienie produkcji, jeśli przepływ P zwiększy się powyżej wartości C. Wtedy przychody z projektu można zapisać jako:

(4.78)

Rozważa się krótki przedział czasu (t, t+dt). Jednostkowy przychód wynosi
, stąd równanie różniczkowe dla wartości projektu przybiera wg [19] postać:

(4.79)

Z uwagi na wartość przychodu rozwiązanie równania należy wyznaczyć dla dwóch przedziałów, gdy
oraz gdy
, i następnie przeprowadzić dyskusję rozwiązania dla
.

Dla
wartość
i równanie różniczkowe staje się równaniem jednorodnym, którego rozwiązanie jest liniową kombinacją dwu składników odpowiadających dwóm pierwiastkom równania charakterystycznego:

(4.80)

gdzie:

- stałe.

Dla
do rozwiązania równania jednorodnego należy dodać szczególne rozwiązanie pełnego równania. Równanie jest spełnione dla prostego podstawienia
. Stąd rozwiązanie ogólne przybiera postać:

(4.81)

gdzie:

- stałe.

Dla
z warunków brzegowych wynika, że
.

Dla
, gdy P staje się bardzo duże, to opcja oczekiwania jest mało prawdopodobna, toteż jej wartość powinna być równa zeru. Stąd
, a rozwiązanie można zapisać w postaci:

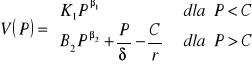
(4.82)

Stałe
można wyznaczyć z warunku, że w punkcie
rozwiązanie musi być ciągłe i różniczkowalne:

(4.83)

(4.84)

Powyższy układ równań ma rozwiązanie:

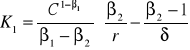
(4.85)

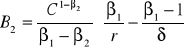
(4.86)

1. Wartość opcji inwestowania

Wartość opcji inwestowania F(P) określa optymalną strategię inwestowania. Zakładając, że przychód P zmienia się zgodnie z modelem ruchów Browna, można przeprowadzić podobne rozumowanie do rozumowania w poprzednim rozdziale i uzyskać rozwiązanie dla opcji inwestowania w postaci:

(4.87)

Dla
wartość
, co implikuje
. Optymalnego rozwiązania
należy poszukiwać dla przedziału
. Z warunku dopasowania wartości i warunku ciągłości uzyskuje się układ równań z dwiema niewiadomymi
i
:

(4.88)

(4.89)

Po wyrugowaniu
uzyskuje się równanie z jedną niewiadomą
, które można rozwiązać numerycznie:

(4.90)

4.4.3.3. Projekt ze zmiennym wyjściem

W wielu rzeczywistych sytuacjach gospodarczych, w tym w projektach inwestycyjnych w nowe technologie wytwarzania energii elektrycznej, koszty zmienne zależą od wielu chwilowych wartości składowych, tj. kosztów osobowych, kosztów eksploatacyjnych, czy remontów, które można uzależnić od wartości ceny P. W rezultacie przepływy przychodów elektrowni także zależą od ceny P.

W dowolnej chwili czasowej koszty zmienne zależą od wyboru wektora zmiennych v, czyli kosztów osobowych, eksploatacyjnych itp. Wybór wektora wpływa na wartość wyjściową projektu, zgodnie z funkcją produkcji
, oraz na koszty zmienne
. Optymalny wybór wektora v maksymalizuje funkcję przychodu, co można zapisać w postaci:

(4.91)

Powyższa funkcja jest uogólnieniem funkcji rozważanej w poprzednim rozdziale. Przyjęcie założenia, że zmienna v przyjmuje jedną z dwu wartości 0 lub 1, dla których zdefiniowano funkcje:

(4.92)

doprowadza do określenia funkcji przychodu w postaci (4.78).

Innym popularnym modelem jest funkcja produkcji Cobba-Douglasa, którą można zapisać w poniższej postaci, przyjmując, że v jest skalarem:

(4.93)

Uwzględniając niepewność ceny poprzez stałą c, maksymalizacja przychodu prowadzi do określenia wejściowej funkcji popytu:

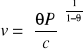
(4.94)

i wyjściowej funkcji podaży:

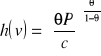
(4.95)

Dla wybranej optymalnej wartości zmiennej wejściowej można wyznaczyć przychód:

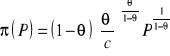
(4.96)

Upraszczając zapis, uzyskano:

(4.97)

gdzie:

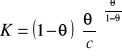
W powyższym równaniu wykładnik γ > 1.

Podobne rozumowanie jak w poprzednim rozdziale prowadzi do równania różniczkowego podanego w [19] w postaci:

(4.98)

którego rozwiązanie przewidywane jest w postaci:

(4.99)

Z warunków brzegowych wynika rozwiązanie:

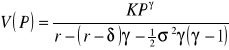
(4.100)

Równanie powyższe ma prostą ekonomiczną interpretację, gdyż stanowi oczekiwaną wartość zaktualizowaną strumienia wpływów
. Wartość projektu można zatem zapisać w postaci:

(4.101)

Aby powyższy zapis miał sens, musi być spełniony warunek, aby wartość
. Implikuje to nierówność
.

Rozwiązanie dla wartości opcji inwestowania przybiera postać:

(4.102)

Wartość opcji inwestowania musi równać się wartości zaktualizowanej inwestycji:

(4.103)

Wykresy
i
powinny być styczne w punkcie
, czyli:

(4.104)

Z powyższych warunków można wyznaczyć wartość progową ceny, powyżej której opłaca się inwestować natychmiast:

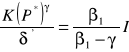
(4.105)

Literatura

1. Armor A.F., Viswanathan R., Dalton S.M., Annendyck H.: Ultrasupercritical Steam Turbines: Design and Materials Issues for the next Generation, VGB Konferenz “Kraftwerke im Wettbewerb-Technik, Betrieb und Umwelt” Kolonia, marzec 2003.

2. Bartnik R., Popławski J.: Ocena efektywności ekonomicznej elektrociepłowni gazowo-parowej, Energetyka, Nr 7, 1997 s.307-313

3. Bartnik R.: Uwarunkowania stosowania w kraju nowoczesnych technologii skojarzonego wytwarzania ciepła i energii elektrycznej opartych na spalaniu gazu ziemnego, Energetyka, nr 1/2000

4. Bartnik R.: Analiza termodynamiczna i ekonomiczna skojarzonego wytwarzania ciepła i energii elektrycznej w układach gazowo-parowych, Zeszyty Naukowe Politechniki Śląskiej, s. Energetyka, z.136, Gliwice 2002

5. Bartnik R.: Rachunek efektywności techniczno-ekonomicznej w energetyce zawodowej, Oficyna Wydawnicza Politechniki Opolskiej, Opole 2008

6. Barzyk G., Szwed P.: Małe elektrownie wiatrowe jako źródła generacji rozproszonej, mat. konf. XII Międzynarodowa Konferencja Naukowa „Aktualne Problemy w Elektroenergetyce” APE'2005, Gdańsk-Jurata, 8-10 czerwca 2005, Tom IV, s.3-9

7. Bogacz J., Gwóźdź R., Przygrodzki M.: Ocena efektywności ekonomicznej inwestycji sieciowych, mat. konf. XII Międzynarodowa Konferencja Naukowa „Aktualne Problemy w Elektroenergetyce” APE'2005, Gdańsk-Jurata, 8-10 czerwca 2005, Tom III, s.179-186.

8. Botterud A., Ilic M.D., Wagensteen I.: Optimal Investments in Power Generation Under Centralized and Decentralized Decision Making, IEEE Transactions on Power Systems, February 2005, Vol. 20, N^o 1, p.254-263, ISSN 0885-8950

9. Brealey R., Myers S.: Principles of Corporate Finance, McGraw-Hill, Inc., 1981.

10. Buchta F.: O zastosowaniu równoważnika pewności do oceny ryzyka decyzji rozwojowych w sieci przesyłowej, mat. konf. XII Międzynarodowa Konferencja Naukowa „Aktualne Problemy w Elektroenergetyce” APE'2005, Gdańsk-Jurata, 8-10 czerwca 2005, Tom III, s.11-18

11. Celiński Z., Strupczewski A.: Podstawy energetyki jądrowej, WNT, Warszawa, 1984.

12. Chmielniak T.,: Nowe technologie wykorzystania pierwotnych stałych nośników energii, Polityka Energetyczna, Tom 10, PAN, Kraków 2007.

13. Chmielniak T.: Nowe technologie energetyczne, Archiwum Energetyki, t. XXXVI, 2006.

14. Chmielniak T.: Technologie energetyczne, WNT Warszawa, 2008

15. Ciechanowicz W.: Bioenergia a energia jądrowa, Wyższa Szkoła Informatyki Stosowanej i Zarządzania, Warszawa 2001, ISBN 83-88311-33-6

16. Ciechanowicz W., Szczukowski S.: Ogniwa paliwowe i biomasa lignocelulozowa szansą rozwoju wsi i miast, Wyższa Szkoła Informatyki Stosowanej i Zarządzania, Warszawa 2003, ISBN 83-88311-67-0

17. Dąbkowski M., Efektywność inwestycji według Banku Światowego, Wydawca Centrum Informacji Menedżera, Warszawa 1992.

18. Dixit A.K.: Investment and Hysteresis, Journal of Economic Perspectives, Winter, 1992, pp.107-132.

19. Dixit A.K., Pindyck R.S.: Investment under Uncertainty, Princeton University Press 1994

20. Engstrőm F.: Overview of Power Generation from Biomass, Gasification Technology Conference, San Francisco, October 1999.

21. Falsetti J.S. i in.: From Coal or Oil to 550 MWe via 9H IGCC, Gasification Technology Conference, San Francisco, October 2000.

22. Filipowicz M: Generatory magnetohydrodynamiczne. Wyższa wydajność MHD, Nafta & Gaz Biznes, wrzesień 2004

23. Gas Turbine World 2001-2002 Handbook, A Pequot Publication, vol. 22.

24. Golec T., Rakowski J., Świrski J.: Perspektywy postępu technicznego w wytwarzaniu energii elektrycznej przy wykorzystaniu węgla kamiennego, węgla brunatnego i gazu ziemnego z uwzględnieniem efektu środowiskowego, Elektroenergetyka nr 1/2004 (48), str.16-26.

25. Góra S., Kopecki K., Marecki J., Pochyluk R.: Zbiór zadań z gospodarki elektroenergetycznej, PWN, Warszawa, 1976.

26. Halawa T.: Postęp w budowie bloków energetycznych dużej mocy opalanych węglem brunatnym, Energetyka, grudzień 2007

27. Hedman K.W., Gao F., Sheble G.B.: Overview of transmission expansion planning using real options analysis, presented at the Proceedings of 37^th Annual North American Power Symposium, 2005, pp.497-502

28. Heitmüller R.J., Fischer H., Sigg J., Bell R.M., Hartlieb N.: Lignite-fired Niederaussem aims for efficiency of 45% and more, Modern Power Systems, May 1999, pp.53-66.

29. Rozporządzenie Ministra Środowiska z dnia 04 sierpnia 2003 w sprawie standardów emisyjnych, Dziennik Ustaw 2003, Nr 169, poz. 1584

30. Herbelot O.: Option Valuation of Flexible Investments: The Case of Environmental Investments in the Electric Power Industry, unpublished Ph.D. dissertation, Massachusetts Institute of Technology, May 1992

31. Holt N.: Gasification Technology Status, December 1999, niepublikowany materiał EPRI.

32. Husemann R.H.: Entwicklungsstand von Kessel und Rohrleitungswerkstoffen fűr hőhere Dampfzustande, VGB Konferenz “Kraftwerke im Wettbewerb-Technik, Betrieb und Umwelt” Kolonia, marzec 2003.

33. IEA, Carbon dioxide capture from power stations, 1992.

34. IEA Statistics - Electricity Information 2000.

35. Jabr R.A.: Robust Self-Scheduling Under Price Uncertainty Using Conditional Value-at-Risk, IEEE Transactions on Power Systems, November 2005, Vol. 20, No 4, pp.1852-1858, ISSN 0885-8950

36. Kalinowski T., Malko J., Szalbierz Z., Wilczyński A.: Efektywność międzynarodowego handlu energią elektryczną, Kaprint Lublin 1999, ISBN 83-905036-4-6

37. Kamrat W.: Metodologia oceny efektywności inwestowania na lokalnym rynku energii, Wydawnictwo Politechniki Gdańskiej, Gdańsk 1999, ISBN 83-88007-08-4

38. Kamrat W.: Metody oceny efektywności inwestowania, Rynek Energii, nr 6, 2002.

39. Kamrat W.: Ocena efektywności inwestowania w energetyce w warunkach rynkowych, mat. konf. XI Międzynarodowa Konferencja Naukowa „Aktualne Problemy w Elektroenergetyce” APE'2003, Gdańsk-Jurata, 11-13 czerwca 2003, Tom III , s.299-306, ISBN 83-909885-2-6

40. Kamrat W.: Ocena ryzyka przy realizacji inwestycji energetycznych, Wokół Energetyki, nr 5/2007, s.39-42

41. Karatzas I., Shreve S.E.: Brownian Motion and Stochastic Calculus, Springer-Verlag New York, Inc,. 1991, ISBN 0-387-97655-8, ISBN 3-540-97655-8.

42. Kijaer S., Thomsen F.: Stand der fortgeschrittenen űberkritischen fossilbefeurten Dampfkraftwerke im ELSAM-Bereich, VGB Kraftwerks Technik nr 6/1999 str.31-35.

43. Kocot H., Korab R.: Koszty zewnętrzne technologii elektroenergetycznych - metodyka wyznaczania, mat. konf. XIII Konferencji Naukowo-Technicznej Rynek Energii Elektrycznej REE'07, Kazimierz Dolny, 9-11 maja 2007 r., s.167-174

44. Kocot H., Korab R.: Ceny referencyjne dla wybranych technologii elektroenergetycznych, mat. konf. XIII Konferencji Naukowo-Technicznej Rynek Energii Elektrycznej REE'07, Kazimierz Dolny, 9-11 maja 2007 r., s.175-182

45. Kopecki K.: Ogólne założenia i metodyka rachunku gospodarczego w pracach planowo-projektowych w elektroenergetyce, PWN, Warszawa, 1960.

46. Kosiński J.: Nowe techniki w projektowaniu przedsięwzięć inwestycyjnych. Zastosowanie algorytmów genetycznych, Wydawca Instytut Organizacji i Zarządzania w Przemyśle „ORGMASZ”, Warszawa 2001.

47. Kotowicz J., Bartela Ł.: Energetyczne wykorzystanie biomasy drzewnej - przegląd technologii, Rynek Energii nr 6/2007

48. Kotowicz J., Janusz K.: Sposoby redukcji emisji CO₂ z procesów energetycznych, Rynek Energii, nr 1/2007

49. Kotowski W.: Elektrownie nowej generacji, Czysta Energia, październik 2007

50. Kozłowski M., Piesiewicz T., Weron A.: Zarządzanie ryzykiem ma rynku energii elektrycznej z uwzględnieniem segmentu bilansującego, giełdowego i pozagiełdowego, Energetyka, 12/2003

51. Krawczak M., Miklewski A., Jakubowski A., Konieczny P.: Zarządzanie ryzykiem inwestycyjnym. Wybrane zagadnienia., IBS PAN, Warszawa 2000

52. Kucowski J., Laudyn D., Przekwas M.: Energetyka a ochrona środowiska, WNT Warszawa 1997.

53. Kulikowski R., Libura M., Słomiński L.: Wspomaganie decyzji inwestycyjnych, IBS PAN, Warszawa 1998.

54. Кириллин В.А. и др.: Состяние и перспектива внедрения в энергетику МГД-установок, Теплоэнергетика 1986, No.2

55. Laudyn D., Pawlik M., Strzelczyk F.: Elektrownie, WNT, Warszawa 1997.

56. Laudyn D.: Rachunek ekonomiczny w elektroenergetyce, Oficyna Wydawnicza Politechniki Warszawskiej, Warszawa 1999, ISBN 83-7207-100-4

57. Malewicz W.: Wybrane problemy rachunku ekonomicznej efektywności inwestycji, Prace Naukowe Politechniki Szczecińskiej Nr 382 Instytut Elektrotechniki Nr 18, Szczecin 1988, ISSN 0208-7200

58. Malewicz W.: Wybrane problemy rachunku ekonomicznej efektywności inwestycji i postępu technicznego w gospodarce energetycznej, Prace Naukowe Politechniki Szczecińskiej Nr 488 Instytut Elektrotechniki Nr 24, Szczecin 1992, ISSN 0208-7200

59. Malko J., Wojciechowski H.: Przechwytywanie i magazynowanie CO₂ - technologie CCS, Wokół Energetyki, czerwiec 2007, s.15-19

60. McDonald R., Siegel D.: The Value of Waiting to Invest, Quarterly Journal of Economics, November 1986, Vol.101, pp.707-728

61. Mejro C.: Podstawy gospodarki energetycznej, WNT, Warszawa, 1980.

62. Metz, B., Davidson O., de Coninck H. C., Loos M., Meyer L.A. (eds.): IPCC special report on Carbon Dioxide Capture and Storage, Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, 2005

63. Modern Coal Based Power Plant Technology, niepublikowane materiały RWE, 2003.

64. Mory A., Tauschnitz J.: Mitverbrennung von Biomasse in Kohlekraftwerken, VGB Kraftwerks Technik 1/1999

65. Musiał K.: Porównanie technologii wytwarzania energii elektrycznej w Polsce, “Energoprojekt Katowice” S.A.

66. Musil L.: Die Gesamtplanung von Dampfkraftwerken, Springer Verlag, Berlin, 1958.

67. Naini A., Walden T., Pinno K., Stogran M., Mutysheva D.: Electricity Generation Technologies: Performance and Cost Characteristics, Canadian Energy Research Institute, August 2005.

68. Niewiedział E.: Analiza opłacalności układu kogeneracyjnego małej mocy pracującego na potrzeby drobnego odbiorcy indywidualnego, mat. konf. XII Międzynarodowa Konferencja Naukowa „Aktualne Problemy w Elektroenergetyce” APE'2005, Gdańsk-Jurata, 8-10 czerwca 2005, Tom III , s.73-80

69. Paska J.: Ekonomika w elektroenergetyce, Oficyna Wydawnicza Politechniki Warszawskiej, 2007.

70. Paska J.: Wytwarzanie energii elektrycznej, Oficyna Wydawnicza Politechniki Warszawskiej, 2005

71. Paska J.: Urządzenia bezpośredniej przemiany energii pierwotnej w elektryczną, Politechnika Warszawska, Instytut Elektroenergetyki

72. Piekarski B., Marciniak M.: Współspalanie i zgazowanie biomasy z wykorzystaniem technologii złoża fluidalnego, Komitet Problemów Energetyki PAN, Jabłonna, marzec 2003.

73. Popczyk J.: Innowacyjność technologiczna, odwołanie do własnych zasobów i konkurencja podstawą bezpieczeństwa dostaw energii dla odbiorców w Polsce w perspektywie 2020, mat. konf. XIII Konferencji Naukowo-Technicznej Rynek Energii Elektrycznej REE'07, Kazimierz Dolny, 9-11 maja 2007 r., s.15-42

74. Poradnik inżyniera elektryka, WNT, Warszawa 1997.

75. Rataj Z., Walewski A.W., Wojna W.B.: Badania oraz wariantowa analiza techniczna rozwiązań koncepcyjnych kotłów pyłowych na parametry nadkrytyczne z paleniskiem niskoemisyjnym - wybór technologii odsiarczania i odazotowywania spalin oraz utylizacji odpadów paleniskowych, Politechnika Śląska, UMIE, Gliwice, kwiecień 1998.

76. Roques F.A., Nuttall W.J., Newbery D.M.: Using Probabilistic Analysis to Value Power Generation Investments under Uncertainty, CWPE 0650 and EPRG 065, Electricity Policy Research Group, University of Cambridge, England, July 2006.

77. Rothwell G.S.: Electric Utility Power Plant Choice Under Investment Regulation, Ph.D. dissertation, Department of Economics, University of California, Berkeley, 1985.

78. Rothwell G.S., Gomez T.: Electricity Economics: Regulation and Deregulation, IEEE Press, 2002.

79. Rothwell G.S., Sowiński J.: Analiza możliwych opcji modelu decyzyjnego planowania inwestycji w elektroenergetyce, mat. konf. V Konferencji Naukowo-Technicznej Rynek Energii Elektrycznej: Rynek Hurtowy, Rynki Lokalne REE'98, Nałęczów, 14-15 maja 1998 r., s.297-304.

80. Salazar H., Liu Ch., Chu R.F.: Decision Analysis of Merchant Transmission Investment by Perpetual Options Theory, IEEE Transactions on Power Systems, Vol. 22, No. 3, August 2007, pp. 1194-1201

81. Shahidehpour M., Yamin H., Li Z.: Market Operations in Electric Power Systems: Forecasting, Scheduling, and Risk Assessment, New York: Wiley, 2002

82. Simbeck D.R., Johnson H.E.: Report on SFA Pacific Gasification Databases and World Market Report, 1999 Gasification Technologies Conference, San Francisco, October 1999.

83. Skorek J.; Ocena efektywności energetycznej i ekonomicznej gazowych układów kogeneracyjnych małej mocy, monografia, Wydawnictwo Politechniki Śląskiej, Gliwice 2002.

84. Skorek J., Kalina J.: Gazowe układy kogeneracyjne, WNT, Warszawa 2005.

85. Skorek J., Kalina J., Bartnik R., Sawicki W.: Analiza techniczno-ekonomiczna opłacalności nadbudowy węglowej elektrociepłowni parowej turbiną gazową i kotłem odzyskowym, Energetyka, nr 4(574)/2002, s.195-201

86. Smith J.W.: Supercritical (Once Through) Boiler Technology, Babcock&Wilcom Company, nr BR-1658, May 1998.

87. Smith J.: IGCC Technology Continues to Develop, Power Engineering, 11/2003

88. SVC Schwarze Pumpe, serwis internetowy.

89. The Royal Academy of Engineering: The Costs of Generating Electricity, March 2004, ISBN 1-903496-11-X

90. The ZECA Process: „Zero Emission” Hydrogen and/or Electricity from Coal and Carbon Fuels, An overview of the technology, ZECA Corporation, September 2002.

91. Tilman D.: Cofiring Biomass in Coal-Fired Boilers, Foster Wheeler Review, Spring 1999, Volume 1, No. 1.

92. Tolley G.S., Jones D.W. i in.: The Economic Future of Nuclear Power, The University of Chicago, August 2004.

93. U.S. Department of Energy (DOE), serwis internetowy.

94. Veenhuizeen D.: Karita P800 supercritical 360 MWe PFBC plant reaches full power, Modern Power Systems, November 1999, s.35-37.

95. Weron A., Weron R.: Giełda energii. Strategie zarządzania ryzykiem, Wydawca CIRE, Wrocław 2000.

96. Zaporowski B.: Efektywność energetyczna i ekonomiczna skojarzonego wytwarzania energii elektrycznej i ciepła w elektrociepłowniach opalanych gazem ziemnym, Polityka Energetyczna, Tom 8, PAN, Kraków 2005, s. 115-130, PL ISSN 1429-6675

97. Zaporowski B., Szczerbowski R., Wróblewski R.: Analiza efektywności energetycznej i ekonomicznej elektrociepłowni małej mocy opalanych biomasą, Polityka Energetyczna, Tom 10, PAN, Kraków 2007, s. 367-378, PL ISSN 1429-6675

[98] Integrated pollution prevention and control (IPPC), Reference document on best available techniques for large combustion plants, May 2005

[99] Commission of the European Communities, An Energy Policy for Europe, Brussels, 10.1.2007, COM(2007)

W dalszej części pracy w modelach, w których w sposób jawny nie uwzględnia się kosztów wytwarzania energii elektrycznej, symbol P oznacza przychód, rozumiany jako różnica wpływów ze sprzedaży energii elektrycznej i kosztów jej wytwarzania, przyjętych jako suma kosztów prowadzenia ruchu, remontów i paliwa. W przypadku uwzględniania kosztów wytwarzania energii elektrycznej symbol P oznacza wpływy ze sprzedaży energii elektrycznej, wyznaczone jako iloczyn ceny na hurtowym rynku energii HRE i ilości sprzedanej energii elektrycznej.

- 1 -

---