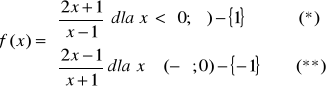SYLLABUS

z matematyki

2002 -2005

WARSZAWA 2000

Publikację przygotowały Okręgowe Komisje Egzaminacyjne w Gdańsku, Jaworznie, Krakowie, Łodzi, Łomży, Poznaniu, Warszawie, Wrocławiu.

Prace koordynowała Okręgowa Komisja Egzaminacyjna w Warszawie w porozumieniu z Centralną Komisją Egzaminacyjną w Warszawie.

ISBN 83-88564-51-X

spis treści

Przedmowa

• Arkusz egzaminacyjny I - poziom podstawowy - wersja A

• Arkusz egzaminacyjny I - poziom podstawowy - wersja B

• Arkusz egzaminacyjny II - poziom rozszerzony

PRZEDMOWA

W literaturze dydaktycznej ostatniego dwudziestolecia dominuje przeświadczenie, że matematyka służy rozwijaniu kwalifikacji i kompetencji intelektualnych, które uznajemy dziś za konieczne elementy wykształcenia ogólnego, potrzebnego współczesnemu człowiekowi, niezależnie od dziedziny jego działalności.

Człowiek, zajmując się matematyką, rozwija swoją osobowość, uczy się wytrwałości w pokonywaniu trudności, rzetelności i systematyczności w działaniu, kształtuje umiejętność prezentowania swoich racji precyzyjnym językiem. Ponadto uczy się przyjmować logiczną argumentację rozmówcy, dokonywać krytycznej analizy tekstu własnego i cudzego, dostrzegania własnych błędów.

Postęp cywilizacyjny sprawił, że matematyka stała się niezbędna, aby racjonalnie funkcjonować w życiu codziennym: szybko i trafnie interpretować informacje, podejmować korzystne decyzje, kierować się obiektywnymi racjami. Matematyka jest obecna w wielu dziedzinach działalności człowieka, niezbędna w wykonywaniu wielu zawodów, stąd kto zna matematykę, ten ma większe szanse na awans zawodowy.

Przywrócenie matematyki na egzaminie maturalnym jako przedmiotu obowiązkowego podniesie jej rangę w szkole, a w konsekwencji będzie sprzyjać łatwiejszemu odnalezieniu się młodego człowieka w dorosłym życiu.

wstęp

Szanowni Państwo,

w 2002 roku maturzyści przystąpią po raz pierwszy do zewnętrznie organizowanego i przeprowadzanego egzaminu maturalnego. Wobec różnorodności programów szkolnych i podręczników nowa matura odwołuje się do tego, co wspólne w edukacji polskich uczniów i co zostało określone w Podstawie programowej kształcenia ogólnego, a ukonkretnione w Standardach wymagań egzaminacyjnych opracowanych przez Centralną Komisję Egzaminacyjną.

Celem egzaminu maturalnego jest ocena poziomu wykształcenia ogólnego. Matura przeprowadzona według jednakowych, obowiązujących w całym kraju standardów, umożliwi zobiektywizowaną i porównywalną ocenę osiągnięć zdających. Ma szansę stać się egzaminem obiektywnym, rzetelnym i trafnym, dającym wiarygodną informację maturzystom, ich rodzicom, szkołom, a także uczelniom i pracodawcom.

Wraz z ogłoszeniem w sierpniu 1998 roku przez Ministra Edukacji Narodowej decyzji o wprowadzeniu od maja 2002 roku systemu oceniania zewnętrznego, rozpoczęły się prace nad zasadami jego funkcjonowania i określeniem wymagań egzaminacyjnych. W lutym 2000 roku zostały ogłoszone Standardy wymagań egzaminacyjnych, a obecnie dociera do rąk Państwa informator, tradycyjnie zwany syllabusem, opisujący wymagania, formę egzaminu i zasady jego przeprowadzania. W zeszycie tym zamieszczono również przykładowe arkusze egzaminacyjne i arkusze rozwiązane przez uczniów klas czwartych przygotowujących się w tym roku do matury. Informatory zostały opracowane oddzielnie dla każdego przedmiotu egzaminacyjnego. Aby ułatwić czytelnikom korzystanie z nich, nadano im taki sam układ.

Najważniejszym zadaniem informatora jest pomoc uczniom przygotowującym się do czekającego ich egzaminu maturalnego.

Egzamin maturalny, poczynając od 2002 roku będzie inny niż obecnie. Wynika to z konieczności dostosowania matury do potrzeb zmieniających się wymagań, stawianych przez rynek pracy i wyższe uczelnie absolwentom szkół średnich. Nowy egzamin maturalny będzie sprawdzać nie tylko to, co zdający umie, ale również jak potrafi pracować nad dostarczoną informacją, tekstem czy ilustracją. Przy lawinowo rosnącej wiedzy, coraz istotniejsza staje się umiejętność jej wykorzystania, przetworzenia, wyciągnięcia właściwych wniosków, przeprowadzenie porównań, sporządzenie syntezy czy analizy posiadanych danych, a nie tylko jej pamięciowe opanowanie i odtworzenie w odpowiednim porządku, dlatego też zmienia się forma wszystkich egzaminów. Z żadnego przedmiotu nie będzie kilkugodzinnego wypracowania. Zostaną one zastąpione krótszymi formami, sprawdzającymi różne elementy wiedzy i umiejętności w czasie zbliżonym do dotychczas obowiązującego.

Nie tylko forma egzaminu została zmieniona. Istotną nowością jest wprowadzenie obowiązkowych przedmiotów maturalnych. Przedmiotów, które są niezbędne w komunikacji we współczesnym świecie. Pierwszym jest język ojczysty, którego bardzo dobra znajomość będzie jeszcze istotniejsza niż obecnie, wraz z wejściem do wspólnoty europejskiej. Następnym przedmiotem obowiązkowym będzie język obcy nowożytny, bez znajomości którego funkcjonowanie we współczesnym świecie staje się coraz bardziej utrudnione. Trzecim obowiązkowym przedmiotem jest matematyka, uniwersalny język, bez którego znajomości nie sposób poruszać się w życiu codziennym - w banku, w sklepie, pisząc zeznanie podatkowe czy obliczając odpisy na ubezpieczenie.

Inną nowością będzie wprowadzenie dwóch poziomów egzaminów obowiązkowych. Każdy ze zdających musi zdać wymienione trzy przedmioty na poziomie podstawowym. Kto jest szczególnie zainteresowany danym przedmiotem lub opanował komunikację językową w stopniu wyższym, będzie mógł zdawać egzamin z przedmiotów obowiązkowych na poziomie rozszerzonym i zostanie to odnotowane na świadectwie maturalnym.

Oprócz przedmiotów obowiązkowych, każdy zdający będzie musiał zdać egzamin z wybranego przedmiotu. Jeżeli zdecyduje się zdawać więcej niż jeden przedmiot wybrany też będzie to możliwe.

Następną nowością będzie zmiana kolejności i sposobu zdawania egzaminu. Jako pierwsze będą zdawane egzaminy ustne, wyłącznie z języka ojczystego i języków obcych nowożytnych. Dopiero w drugiej kolejności będą zdawane egzaminy pisemne z języków i z pozostałych przedmiotów, z których egzaminów ustnych już się nie przewiduje.

Ostatnią zmianą, chyba najważniejszą, jest wprowadzenie jasnego opisu wymagań i jednolitych kryteriów oceniania prac maturalnych wszystkich zdających w całym kraju. Pozwoli to uczniom na lepsze przygotowanie się do egzaminu, a egzaminatorom na zobiektywizowanie stawianych ocen, natomiast wyższym uczelniom umożliwi rozważenie rezygnacji z powtarzania egzaminów z poszczególnych przedmiotów oraz wykorzystania wyników egzaminów maturalnych jako podstawy do rekrutacji kandydatów na wyższe uczelnie. Oczywiście, będzie to narzucało konieczność wyboru na maturze takich przedmiotów, jakie wskaże uczelnia lub wydział, na który będą chcieli kandydować. Mamy nadzieję, że syllabus, który obecnie Państwo otrzymują spełni wszystkie pokładane w nim nadzieje i przyczyni się do zdania przez wszystkich egzaminu maturalnego.

Życzymy powodzenia!

I. PODSTAWY PRAWNE EGZAMINU

1. akty prawne

• Ustawa z dnia 7 września 1991 r. o systemie oświaty z późniejszymi zmianami (Dz. U. z 1996 r. Nr 67, poz. 329 i Nr 106, poz. 496 z 1997 r., Nr 28, poz. 153 i Nr 141, poz. 943 i z 1998 r. Nr 117, poz. 759 i Nr 162, poz. 1126 oraz z 2000 r. Nr 12, poz. 136).

• Rozporządzenie Ministra Edukacji Narodowej z dnia 15 lutego 1999 r. w sprawie podstawy programowej kształcenia ogólnego (Dz. U. z 1999 r. Nr 14, poz. 129).

• Rozporządzenie Ministra Edukacji Narodowej z dnia 19 kwietnia 1999 r. w sprawie zasad oceniania, klasyfikowania i promowania uczniów i słuchaczy oraz przeprowadzania egzaminów i sprawdzianów w szkołach publicznych (Dz. U. z 2000 r. Nr 6, poz. 72).

• Rozporządzenie Ministra Edukacji Narodowej z dnia 21 lutego 2000 r. w sprawie standardów wymagań będących podstawą przeprowadzania sprawdzianów i egzaminów (Dz. U. z 2000 r. Nr 17, poz. 215).

• Warunki zdawania egzaminu maturalnego dla młodzieży o specjalnych potrzebach edukacyjnych zostaną określone przez Ministra Edukacji Narodowej odrębnymi przepisami.

2. podstawa programowa matematyki

Cele edukacyjne

1. Zdobycie przez uczniów umiejętności operowania podstawowymi pojęciami matematycznymi.

2. Dostrzeganie, formułowanie i rozwiązywanie przez uczniów prostych problemów teoretycznych.

3. Rozwijanie umiejętności logicznego rozumowania i wnioskowania.

4. Przygotowanie uczniów do wykorzystania wiedzy matematycznej przy rozwiązywaniu problemów z różnych dziedzin.

Zadania szkoły

1. Kształtowanie umiejętności operowania przez uczniów podstawowymi obiektami matematycznymi.

2. Kształcenie umiejętności przydatnych w życiu codziennym (obliczanie prawdopodobieństwa, odczytywanie informacji z tabel, wykresów i diagramów).

3. Przedstawianie zadań stymulujących dostrzeganie, formułowanie i rozwiązywanie przez uczniów prostych problemów teoretycznych.

4. Rozwijanie umiejętności precyzyjnego formułowania myśli przez uczniów.

5. Kształtowanie wyobraźni geometrycznej uczniów.

6. Rozwijanie umiejętności logicznego rozumowania i wnioskowania (definiowanie podstawowych obiektów matematycznych, klasyfikowanie tych obiektów, podawanie przykładów i kontrprzykładów, przeprowadzanie prostych rozumowań dedukcyjnych).

Treści

1. Liczby, równania i funkcje:

• usystematyzowanie wiadomości o liczbach wymiernych;

• przykłady liczb niewymiernych; przybliżenia dziesiętne liczb rzeczywistych;

• obliczenia procentowe;

• potęgowanie liczb rzeczywistych (potęga o wykładniku całkowitym, potęga o wykładniku wymiernym);

• pojęcie funkcji;

• przykłady wykresów funkcji liczbowych; przekształcanie wykresów;

• odczytywanie własności funkcji z wykresu;

• funkcja liniowa;

• funkcja kwadratowa;

• równania i nierówności liniowe z jedną niewiadomą;

• równania i nierówności liniowe z dwiema niewiadomymi; układy równań liniowych i ich interpretacja geometryczna;

• równania i nierówności kwadratowe z jedną niewiadomą i ich interpretacja geometryczna;

• przykłady prostych równań i nierówności trzeciego stopnia;

• proporcjonalność prosta i odwrotna; wykres proporcjonalności odwrotnej;

• nierówności typu
  .

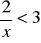
2. Ciągi liczbowe:

• przykłady ciągów liczbowych (w tym ciągów rekurencyjnych);

• własności ciągu;

• ciąg arytmetyczny i ciąg geometryczny; suma wyrazów ciągu arytmetycznego, suma wyrazów ciągu geometrycznego;

• procent składany;

• szereg geometryczny.

3. Elementy rachunku prawdopodobieństwa:

• elementy kombinatoryki;

• prawdopodobieństwo i jego związek z częstością;

• przykłady obliczania prawdopodobieństwa;

• przykłady praktycznego zastosowania statystyki (odczytywanie tabel, diagramów i wykresów, przedstawianie danych empirycznych w postaci diagramów i wykresów).

4. Geometria:

• usystematyzowanie wiadomości o figurach płaskich;

• kąty i wielokąty; okręgi i koła; obwody i pola wielokątów i kół;

• odległość na płaszczyźnie;

• przykłady izometrii płaszczyzny (przesunięcie, symetria osiowa, symetria środkowa);

• przystawanie figur;

• wektory i ich zastosowania;

• twierdzenie Pitagorasa i twierdzenie Talesa;

• jednokładność;

• podobieństwo figur;

• konstrukcje geometryczne;

• funkcje trygonometryczne; podstawowe tożsamości trygonometryczne; najprostsze zastosowania funkcji trygonometrycznych (twierdzenie sinusów, twierdzenie kosinusów);

• prostopadłość i równoległość w przestrzeni;

• kąt nachylenia prostej do płaszczyzny;

• kąt dwuścienny;

• usystematyzowanie wiadomości o wielościanach i bryłach obrotowych;

• przekroje płaskie wielościanów i brył obrotowych;

• pola powierzchni i objętości wielościanów i brył obrotowych.

Osiągnięcia

1. Operowanie podstawowymi obiektami matematycznymi.

2. Przeprowadzanie prostych rozumowań dedukcyjnych.

3. Zdobycie umiejętności przydatnych w życiu codziennym (obliczanie prawdopodobieństwa, odczytywanie informacji z tabel, wykresów i diagramów).

4. Precyzyjne formułowanie myśli.

3. standardy wymagań egzaminacyjnych

Egzamin maturalny sprawdza wiadomości i umiejętności pozwalające zdającemu:

1. wykazać się znajomością i rozumieniem:

Poziom podstawowy	Poziom rozszerzony
wskazanych pojęć, np. rozwiązania równania, funkcje oraz tych ich własności, które są konieczne do rozumienia wykonywanych obliczeń, własności funkcji, elementów geometrii i rachunku prawdopodobieństwa, wskazanych algorytmów, np. rozwiązalności równania kwadratowego, wyznaczania n-tego wyrazu ciągu geometrycznego oraz typowych sytuacji, w których można się nimi posłużyć.	jak na poziomie podstawowym, jak na poziomie podstawowym, wskazanych pojęć, np. logarytmu, pochodnej funkcji, twierdzeń dotyczących np. monotoniczności funkcji logarytmicznej, sinusów, związku pochodnej z monotonicznością funkcji oraz ich interpretacji w konkretnych sytuacjach.

2. stosować posiadaną wiedzę do rozwiązywania zadań teoretycznych i praktycznych, czyli:

Poziom podstawowy

Poziom rozszerzony

posłużyć się znaną definicją, np. figur jednokładnych, twierdzeniem, np. o stosunku pól figur jednokładnych w typowej sytuacji, rozwiązywać zadania wymagające przeprowadzenia analogicznego rozumowania wg podanego schematu, odczytywać informacje ilościowe, np. dotyczące argumentów i wartości funkcji oraz proste informacje jakościowe, np. dotyczące własności funkcji z tabel, diagramów i wykresów, posługiwać się miarą, np. długości, pola i objętości oraz przybliżeniami dziesiętnymi tych miar w prostych sytuacjach z życia codziennego.

jak na poziomie podstawowym, jak na poziomie podstawowym, jak na poziomie podstawowym, jak na poziomie podstawowym, formułować proste zależności, np. rekurencyjnie, wyciągać wnioski z podanych zależności, np. typu funkcyjnego, wyrażonych równaniem, uzasadniać prawdziwość wniosków.

3. stosować metody matematyczne w sytuacjach problemowych, czyli:

Poziom podstawowy

Poziom rozszerzony

podać opis matematyczny w postaci wyrażenia algebraicznego, funkcji, równania, nierówności, przekształcenia geometrycznego do podanej sytuacji (także praktycznej), i wykorzystać go do rozwiązania problemu, dobrać odpowiedni algorytm do wskazanej sytuacji problemowej i ocenić przydatność uzyskanych wyników w typowej sytuacji, przetworzyć informacje wyrażone w postaci wyrażenia algebraicznego, równania, wzoru lub wykresu funkcji, opisu wektorowego na inną formę ułatwiającą rozwiązanie problemu.

jak na poziomie podstawowym, jak na poziomie podstawowym, jak na poziomie podstawowym, interpretować jakościowo informacje z tabel, diagramów, wykresów oraz ustalać i formułować między nimi proste zależności, wykorzystywać je w toku badania typowej sytuacji problemowej, stosować definicje i twierdzenia w rozwiązywaniu problemów.

4. rozwiązywać zadania wymagające argumentowania i prowadzenia rozumowań typu matematycznego, czyli:

Poziom podstawowy	Poziom rozszerzony
interpretować treść zadania, zapisywać warunki i zależności między obiektami, dobierać i zastosować odpowiednie definicje, twierdzenia, własności i algorytmy, analizować otrzymane wyniki, argumentować i uzasadniać wnioski oraz opisywać je w sposób czytelny i poprawny językowo.	jak na poziomie podstawowym, jak na poziomie podstawowym, przeprowadzić i zredagować pełny dowód twierdzenia.

II. Matura 2002 w pytaniach uczniów

Jakie są podstawowe zasady egzaminu maturalnego w roku 2002?	Egzamin maturalny komisyjnie sprawdza poziom wykształcenia ogólnego zdających z zakresu przedmiotów określonych Standardami wymagań egzaminacyjnych. Do egzaminu maturalnego mogą przystąpić absolwenci szkół ponadpodstawowych posiadający świadectwo ukończenia szkoły, dającej prawo zdawania egzaminu maturalnego. Egzamin jest obowiązkowy dla kandydatów na studia wyższe. Postępowanie egzaminacyjne rozpoczyna opublikowanie syllabusa a kończy wydanie świadectwa dojrzałości. Harmonogram postępowania egzaminacyjnego ustala Centralna Komisja Egzaminacyjna (CKE). Egzamin będzie organizowany dwa razy w roku: w maju - po zakończeniu zajęć w programowo najwyższej klasie szkół, dających uprawnienia do przystąpienia do egzaminu maturalnego, począwszy od maja 2002 r. - i w styczniu - począwszy od stycznia roku 2003. Egzamin składa się z części wewnętrznej - ustnej i z części zewnętrznej - pisemnej.
Z jakich przedmiotów trzeba i można zdawać maturę?	Egzamin zdawany jest obowiązkowo z czterech przedmiotów: języka polskiego - w części wewnętrznej i zewnętrznej, języka obcego nowożytnego - w części wewnętrznej i zewnętrznej, matematyki - w części zewnętrznej, przedmiotu wybranego przez ucznia - w części zewnętrznej, z wyjątkiem innego niż obowiązkowy języka obcego nowożytnego, który jest zdawany w części wewnętrznej i zewnętrznej. Zdający z grup mniejszości narodowych zdają obowiązkowo przedmioty wymienione w punkcie 1 oraz język ojczysty danej mniejszości narodowej. Zdający ma prawo wybrać dodatkowo więcej niż jeden przedmiot. Nie ma to wpływu na liczbę i wybór przedmiotów zdawanych obowiązkowo.
Na jakim poziomie będzie można zdawać poszczególne przedmioty?	Egzamin z przedmiotów obowiązkowych - języka polskiego, języka ojczystego mniejszości narodowej, języka obcego nowożytnego i matematyki - może być zdawany na dwóch poziomach - podstawowym lub rozszerzonym. Rozróżnienie poziomów egzaminu z języka polskiego, języka ojczystego mniejszości narodowej i matematyki wprowadza się w części pisemnej egzaminu, a z języka obcego nowożytnego w części ustnej i pisemnej. Absolwent klasy z językiem obcym wykładowym lub klasy dwujęzycznej uzyskuje na świadectwie adnotację o ukończeniu tego typu klasy, jeżeli zda egzamin z danego języka według specjalnie przygotowanych arkuszy egzaminacyjnych dla absolwentów tego typu szkół oraz przedmioty dodatkowe według zasad określonych w dwustronnych porozumieniach międzynarodowych. Inny, niż zdawany jako obowiązkowy, język obcy nowożytny jako przedmiot wybrany, zdawany jest, w części ustnej i pisemnej, na jednym poziomie zawierającym zadania z poziomu podstawowego i rozszerzonego.
Kiedy należy wybrać przedmiot i poziom zdawania przedmiotu na egzaminie?	Zdający deklaruje, na początku ostatniego roku nauki w szkole dającej uprawnienia do przystąpienia do egzaminu maturalnego zgodnie z procedurą obowiązującą w okręgowej komisji egzaminacyjnej, wybór: przedmiotu (przedmiotów) na egzamin, poziomu egzaminu z przedmiotów obowiązkowych, okresu z historii, typu komputera, środowiska komputerowego i programów komputerowych z informatyki, tematu z języka obcego nowożytnego na poziomie rozszerzonym, tematu z języka polskiego, języka ojczystego mniejszości narodowej na część wewnętrzną egzaminu z list tematów, przygotowanych przez nauczycieli danego przedmiotu w szkole. Wybór przedmiotu (przedmiotów) na egzamin nie zależy od profilu nauczania szkoły (oddziału), do której uczęszczał absolwent, ani od języków nauczanych w  szkole. W przypadku braku w szkole egzaminatora z wybranego przedmiotu zdający zostanie skierowany na egzamin do innej szkoły. W wyjątkowych, szczególnie uzasadnionych przypadkach, jednak nie później niż cztery miesiące przed terminem egzaminu maturalnego, zdający może dokonać zmian w deklarowanych wyborach z zastrzeżeniem, że w przypadku języka ojczystego wszelkie czynności związane z wyborem i doprecyzowaniem tematu kończy pierwsza konsultacja, która powinna się odbyć najpóźniej 31 października. Zdający nie może w trakcie egzaminu zmieniać wybranego okresu z historii i środowiska komputerowego z informatyki. Zdający może w trakcie egzaminu zrezygnować ze zdawania egzaminu na poziomie rozszerzonym.
Jaka będzie matura uczniów szkół z ojczystym językiem mniejszości narodowych i uczniów szkół dwujęzycznych?	Absolwenci szkół lub oddziałów z ojczystym językiem nauczania mniejszości narodowych i grup etnicznych oraz absolwenci szkół dwujęzycznych mogą zdawać na egzaminie przedmiot lub przedmioty w języku polskim lub odpowiednio w języku danej mniejszości narodowej lub grupy etnicznej albo w danym języku obcym. Wyboru języka, w którym będzie zdawany przedmiot, absolwent dokonuje wraz z deklaracją wyboru przedmiotu, o której mowa w pytaniu D.
Gdzie można zdawać maturę?	Część zewnętrzną egzaminu organizuje i przeprowadza komisja okręgowa w wyznaczonych szkołach lub placówkach, posiadających odpowiednie warunki lokalowe i techniczne zapewniające prawidłowy przebieg egzaminu. Zdający, którzy ukończyli szkołę w latach poprzednich lub wyrazili wolę zdawania egzaminu w szkole innej niż ukończona, są kierowani do szkoły wyznaczonej przez komisję okręgową.
Jakie warunki muszą być zapewnione na sali egzaminacyjnej?	Pomieszczenie szkolne, w którym jest przeprowadzany egzamin, musi spełniać warunki określone w przepisach BHP. Odległość między piszącymi nie może być mniejsza niż 1,5 metra z każdej strony. Przy stoliku może siedzieć wyłącznie jeden zdający. Na stolikach w trakcie pisania mogą znajdować się jedynie przybory pomocnicze dopuszczone przez syllabus danego przedmiotu oraz arkusze egzaminacyjne. Zdający chory lub niepełnosprawny w trakcie egzaminu może mieć na stoliku leki i inne pomoce medyczne przepisane przez lekarza lub konieczne ze względu na chorobę lub niepełnosprawność Posiłki dla zdających i egzaminatorów mogą być dostępne jedynie na zewnątrz sali egzaminacyjnej poza czasem przeznaczonym na egzamin, z wyjątkiem przypadków, o których mowa w punkcie 5.
Jak powinien być zorganizowany egzamin?	W skład zespołu nadzorującego przebieg egzaminu w danym pomieszczeniu wchodzi co najmniej trzech nauczycieli. Przewodniczącym zespołu nadzorującego przebieg egzaminu może być jedynie nauczyciel wpisany do ewidencji egzaminatorów. Co najmniej jeden członek zespołu powinien być zatrudniony w innej szkole. W skład zespołu nie mogą wchodzić nauczyciele danego przedmiotu oraz wychowawca klasy zdających. Egzamin pisemny przebiega zgodnie z harmonogramem określonym przez CKE. Szczegóły przebiegu egzaminu określa każdorazowo instrukcja zawarta w arkuszu egzaminacyjnym. Czas egzaminu liczy się od przekazania zdającym arkuszy egzaminacyjnych. W czasie egzaminu pisemnego w sali egzaminacyjnej przebywają co najmniej trzej członkowie zespołu, w tym jeden pełniący funkcję przewodniczącego. W czasie egzaminu zdający nie powinni opuszczać sali egzaminacyjnej. Przewodniczący zespołu może zezwolić na opuszczenie sali, po zapewnieniu warunków wykluczających możliwość kontaktowania się zdającego z innymi osobami, z wyjątkiem osób udzielających pomocy medycznej. Członkom zespołu nadzorującego przebieg egzaminu nie wolno udzielać żadnych wyjaśnień, komentarzy dotyczących zadań egzaminacyjnych. W przypadku stwierdzenia niesamodzielnego rozwiązywania zadań egzaminacyjnych, przewodniczący zespołu lub dyrektor okręgowej komisji egzaminacyjnej unieważnia egzaminy ze wszystkich przedmiotów danego zdającego. Do sali egzaminacyjnej można wnosić jedynie materiały i środki dydaktyczne określone w syllabusie. Arkusze egzaminacyjne są zbierane po zakończeniu każdej części egzaminu.
Ile dni trwa egzamin?	Egzamin zewnętrzny z danego przedmiotu odbywa się jednego dnia i polega na rozwiązaniu zadań zawartych w arkuszach egzaminacyjnych, odrębnych dla każdej części egzaminu. Między poszczególnymi częściami egzaminu następować będą przerwy.
Jak sprawdzane są prace?	Poszczególne arkusze egzaminacyjne, z każdej części egzaminu z danego przedmiotu, są sprawdzane i oceniane przez różnych egzaminatorów zewnętrznych, przeszkolonych przez okręgowe komisje egzaminacyjne i wpisanych do rejestru CKE. Wynik egzaminu jest wyrażony w procentach. Negatywny wynik egzaminu z wybranego dodatkowo przedmiotu, o którym mowa w  pyt. B pkt 3, nie ma wpływu na końcowy wynik egzaminu i nie odnotowuje się go na świadectwie dojrzałości. Komisja okręgowa ustala listę osób, które zdały egzamin.
Czy można powtarzać niezdany egzamin ?	Absolwent, który nie zdał egzaminu z określonego przedmiotu, może przystąpić ponownie do egzaminu z tego przedmiotu w kolejnych sesjach egzaminacyjnych, przez okres pięciu lat. Po upływie pięciu lat od daty pierwszego egzaminu absolwent, o którym mowa w pkt 1, zdaje powtórny egzamin w pełnym zakresie. Przy powtórnym egzaminie z przedmiotu wybranego absolwent może wybrać inny przedmiot, z zachowaniem przepisu zapisanego w pyt. D pkt 1.
Czy można poprawiać wynik uzyskany na egzaminie?	Absolwent, który chce podwyższyć wynik egzaminu w części zewnętrznej z jednego lub kilku przedmiotów, ma prawo przystąpić ponownie do egzaminu w kolejnej sesji.
Kiedy można powtórnie przystąpić do egzaminu, jeśli został on przerwany?	Absolwent, który nie przystąpił do egzaminu lub przerwał egzamin, ma prawo przystąpić do egzaminu w kolejnych sesjach egzaminacyjnych, w styczniu lub w maju każdego roku.
Kto może być zwolniony z egzaminu?	Laureaci olimpiad przedmiotowych są zwolnieni z egzaminu z danego przedmiotu, na zasadach określonych w przepisach w sprawie organizacji konkursów i olimpiad przedmiotowych. Laureatom olimpiad uprawnienia wymienione w punkcie 1 przysługują także wtedy, gdy przedmiot nie był objęty szkolnym planem nauczania danej szkoły. Zwolnienie z egzaminu z danego przedmiotu jest równoznaczne z uzyskaniem z tego przedmiotu najwyższego wyniku, a w przypadku przedmiotów obowiązkowych - równoznaczne z uzyskaniem najwyższego wyniku na poziomie rozszerzonym.
Na jakich zasadach zdają egzamin absolwenci niepełnosprawni?	Absolwenci niepełnosprawni lub niesprawni czasowo przystępują do egzaminu w powszechnie obowiązujących terminach i według obowiązujących wymagań egzaminacyjnych, przy kryteriach dostosowanych do rodzaju niepełnosprawności. Komisja okręgowa zobowiązana jest do sprawdzenia czy zostały zapewnione warunki i formy przeprowadzania egzaminu odpowiednie do możliwości zdających o specjalnych potrzebach edukacyjnych
W jakich sytuacjach można złożyć odwołanie od egzaminu?	Jeżeli w trakcie wewnętrznej części egzaminu nie były przestrzegane przepisy dotyczące przebiegu egzaminu, absolwent może w terminie dwóch dni od zaistnienia nieprawidłowości złożyć odwołanie do przewodniczącego zespołu szkolnego. Przewodniczący zespołu szkolnego rozpatruje odwołanie w terminie trzech dni od jego otrzymania. Od rozstrzygnięcia przewodniczącego zespołu szkolnego absolwent może odwołać się do dyrektora komisji okręgowej w terminie trzech dni od otrzymania rozstrzygnięcia. Dyrektor komisji okręgowej rozpatruje odwołanie w terminie czternastu dni od jego otrzymania. Rozstrzygnięcie dyrektora komisji okręgowej jest ostateczne. Jeżeli w trakcie zewnętrznej części egzaminu nie były przestrzegane przepisy dotyczące przebiegu egzaminu absolwent może w terminie dwóch dni roboczych od dnia egzaminu złożyć odwołanie do dyrektora komisji okręgowej. Dyrektor komisji okręgowej rozpatruje odwołanie w terminie pięciu dni roboczych od jego otrzymania. Od rozstrzygnięcia dyrektora komisji okręgowej absolwent może odwołać się do dyrektora Komisji Centralnej, w terminie siedmiu dni roboczych od jego otrzymania. Dyrektor Komisji Centralnej rozpatruje odwołanie w terminie siedmiu dni roboczych od jego otrzymania. Rozstrzygnięcie dyrektora Komisji Centralnej jest ostateczne.

III. CELE EGZAMINU MATURALNEGO

Egzamin maturalny z matematyki sprawdza nie tylko odtwarzanie ale i rozumienie wiadomości, umiejętność zastosowania ich w sytuacjach typowych i problemowych, precyzyjnego formułowania myśli, operowania podstawowymi obiektami matematycznymi, przeprowadzania prostych rozumowań dedukcyjnych oraz posługiwania się metodami matematycznymi w rozwiązywaniu zadań, a także umiejętność odczytywania, interpretowania i przetwarzania informacji.

Celem egzaminu maturalnego z matematyki jest:

1. Ocena poziomu wiedzy i umiejętności absolwenta, czyli stopnia opanowania wymagań egzaminacyjnych w zakresie określonym w Podstawie programowej i Standardach wymagań egzaminacyjnych.

2. Poinformowanie rodziców, nauczycieli, władz oświatowych i samorządowych, wyższych uczelni i pracodawców o poziomie wiedzy i umiejętności absolwentów, aby umożliwić:

• prognozowanie na podstawie wyników egzaminów przygotowania absolwentów do dalszego kształcenia,

• diagnozowanie pracy szkół i określanie czynników sprzyjających podnoszeniu poziomu kształcenia,

• motywowanie nauczycieli władz oświatowych i samorządowych do sprawdzania jakości nauczania matematyki w szkołach.

IV. STRUKTURA I FORMA EGZAMINU

1. Egzamin maturalny z matematyki jest egzaminem zewnętrznym i ma formę pisemną.

2. Egzamin zdawany jest na poziomie podstawowym (obowiązkowym) lub rozszerzonym.

3. Egzamin trwa 4,5 godziny zegarowej i składa się z dwóch części:

część pierwsza egzaminu trwa 120 minut	część egzaminu wspólna dla obu poziomów
część druga egzaminu trwa 150 minut	część egzaminu wyłącznie dla poziomu rozszerzonego

4. Uczniowie, którzy zadeklarowali zdawanie egzaminu na poziomie rozszerzonym, do drugiej części egzaminu przystępują po przerwie.

5. Zdający na poziomie podstawowym otrzymuje do rozwiązania jeden arkusz egzaminacyjny, a na poziomie rozszerzonym dodatkowo drugi arkusz egzaminacyjny.

6. Opis egzaminu:

1. część pierwsza egzaminu dla obu poziomów polega na rozwiązaniu zestawu krótkich zadań badających rozumienie pojęć i umiejętności ich stosowania w prostych sytuacjach oraz zadań o charakterze problemowym, badających umiejętność zastosowania wiedzy,

1. część druga egzaminu dotyczy poziomu rozszerzonego i polega na rozwiązaniu zadań wymagających praktycznego rozumienia elementów metodologii matematyki (definicja, twierdzenie, założenie, dowód, korzystanie z twierdzenia, hipoteza, posługiwanie się definicją itp.).

7. Egzamin na poziomie rozszerzonym różni się od egzaminu na poziomie podstawowym zwiększeniem stopnia trudności i zakresu materiału programowego.

8. W obu częściach egzaminu zdający może korzystać z tablic matematycznych i kalkulatora (z wyjątkiem graficznego).

9. Ocenianie:

1. za rozwiązanie zadań z pierwszego arkusza zdający może otrzymać maksymalnie 40% całkowitej liczby punktów,

2. za rozwiązanie zadań z drugiego arkusza zdający może otrzymać maksymalnie 60% całkowitej liczby punktów.

10. Egzamin oceniany jest według kryteriów jednakowych w całym kraju.

V. WYMAGANIA EGZAMINACYJNE

W poniższej tabeli zastosowano skróty: C - cele edukacyjne, Z - zadania szkoły, T - treści, O - osiągnięcia. Numer przy każdym symbolu odnosi się do odpowiedniej części Podstawy Programowej.

Standardy zapisane wytłuszczoną czcionką dotyczą poziomu rozszerzonego egzaminu.

Standard		Opis wymagań Zdający potrafi:		Odniesienie do Podstawy programowej
Wykazać się znajomością i rozumieniem:
wskazanych pojęć, np. rozwiązania równania, funkcje oraz tych ich własności, które są konieczne do rozumienia wykonywanych obliczeń, własności funkcji, elementów geometrii i rachunku prawdopodobieństwa,		wykazać się znajomością i rozumieniem definicji z zakresu treści dla poziomu podstawowego i na tej podstawie rozpoznawać obiekty matematyczne, wykazać się znajomością i rozumieniem twierdzeń z zakresu treści dla poziomu podstawowego i zastosować wskazane twierdzenia,		C 1 Z 1 T 1 - 4 O 1
wskazanych algorytmów, np. rozwiązalności równania kwadratowego, wyznaczania n-tego wyrazu ciągu geometrycznego oraz typowych sytuacji, w których można się nimi posłużyć,		zastosować wskazany algorytm w typowej sytuacji,
wskazanych pojęć, np. logarytmu, pochodnej funkcji, twierdzeń dotyczących np. monotoniczności funkcji logarytmicznej, sinusów, związku pochodnej z monotonicznością funkcji oraz ich interpretacji w konkretnych sytuacjach.		wykazać się znajomością i rozumieniem definicji z zakresu treści dla poziomu rozszerzonego i na tej podstawie rozpoznawać obiekty matematyczne, wykazać się znajomością i rozumieniem twierdzeń z zakresu treści dla poziomu rozszerzonego i zastosować wskazane twierdzenia,
Stosować posiadaną wiedzę do rozwiązywania zadań teoretycznych i praktycznych, czyli:
posłużyć się znaną definicją, np. figur jednokładnych, twierdzeniem, np. o stosunku pól figur jednokładnych w typowej sytuacji,		rozpoznawać obiekty matematyczne, dostrzegać i zapisywać ich własności na podstawie definicji i twierdzeń,		C 1, 2 Z 1 T 1 - 4 O 1
rozwiązywać zadania wymagające przeprowadzenia, analogicznego rozumowania wg podanego schematu,		przeanalizować podany schemat rozumowania, dostrzegając jego istotne cechy, zanalizować nową sytuację, a następnie zastosować podany schemat rozumowania,		C 2, 3 Z 3 T 1 - 4 O 1
odczytywać informacje ilościowe, np. dotyczące argumentów i wartości funkcji oraz proste informacje jakościowe, np. dotyczące własności funkcji z tabel, diagramów i wykresów,		rozpoznać sposób zapisania danych, wybrać odpowiednie dane, porównywać odczytane informacje,		C 4 Z 2 T 1 - 4 O 3
posługiwać się miarą, np. długości, pola i objętości oraz przybliżeniami dziesiętnymi tych miar w prostych sytuacjach z życia codziennego,		zaplanować potrzebne obliczenia, uwzględniając właściwe jednostki miary (np.: długości, pola lub objętości), przeliczać (zamieniać) jednostki pola, długości lub objętości na inne jednostki tej samej miary, przybliżać wartości wyników obliczeń z zaplanowaną, stosowną do sytuacji dokładnością,		C 4 Z 2 T 1, 4 O 3
formułować proste zależności, np. rekurencyjnie; wyciągać wnioski z podanych zależności, np. typu funkcyjnego, wyrażonych równaniem; uzasadniać prawdziwość wniosków.		dostrzegać zależności na podstawie analizy danych i ich własności, określić i uzasadnić zależności między analizowanymi danymi,

Stosować metody matematyczne w sytuacjach problemowych, czyli:
podać opis matematyczny w postaci wyrażenia algebraicznego, funkcji, równania, nierówności, przekształcenia geometrycznego do podanej sytuacji (także praktycznej), i wykorzystać go do rozwiązania problemu,	dokonać analizy podanej sytuacji, wybrać odpowiedni do sytuacji opis matematyczny, opisać podaną sytuację,	C 2, 4 Z 3, 4, 5 T 1 - 4, O 4
dobrać odpowiedni algorytm do wskazanej sytuacji problemowej i ocenić przydatność uzyskanych wyników w typowej sytuacji,	dokonać analizy wskazanej sytuacji, wybrać algorytm przydatny do rozwiązania danego problemu, zastosować wybrany algorytm, zinterpretować otrzymane wyniki,	C 1, 4 Z 1, 3 T 1 - 4 O 1
przetworzyć informacje wyrażone w postaci wyrażenia algebraicznego, równania, wzoru lub wykresu funkcji, opisu wektorowego na inną formę ułatwiającą rozwiązanie problemu,	posługiwać się różnymi rodzajami opisu matematycznego, przekształcać jedną formę opisu na inną,	C 1 Z 1 T 1 - 4, O 1, 3
interpretować jakościowo informacje z tabel, diagramów, wykresów oraz ustalać i formułować między nimi proste zależności; wykorzystywać je w toku badania typowej sytuacji problemowej,	odczytywać odpowiednie dane z tabel, diagramów, wykresów, porównywać i określać zależności między odczytanymi danymi, wykorzystywać otrzymane wyniki do rozwiązania problemu,
stosować definicje i twierdzenia w rozwiązywaniu problemów.	rozróżnić definicje pojęć od twierdzeń dotyczących tych pojęć, dokonać wyboru definicji, twierdzeń potrzebnych do rozwiązania problemu, zastosować wybrane definicje, twierdzenia do poprawnego rozwiązania danego problemu,

Rozwiązywać zadania wymagające argumentowania i prowadzenia rozumowań typu matematycznego, czyli:
interpretować treść zadania, zapisywać warunki i zależności między obiektami, dobierać i zastosować odpowiednie definicje, twierdzenia, własności i algorytmy; analizować otrzymane wyniki,	zapisywać warunki i zależności wynikające z treści lub otrzymane podczas rozwiązywania zadania, dobierać definicje i twierdzenia odpowiednio do przyjętego sposobu rozwiązania, dokonać oceny zgodności otrzymanych wyników z warunkami zadania,	C 2 Z 3, 4, 5 T 1 - 4 O 1, 4
argumentować i uzasadniać wnioski oraz opisywać je w sposób czytelny i poprawny językowo,	opisywać i uzasadniać ustalone w trakcie rozwiązania wnioski, stosować poprawny język matematyczny,	C 1, 3, 4 Z 4, 5, 6 T 1 - 4 O 2, 4
przeprowadzić i zredagować pełny dowód twierdzenia.	wyróżnić założenia i tezę danego twierdzenia, sformułować dodatkowe wnioski wynikające z założeń twierdzenia i uzasadniać je w oparciu o inne znane twierdzenia i definicje, skorzystać z założeń i dodatkowych wniosków w dowodzie tezy, podać pełne uzasadnienie całości rozumowania posługując się poprawnym językiem matematycznym.

Opis wymagań egzaminacyjnych w zakresie
treści programowych

Poziom podstawowy

Dział	ZAKRES TREŚCI	ZDAJĄCY POTRAFI:
1. LICZBY RZECZYWISTE	Usystematyzowanie wiadomości o liczbach wymiernych	planować i wykonywać obliczenia, porównywać liczby wymierne, przedstawiać liczby wymierne w różnych postaciach (ułamek zwykły, liczba dziesiętna),
		Przykłady liczb niewymiernych; przybliżenia dziesiętne liczb rzeczywistych	usuwać niewymierność z mianownika lub licznika ułamka, wyznaczać przybliżenia dziesiętne danej liczby rzeczywistej z zadaną dokładnością (również z użyciem kalkulatora), szacować wyniki obliczeń z zadaną dokładnością, wykonywać działania na wyrażeniach algebraicznych (w tym stosować wzory skróconego mnożenia), wyznaczać sumę, iloczyn i różnicę przedziałów liczbowych oraz innych podzbiorów zbioru liczb rzeczywistych,
		Obliczenia procentowe	posługiwać się procentem w rozwiązywaniu zadań, oceniać zmianę wielkości jaka nastąpiła, porównywać wielkości,
		Potęgowanie liczb rzeczywistych	wykonywać działania na potęgach o wykładnikach całkowitych i wymiernych,
	2. FUNKCJE	Pojęcie funkcji	określać funkcję (wzorem, tabelką, wykresem, grafem, opisem słownym),
		Przykłady wykresów funkcji liczbowych; przekształcanie wykresów funkcji	wskazać wykres funkcji liczbowej, sporządzić wykresy funkcji: y = -f(x), y = f(-x), y = -f(-x), y = f(x-a)+b na podstawie danego wykresu funkcji y = f(x),
		Odczytywanie własności funkcji liczbowej z wykresu	określać z wykresu: dziedzinę funkcji, zbiór wartości funkcji, miejsca zerowe funkcji, monotoniczność funkcji, znaki funkcji,
		Funkcja liniowa	sporządzać wykres funkcji liniowej, interpretować współczynniki w równaniu kierunkowym prostej,
2. FUNKCJE - c. d.	Funkcja kwadratowa	wyznaczać miejsca zerowe funkcji kwadratowej, przedstawiać funkcję kwadratową w różnych postaciach (ogólnej, iloczynowej, kanonicznej), sporządzać wykresy funkcji kwadratowych, odczytać własności funkcji kwadratowej z jej wykresu, wyznaczać największą i najmniejszą wartość funkcji kwadratowej w przedziale, wykorzystać własności funkcji kwadratowej i jej wykresu do rozwiązywania zadań optymalizacyjnych,
3. RÓWNANIA I NIERÓWNOŚCI	Równania i nierówności liniowe z jedną niewiadomą	rozwiązywać równania i nierówności liniowe z jedną niewiadomą, rozwiązywać zadania tekstowe prowadzące do równań i nierówności liniowych z jedną niewiadomą, układać zadania tekstowe do podanych równań i nierówności liniowych z jedną niewiadomą,
		Równania i nierówności liniowe z dwiema niewiadomymi; układy równań liniowych i ich interpretacja geometryczna	graficznie przedstawiać równania i nierówności liniowe z dwiema niewiadomymi, rozwiązywać algebraicznie i graficznie układy równań liniowych z dwiema niewiadomymi, rozwiązywać zadania tekstowe prowadzące do układów równań liniowych z dwiema niewiadomymi, układać zadania tekstowe do podanych układów równań liniowych z dwiema niewiadomymi,
		Równania i nierówności kwadratowe z jedną niewiadomą i ich interpretacja geometryczna	rozwiązywać równania i nierówności kwadratowe z jedną niewiadomą, graficznie rozwiązywać równania i nierówności kwadratowe z jedną niewiadomą, rozwiązywać zadania tekstowe prowadzące do równań i nierówności kwadratowych z jedną niewiadomą, obliczać wartości wyrażeń zawierających sumy i iloczyny pierwiastków równania kwadratowego (wzory Viète'a),
		Przykłady prostych równań i nierówności stopnia trzeciego	rozwiązywać równania i nierówności stopnia trzeciego z jedną niewiadomą poprzez rozkład na czynniki stosując: wyłączanie wspólnego czynnika, grupowanie wyrazów i wzory skróconego mnożenia,
		Proporcjonalność prosta i odwrotna; wykres proporcjonalności prostej i odwrotnej	sporządzać wykresy proporcjonalności prostej i odwrotnej, opisać i zastosować proporcjonalność prostą i odwrotną w rozwiązywaniu zadań,
3. - c d.	Proste równania i nierówności wymierne	rozwiązywać równania typu: i nierówności typu: ,
4. CIĄGI LICZBOWE	Przykłady ciągów liczbowych (w tym ciągów rekurencyjnych)	określać ciąg wzorem ogólnym lub rekurencyjnym, wyznaczać wyrazy ciągu określonego wzorem ogólnym lub rekurencyjnym, szkicować wykres danego ciągu, podać własności ciągu na podstawie jego wykresu,
		Własności ciągu	badać monotoniczność ciągu z wykorzystaniem definicji,
		Ciąg arytmetyczny i ciąg geometryczny: suma wyrazów ciągu arytmetycznego, suma wyrazów ciągu geometrycznego	badać czy ciąg jest arytmetyczny lub geometryczny na podstawie definicji, wyznaczać ciąg arytmetyczny lub geometryczny na podstawie wskazanych danych, obliczać sumę n kolejnych wyrazów ciągu arytmetycznego i geometrycznego, stosować własności ciągu arytmetycznego i geometrycznego w zadaniach (także tekstowych),
		Procent składany	stosować procent składany w zadaniach i podjąć decyzję na podstawie obliczeń,
		Szereg geometryczny	badać warunek istnienia sumy szeregu geometrycznego, obliczać sumę szeregu geometrycznego, zamieniać ułamek okresowy na zwykły, stosować wzór na sumę szeregu geometrycznego w zadaniach,
	5. ELEMENTY RACHUNKU PRAWDOPODOBIEŃSTWA	Elementy kombinatoryki	obliczać wartości n! oraz , stosować wzory: na liczbę permutacji, kombinacji oraz wariacji z powtórzeniami i bez powtórzeń, rozwiązywać zadania tekstowe z zastosowaniem wzorów kombinatorycznych,
		Prawdopodobieństwo i jego związek z częstością; przykłady obliczania prawdopodobieństwa	określać zbiór (skończony) zdarzeń elementarnych doświadczenia losowego, wyznaczać liczbę wszystkich zdarzeń elementarnych oraz liczbę zdarzeń elementarnych sprzyjających danemu zdarzeniu losowemu, wyznaczać częstość zdarzeń w doświadczeniu losowym, obliczać prawdopodobieństwa zdarzeń losowych na podstawie definicji klasycznej oraz za pomocą drzewa,
5. - c d.	Przykłady praktycznego zastosowania statystyki	odczytywać dane statystyczne z tabel, diagramów i wykresów, przedstawiać dane empiryczne w postaci tabel, diagramów i wykresów, przeprowadzić analizę ilościową przedstawianych danych,
6. GEOMETRIA	Figury płaskie i ich własności	zbadać wzajemne położenie prostych w ujęciu syntetycznym i analitycznym, wyznaczać odległość: dwóch punktów, punktu od prostej, dwóch prostych równoległych - w ujęciu syntetycznym i analitycznym, określać wzajemne położenie prostej i okręgu oraz dwóch okręgów, wykonywać działania na wektorach (dodawanie, mnożenie przez liczbę, iloczyn skalarny) - w ujęciu analitycznym i syntetycznym, posługiwać się własnościami: symetralnej odcinka, dwusiecznej kąta, środkowych boków trójkąta, kątów w kole, korzystać z własności wielokątów wypukłych opisanych na okręgu i wpisanych w okrąg, określać własności podstawowych figur płaskich (odcinek, półprosta, prosta, kąt, wielokąt, okrąg , koło) i posługiwać się nimi,
		Przekształcenia geometryczne na płaszczyźnie	stosować własności: izometrii (symetrii i przesunięcia), jednokładności i podobieństwa w rozwiązywaniu zadań, stosować cechy przystawania i podobieństwa figur w rozwiązywaniu zadań,
		Konstrukcje geometryczne	konstruować (rysować przy pomocy cyrkla i linijki): proste prostopadłe i proste równoległe, symetralną odcinka, dwusieczną kąta, odcinek o wskazanej długości z zastosowaniem twierdzenia Talesa lub twierdzenia Pitagorasa, kąt przystający do danego kąta, wielokąt przystający do danego wielokąta, styczną do okręgu, okrąg styczny zewnętrznie lub wewnętrznie do danego okręgu, styczną do dwóch okręgów, okrąg wpisany w wielokąt wypukły i opisany na wielokącie wypukłym, obraz figury w przekształceniu geometrycznym,
	6. GEOMETRIA - c. d.	Elementy trygonometrii	stosować miarę łukową i stopniową kąta wypukłego, obliczać wartości funkcji trygonometrycznych kąta wypukłego oraz wyznaczać miarę kąta, gdy dana jest wartość funkcji trygonometrycznej tego kąta, stosować związki między funkcjami trygonometrycznymi tego samego kąta: do obliczania wartości funkcji trygonometrycznych kąta wypukłego oraz do dowodzenia tożsamości trygonometrycznych, stosować wzory redukcyjne dla kątów wypukłych,
		Własności miarowe figur na płaszczyźnie	stosować twierdzenie Talesa (proste i odwrotne), stosować: twierdzenie kosinusów (twierdzenie Pitagorasa proste i odwrotne), twierdzenie sinusów, związki miarowe w trójkącie prostokątnym oraz funkcje trygonometryczne, obliczać obwody i pola podstawowych figur płaskich (także z zastosowaniem funkcji trygonometrycznych),
		Figury geometryczne w przestrzeni	badać wzajemne położenia prostych i płaszczyzn w przestrzeni, stosować pojęcia: kąta dwuściennego, kąta między prostą i płaszczyzną w rozwiązywaniu zadań, badać własności podstawowych figur przestrzennych: graniastosłupów (prostych, prawidłowych) i ostrosłupów (w tym prawidłowych), badać własności brył obrotowych (kuli, walca, stożka), wyznaczać pola powierzchni i objętości wielościanów i brył obrotowych, wyznaczać przekroje płaskie wielościanów i brył obrotowych.

Uzupełnienie do poziomu rozszerzonego

Dział	ZAKRES TREŚCI	ZDAJĄCY POTRAFI:
1. LICZBY RZECZYWISTE	Zbiory	wyznaczać sumę, iloczyn, różnicę i dopełnienie zbiorów, stosować własności działań na zbiorach,
		Wartość bezwzględna	stosować definicję i własności wartości bezwzględnej liczby rzeczywistej (np.: , , ),
	2. FUNKCJE	Własności funkcji	określać dziedzinę, zbiór wartości, miejsca zerowe i znaki funkcji, badać równość funkcji, badać różnowartościowość, monotoniczność, parzystość, nieparzystość, okresowość funkcji z wykorzystaniem definicji, wyznaczać wzór i szkicować wykres funkcji odwrotnej do danej, składać funkcje, sporządzić wykresy funkcji: na podstawie danego wykresu funkcji ,
		Wielomiany i funkcje wymierne	wykonywać działania na wielomianach jednej zmiennej, rozkładać wielomiany na czynniki z wykorzystaniem twierdzenia Bézout oraz twierdzenia o wymiernych pierwiastkach wielomianu o współczynnikach całkowitych, wykonywać działania w zbiorze funkcji wymiernych, szkicować wykresy funkcji homograficznych,
		Funkcje potęgowe, wykładnicze i logarytmiczne	posługiwać się własnościami funkcji, szkicować wykresy, stosować twierdzenia dotyczące logarytmowania wyrażeń algebraicznych,
		Funkcje trygonometryczne	stosować definicje funkcji trygonometrycznych zmiennej rzeczywistej, stosować wzory: redukcyjne, funkcji trygonometrycznych sumy i różnicy kątów, sum i różnic funkcji trygonometrycznych oraz funkcji trygonometrycznych wielokrotności kąta, szkicować wykresy funkcji trygonometrycznych z uwzględnieniem zmiany ich okresowości (np. ),
2. FUNKCJE - c. d.	Elementy analizy matematycznej	obliczać granice funkcji w punkcie i w nieskończoności, wyznaczać asymptoty wykresu funkcji (poziomą, pionową, ukośną), badać ciągłość funkcji w przedziale, korzystać z ciągłości funkcji przy badaniu własności funkcji oraz rozwiązywaniu równań, obliczać na podstawie definicji pochodną funkcji w punkcie, korzystać z geometrycznej interpretacji pochodnej funkcji w punkcie (np. wyznaczać równanie stycznej do wykresu funkcji), obliczać pochodne funkcji elementarnych i funkcji złożonych, wyznaczać przedziały monotoniczności funkcji, wyznaczać ekstrema funkcji, wyznaczać najmniejszą i największą wartość funkcji w przedziale domkniętym, zbadać przebieg zmienności danej funkcji i sporządzić jej wykres, stosować pochodną do rozwiązywania zadań optymalizacyjnych,
3. RÓWNANIA I NIERÓWNOŚCI	Rozwiązywanie równań, nierówności i ich układów	rozwiązywać równania i nierówności wielomianowe i wymierne, rozwiązywać równania i nierówności trygonometryczne, rozwiązywać równania i nierówności wykładnicze i logarytmiczne, graficznie przedstawiać równania (nierówności) drugiego stopnia z dwiema niewiadomymi - okrąg (koło), suma dwóch prostych (kątów), graficznie przedstawiać układy nierówności liniowych z dwiema niewiadomymi, rozwiązywać układy równań liniowych z trzema niewiadomymi, rozwiązywać algebraicznie i graficznie układy równań z dwiema niewiadomymi, z których przynajmniej jedno jest stopnia drugiego, rozwiązywać równania, nierówności i układy wymienionych typów z wartością bezwzględną i z parametrem,
4. CIĄGI LICZBOWE	Zasada indukcji matematycznej	stosować zasadę indukcji matematycznej do dowodzenia twierdzeń,
		Granica ciągu	stosować twierdzenia o granicy sumy, różnicy, iloczynu i ilorazu ciągów zbieżnych,
	5. ELEMENTY RACHUNKU PRAWDOPODOBIEŃSTWA	Prawdopodobieństwa zdarzeń losowych	w skończonym zbiorze zdarzeń elementarnych: obliczać prawdopodobieństwo zdarzeń na podstawie własności prawdopodobieństwa, obliczać prawdopodobieństwo warunkowe i całkowite, badać niezależność zdarzeń, stosować schemat Bernoulliego do obliczania prawdopodobieństwa,
		Przykłady praktycznego zastosowania statystyki	przeprowadzać analizę ilościową i jakościową przedstawianych danych,
	6. GEOMETRIA	Figury geometryczne w przestrzeni	badać własności wielościanów, wyznaczać przekroje płaskie wielościanów i brył obrotowych, badać figury wpisane w inną figurę (np. ostrosłup wpisany w kulę),
		Przekształcenia geometryczne w przestrzeni	stosować własności izometrii (symetrii, obrotu i przesunięcia) i podobieństwa w ustalaniu własności figur.

VI. przykładowe arkusze egzaminacyjne i  schematy oceniania

WERSJA A

Wpisuje ZDAJĄcy po otrzymaniu ARKUSZA

KOD ZDAJĄCEGO

WPISAĆ PO ROZKODOWANIU PRACY

IMIĘ

ARKUSZ I

NAZWISKO

PP

EGZAMIN MATURALNY

Z MATEMATYKI

POZIOM PODSTAWOWY Arkusz egzaminacyjny I

MAJ - CZERWIEC ROK 2002

MATEMATYKA

Czas pracy 120 minut

Informacje

Proszę sprawdzić, czy arkusz egzaminacyjny zawiera ...... stron. Ewentualny brak należy zgłosić przewodniczącemu komisji. Proszę rozwiązać zadania. Przy każdym zadaniu podana jest możliwa do uzyskania liczba punktów. Za rozwiązanie wszystkich zadań można otrzymać łącznie 40 punktów. Odpowiedzi należy zapisać dokładnie i czytelnie, pokazując drogę ich uzyskania. Należy użyć tylko niebieskiego lub czarnego długopisu albo pióra. Proszę nie używać korektora. W przypadku podania błędnej odpowiedzi należy dany fragment pracy wyraźnie przekreślić, a przekreślenie podpisać. Podczas egzaminu można korzystać z tablic matematycznych, cyrkla i linijki oraz kalkulatora, z wyjątkiem graficznego. Życzymy powodzenia!

Uzyskane punkty

Nr zad.

Punkty

Suma

Egzaminator

WPISAĆ po otrzymaniu WYPEŁNIONEGO ARKUSZA

Kod

Imię

Nazwisko

Nakład .............itp.

Rozwiąż równanie:
.

Aby wyznaczyć ułamek zwykły, który ma rozwinięcie dziesiętne 0,(172) można postąpić następująco:

(1)

(2)

Po odjęciu stronami równania oznaczonego (1) od równania oznaczonego (2) mamy:

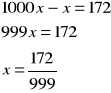
Przeprowadź analogiczne rozumowanie i znajdź ułamek zwykły, który ma rozwinięcie dziesiętne 0,(75).

Okrągły obrus został w całości wykrojony z materiału w kształcie kwadratu o boku 4 m. Wiedząc, że materiał został maksymalnie wykorzystany, oblicz ile metrów ozdobnego sznura potrzeba na obszycie brzegu tego obrusa. Podaj wynik z dokładnością do 0,1 m.

Dane są punkty: A(-3, -1), B(-1, 0), C(-2, 2).

Oblicz współrzędne i długość wektora
.

Pan Kowalski założył w swojej firmie zamek z czterocyfrowym kodem. Aby mógł łatwiej zapamiętać, wybrał kod, w którym suma dwóch pierwszych cyfr równa jest 12, a suma dwóch ostatnich cyfr 10. Ile miał możliwości wyboru kodu?

Drużyna siatkówki składa się z sześciu zawodników. Do kontroli antydopingowej wybiera się dwóch zawodników. Jakie jest prawdopodobieństwo, że kontroli poddany zostanie kapitan drużyny?

Wydatki rodziny Kowalskich w latach 1997 - 1998 przedstawiono na wykresie.

Przyjmujemy, że w roku 1997 całkowity dochód brutto tej rodziny wynosił 50000 zł, zaś w roku 1998 - 45000 zł.

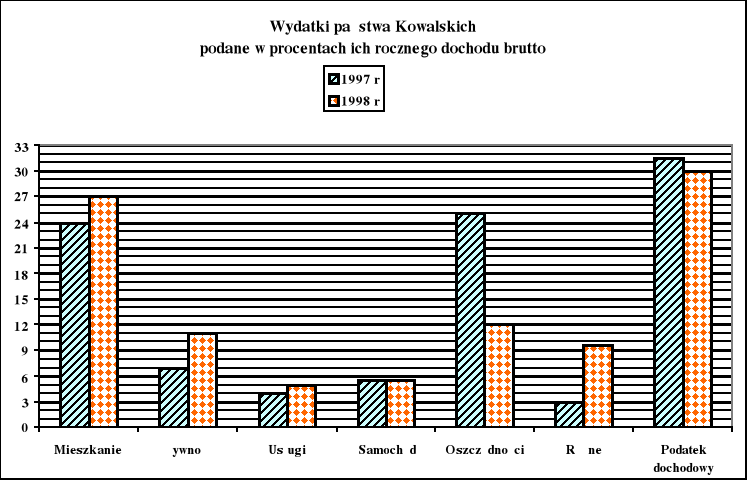
1. W 1997 r państwo Kowalscy wydali 49% swojego dochodu brutto na dwie spośród pozycji przedstawionych na wykresie. Ile złotych wyniosły ich wydatki na te same cele w 1998 r.?

2. Dochód brutto jest sumą dochodu pani Kowalskiej i pana Kowalskiego. W 1997 r. dochody obojga wynosiły po 25000 zł. Gdyby w 1998 roku dochód pana Kowalskiego był o 10% większy w porównaniu z jego dochodem w roku 1997, to o ile procent musiałby zmniejszyć się w roku 1998 dochód pani Kowalskiej w porównaniu z rokiem 1997?

Pan X umówił się z panem Y, że będzie mu wypłacał codziennie przez trzy tygodnie pieniądze, przy czym pierwszego dnia 10 zł, drugiego 20 zł, trzeciego 30 zł, czwartego 40 zł itd. W zamian pan Y wypłaci mu pierwszego dnia 1 grosz, drugiego 2 grosze, trzeciego 4 grosze, czwartego 8 groszy itd. Który z panów zyska na tej umowie i ile?

Pewna firma telekomunikacyjna proponuje abonentowi do wyboru dwa warianty opłat miesięcznych za telefon:

I - za każdy impuls 20 groszy i jednocześnie brak opłaty stałej;

II - za każdy impuls 8 groszy i jednocześnie opłatę stałą w wysokości 12 złotych.

1. Dla każdej z możliwości zapisz w postaci wzoru zależność między miesięczną opłatą za telefon a liczbą wykorzystanych w miesiącu impulsów.

2. Którą z możliwości należy wybrać, jeżeli zakładamy, że miesięcznie wykorzystuje się 120 impulsów?

3. Oblicz, przy jakiej liczbie impulsów wybór pomiędzy podanymi wariantami opłat nie wpływa na wysokość opłat.

2. MODEL ODPOWIEDZI I SCHEMAT OCENIANIA ARKUSZA EGZAMINACYJNEGO I - POZIOM PODSTAWOWY - WERSJA A

Nr zadania	Etapy rozwiązania zadania	Liczba punktów
1.	Pogrupowanie wyrazów	1
		Rozłożenie na czynniki:	1
		Sformułowanie poprawnej odpowiedzi:	1
	2.	Obliczenie zysku telewizji Polsat: 700 mln zł	1
		Obliczenie zysku telewizji TVP 2: 220 mln zł	1
		Obliczenie różnicy zysków i sformułowanie odpowiedzi: 480 mln zł	1
	3.	Zapisanie równości (1):	1
		Zapisanie równości (2):	1
		Obliczenie ułamka:	1
	4.	Obliczenie długości promienia koła: r = 2 m	1
		Obliczenie obwodu koła:	1
		Sformułowanie poprawnej odpowiedzi: 12,6 m.	1
	5.	Wyznaczenie współrzędnych wektora	1
		Wyznaczenie współrzędnych wektora	1
		Obliczenie długości wektora	1
	6.	Wyznaczenie liczby możliwych wyborów dwóch pierwszych cyfr - 7	1
		Wyznaczenie liczby możliwych wyborów dwóch ostatnich cyfr - 9	1
		Wyznaczenie liczby wszystkich możliwych kodów - 63	1
	7.	Obliczenie liczby wszystkich zdarzeń elementarnych - 15	1
		Obliczenie liczby zdarzeń sprzyjających - 5	1
		Obliczenie prawdopodobieństwa:	1
	8.	Wskazanie dwóch pozycji (mieszkanie i oszczędności), na które państwo Kowalscy wydali w 1997 r. 49% swojego dochodu brutto	1
		Obliczenie kwoty wydanej na te same cele w 1998 r. - 17550 zł	1
		Podanie rocznego dochodu pana Kowalskiego w 1998 r. - 27500 zł	1
		Obliczenie, o ile procent zmniejszył się dochód pani Kowalskiej w 1998 r. - o 30%	1
	9.	Opisanie ciągu arytmetycznego:	1
		Opisanie ciągu geometrycznego:	1
		Obliczenie sumy ciągu arytmetycznego	1
		Obliczenie sumy ciągu geometrycznego	1
		Sformułowanie pełnej odpowiedzi	1

10.	a) Jeśli n - liczba impulsów, y - opłata miesięczna:
		za zapisanie zależności dla wariantu I: za zapisanie zależności dla wariantu II:	1 1
		b) za obliczenie opłaty w wariancie I: (n = 120); 24 zł za obliczenie opłaty w wariancie II: 21,6 zł	1
		c) za zapisanie równania: za rozwiązanie równania i sformułowanie poprawnej odpowiedzi: n =100	1 1
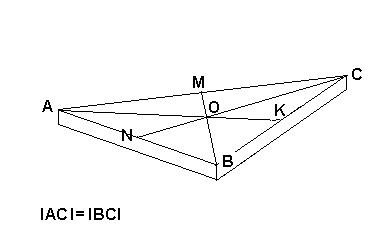
	11.	Wskazanie 3 par trójkątów o równych polach: BKO i COK, AOM i CMO oraz ANO i BON	2
		Wskazanie pary trójkątów o równych polach: BKO i AOM	2
		Wskazanie np. pary trójkątów ABK i AKC o równych polach i sformułowanie wniosku o równości pól trójkątów: ANO i AOM	1

Za prawidłowe rozwiązanie każdego z zadań inną metodą (zgodną z poleceniem) od przedstawionej w schemacie przyznajemy maksymalną liczbę punktów.

Wpisuje ZDAJĄcy po otrzymaniu ARKUSZA

KOD ZDAJĄCEGO

WPISAĆ PO ROZKODOWANIU PRACY

IMIĘ

ARKUSZ II

NAZWISKO

PR

EGZAMIN MATURALNY

Z MATEMATYKI

POZIOM ROZSZERZONY Arkusz egzaminacyjny II

MAJ - CZERWIEC ROK 2002

MATEMATYKA

Czas pracy 150 minut

Informacje

Proszę sprawdzić, czy arkusz egzaminacyjny zawiera ..... stron. Ewentualny brak należy zgłosić przewodniczącemu komisji. Proszę rozwiązać zadania. Przy każdym zadaniu podana jest możliwa do uzyskania liczba punktów. Za rozwiązanie wszystkich zadań można otrzymać łącznie 60 punktów. Odpowiedzi należy zapisać dokładnie i czytelnie, pokazując drogę ich uzyskania. Należy użyć tylko niebieskiego lub czarnego długopisu albo pióra. Proszę nie używać korektora. W przypadku podania błędnej odpowiedzi należy dany fragment pracy wyraźnie przekreślić, a przekreślenie podpisać. Podczas egzaminu można korzystać z tablic matematycznych, cyrkla i linijki oraz kalkulatora, z wyjątkiem graficznego. Życzymy powodzenia!

Uzyskane punkty

Nr zad.

Punkty

Suma

Egzaminator

WPISAĆ po otrzymaniu WYPEŁNIONEGO ARKUSZA

Kod

Imię

Nazwisko

Nakład .............itp.

Zbadaj ciągłość funkcji:

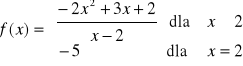
Odpowiedź uzasadnij.

Zaznacz w układzie współrzędnych zbiór punktów, których współrzędne spełniają nierówność:
.

Dla jakich x prawdziwa jest nierówność: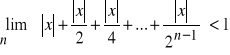
?

W pewnej grupie młodzieży dane dotyczące płci oraz koloru oczu ilustrują wykresy: I, II i III.

Wykorzystując tożsamość:
wykaż, że
jest rozwiązaniem równania:
.

Naszkicuj wykres funkcji:

.

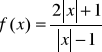
Na podstawie wykresu funkcji odczytaj przedziały, w których funkcja ta przyjmuje wartości ujemne.

Przekątna przekroju osiowego walca ma długość równą
. Jaką największą objętość może mieć ten walec ?

Rozwiąż nierówność
przy założeniu, że wartość parametru m należy do przedziału (0; 1).

W równoległoboku ABCD dane są:
, zaś środkiem boku AB jest punkt
.

Wyznacz równanie prostej przechodzącej przez wierzchołki C, D.

Wyznacz równanie prostej CE zawierającej wysokość poprowadzoną z wierzchołka C i przecinającej prostą AB w punkcie E.

Opisz przy pomocy układu nierówności liniowych zbiór wszystkich punktów należących do trójkąta BCE.

6. MODEL ODPOWIEDZI I SCHEMAT OCENIANIA ARKUSZA EGZAMINACYJNEGO II - POZIOM ROZSZERZONY

Nr zadania	Etapy rozwiązania zadania	Maksymalna liczba punktów
13.	Obliczenie granicy funkcji w punkcie :	2
		Porównanie wartości granicy i wartości funkcji oraz stwierdzenie ciągłości w punkcie x = 2	2
		Stwierdzenie ciągłości w zbiorze R (z komentarzem)	1
	14.	Utworzenie układu nierówności:	2
		Ilustracja graficzna zbioru:	2
	15.	Obliczenie sumy n początkowych wyrazów ciągu geometrycznego	2
		Obliczenie granicy:	1
		Rozwiązanie nierówności z wartością bezwzględną:	1
	16.	Poprawne odczytanie danych z wykresów (opis zdarzeń losowych)	2
		Obliczenie prawdopodobieństwa zdarzenia: 0,24	2
	17.	Sprowadzenie tożsamości do postaci :	2
		Podstawienie: do równania i uzyskanie tezy	2
	18.	Zapisanie wzoru funkcji bez wartości bezwzględnej:	2
		Narysowanie wykresu funkcji f w przypadku (*)	1
		Narysowanie wykresu funkcji f w przypadku (**)	1
		Odczytanie przedziału, w którym funkcja przyjmuje wartości ujemne: (-1;1)	1
	19.	Wyznaczenie zależności między długością promienia podstawy i długością wysokości walca: - 1 punkt ; - 1 punkt	2
		Wyznaczenie funkcji objętości walca: .	2
		Określenie dziedziny funkcji objętości: .	1
		Obliczenie pochodnej funkcji objętości: .	1
		Wyznaczenie miejsca zerowego pochodnej: .	2
		Zbadanie znaku pochodnej.	1
		Uzasadnienie, że w punkcie 2 wartość funkcji jest największa.	2
		Wyznaczenie wartości największej: .	1

20.	Ustalenie dziedziny nierówności:	2
		Wykonanie podstawienia pomocniczego np.	1
		Rozwiązanie nierówności :	2
		Rozwiązanie nierówności wykładniczych:	1 2
		Wyznaczenie zbioru rozwiązań nierówności:	2
		Sformułowanie poprawnej odpowiedzi	1
	21.	Sporządzenie rysunku wraz z oznaczeniami	1
		Wyznaczenie współrzędnych punktów: A, B, C, (po 1 pkt.)	3
		Określenie równań prostych AB, CD, CE, BC (po 1 pkt.)	4
		Opisanie przy pomocy układu nierówności liniowych:	3

Za prawidłowe rozwiązanie każdego z zadań inną metodą (zgodną z poleceniem) od przedstawionej w schemacie przyznajemy maksymalną liczbę punktów.

VII. INFORMACJE

Zreformowane egzaminy maturalne po raz pierwszy będą zdawane przez absolwentów szkół ponadpodstawowych, którzy urodzili się w 1983 roku, czyli dla absolwentów szkół czteroletnich będzie to w maju 2002 roku, dla absolwentów szkół pięcioletnich w maju 2003. Oprócz sesji majowych przewidziane jest wprowadzenie od stycznia 2003 roku sesji styczniowej, równoważnej z sesją majową. Każdy, kto nie przystąpił do egzaminu w maju, albo nie zdał egzaminu z jednego lub wszystkich przedmiotów, lub postanowił poprawić ocenę z jednego lub kilku przedmiotów - będzie mógł przystąpić do egzaminu ponownie już w styczniu.

Sesja egzaminacyjna będzie trwała około półtora miesiąca, każdego dnia będzie zdawany inny przedmiot, a nie jak obecnie wszystkie dodatkowe przedmioty jednego dnia. Podobnie języki obce będą zdawane w różnych dniach, a nie jednego dnia wszystkie.

Pierwsze egzaminy pisemne rozpoczną się więc około 5-6 maja i zakończą około 10 czerwca. Wyniki będą ogłoszone na przełomie czerwca i lipca.

Egzaminy ustne, które mają poprzedzać egzaminy pisemne będą organizowane już w kwietniu. Będą one musiały być zakończone do 20 kwietnia, więc zależnie od liczby zdających w danej szkole początek ich należy zaplanować na pierwszy lub drugi tydzień miesiąca.

Generalnie, każdy zdający będzie pisał egzamin maturalny w szkole, którą ukończył. Odstępstwa od tej zasady będą w czterech przypadkach:

• jeżeli szkoła nie będzie spełniała wymogów stawianych centrom egzaminacyjnym (odpowiednio duża sala, odpowiednio oświetlona, wyizolowana od nadmiernego hałasu itp.),

• jeżeli zdawany przedmiot będzie przedmiotem rzadkim - wybranym przez małą liczbę osób i w związku z tym organizowana będzie jedna komisja egzaminacyjna dla kilku szkół (np. greka lub filozofia),

• jeżeli szkoła nie będzie w stanie zapewnić odpowiednich warunków zdawania egzaminu ze względu na niepełnosprawność zdającego (np. brak komputera z drukarką z alfabetem brajlowskim dla osoby niewidomej),

• jeżeli wolą zdającego będzie zdawanie matury w innym miejscu niż ukończona szkoła.

Egzaminy będą organizowane i sprawdzane przez okręgowe komisje egzaminacyjne właściwe dla obszaru zamieszkania zdającego. W przypadku uczęszczania do szkoły w innym województwie (poza miejscem zamieszkania) zdający będzie mógł przystąpić do egzaminu w szkole, którą kończył.

Mapa na wewnętrznej stronie okładki obrazuje zasięg terytorialny poszczególnych komisji, natomiast adresy zamieszczone są na okładce zeszytu.

ANEKS

PRZYKŁADY ROZWIĄZAŃ ARKUSZY EGZAMINACYJNYCH

1744

3

10

53

Arkusz egzaminacyjny I

Wersja B

Poziom

podstawowy

120 minut

Arkusz egzaminacyjny I

Wersja A

Poziom

podstawowy

120 minut

ZADANIE 1

3 pkt.

ZADANIE 2

3 pkt.

Obok, na wykresie kołowym, przedstawiono procentowy udział stacji telewizyjnych w zyskach z reklam w 1999 roku. Wiedząc, że w 1999 roku cały zysk z reklam wyniósł 2 miliardy złotych, oblicz o ile więcej pieniędzy uzyskała telewizja Polsat niż TVP 2.

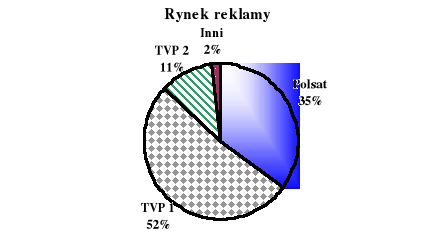
ZADANIE 3

3 pkt.

ZADANIE 4

3 pkt.

ZADANIE 5

3 pkt.

ZADANIE 6

3 pkt.

ZADANIE 7

3 pkt.

ZADANIE 8

4 pkt.

ZADANIE 13

5 pkt.

ZADANIE 9

5 pkt.

ZADANIE 10

5 pkt.

ZADANIE 11

5 pkt.

Grupa sześciu przyjaciół kupiła tort w kształcie graniastosłupa prostego, którego jedną z podstaw jest trójkąt równoramienny ABC (patrz rysunek). W trakcie dyskusji
- jak podzielić tort na 6 „równych” części, Krysia przypomniała sobie własności środkowych dowolnego trójkąta i przecięła tort prostopadle do podstawy wzdłuż linii AK, BM i NC, gdzie punkty K, M, N są środkami odpowiednich boków trójkąta ABC. Czy Krysia miała rację? Odpowiedź uzasadnij.

ZADANIE 14

4 pkt.

ZADANIE 15

4 pkt.

ZADANIE 16

4 pkt.

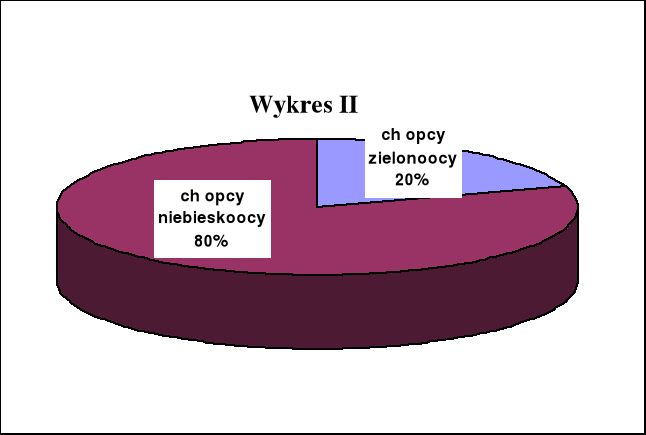
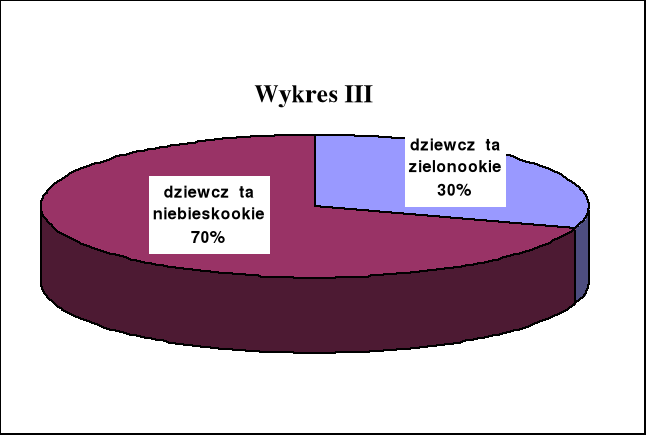
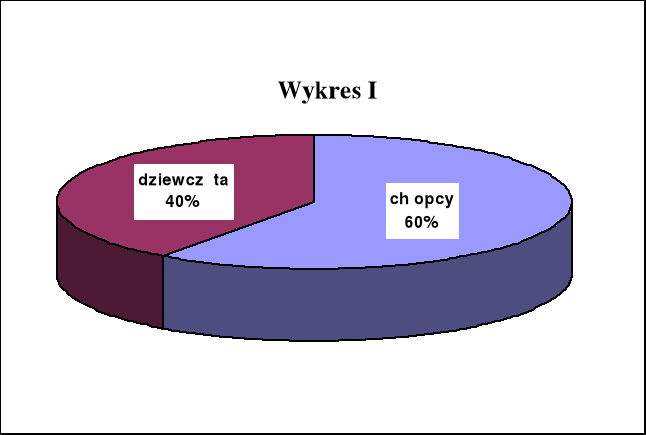
Wybrano losowo jedną osobę z tej grupy. Jakie jest prawdopodobieństwo, że ma ona zielone oczy?

ZADANIE 17

4 pkt.

ZADANIE 18

5 pkt.

ZADANIE 19

12 pkt.

ZADANIE 20

11 pkt.

ZADANIE 21

11 pkt.

Arkusz egzaminacyjny II

Poziom

rozszerzony

150 minut

Arkusz egzaminacyjny I

Wersja B

Poziom

podstawowy

120 minut

Arkusz egzaminacyjny I

Wersja A

Poziom

podstawowy

120 minut

Arkusz egzaminacyjny II

Poziom

rozszerzony

150 minut

---