OBLICZENIA DLA POMIARU 1

1. Strumień ciepła oblicza się na podstawie wzoru:

V_k - objętość kondensatu [m³]

ρ - gęstość kondensatu [kg/m³]

- czas napełniania się latarki [s]

r - ciepło kondensacji [J/kg].

Kondensat w temperaturze 40,0 [ºC]

Parametry kondensatu w latarce pomiarowej:

-Gęstość kondensatu ρ=992 [kg/m³]

-Ciepło kondensacji r=2406 [kJ/kg]

Do obliczeń przyjmuje temperaturę wrzenia i temperaturę kondensatu równą T=100[^oC],

2. Dla powietrza w temperaturze średniej:

t_2wlot- temperatura powietrza wlotowego do aparatury [^oC]

t_2wylot- temperatura powietrza wylotowego z aparatury [^oC]

Dla tej temperatury określam pozostałe parametry.

Gęstość	lepkość	Ciepło właściwe	Przew. Cieplne
ρp	[Pas]	Cw [J/kgK]	Λ [W/mK]
1,0853	1,73·10^-5	1014	0,0273

Obliczenie temperatury ∆T₁ ∆T₁=T_kond.-T_p.wlotowego =100-23=77 [ K]

Obliczenie temperatury ∆T₂ ∆T₂=T_pary-T_p.wylotowego =100-61,6=38,4 [K]

Obliczenie średniej logarytmicznej ∆T_e

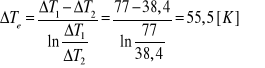
Obliczenie współczynnika wnikania ciepła α₁

Obliczenie liczby Reynoldsa

Obliczenie liczby Nusselta

Obliczenia teoretyczne:

Obliczenie liczby Prandtla

2

Obliczenie liczby Nusselta

Nu=0,023·Re^0,8·Pr^0,4=0,023·24259,7^0,8·0,641^0,4 =62

ponieważ L<50d to:

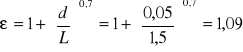
więc:

Nu=62·1,09=67,6

Wykres zależności Nu=f(Re):

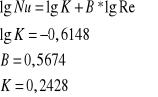
Równanie kryterialne ma zatem postać:

Błędy pomiędzy wartościami obliczonymi i doświadczalnymi obliczam ze wzorów:

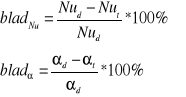
Nu			alfa
doś.	teor.	błąd	doś.	teor.	błąd
73,3	67,6	7,87	31,1	36,9	-18,7
71,1	61,9	12,9	29,2	33,8	-15,9
66	54,8	17,07	26,7	29,9	-12,1
58,3	49,1	15,81	24,6	26,8	-8,87
50,1	40,7	18,77	21,5	22,2	-3,44

Różnice pomiędzy wartościami teoretycznymi a doświadczalnymi są dość duże (do 20%) .

Konwekcja swobodna

Dane fizykochemiczne dla kondensatu dla temp otoczenia 25[^oC]

- gęstość kondensatu ρ_k=992 [kg/m³]

- ciepło kondensacji r=2406 [kJ/kg]

Obliczenie temperatury średniej:

Dane fizykochemiczne dla powietrza dla średniej temp t_śr=36,27 [^oC]

gęstość	lepkość	Ciepło właściwe	Przew. cieplne
ρ[kg/m^3]	[Pas]	Cw [J/kgK]	λ [W/mK]
1,775	1,578*10^-5	1005	0,0262

Obliczenie strumienia

Obliczenie wartości temperatury powierzchni osłony izolacji wymiennika z zależności:

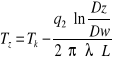
Dz - średnica zewnętrzna izolacji = 0,21 [m]

Dw - średnica wewnętrzna izolacji= 0,198 [m]

- strumień wymienionego ciepła [W]

T_k - temp. kondensatu [K]

- współczynnik przewodzenia ciepła dla izolacji = 0,16

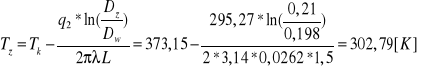
Obliczenie doświadczalnego współczynnika wnikania ciepła

q_iz-q_1-2=α·A_z·∆T

Obliczenie strumienia ciepła wymiany na drodze promieniowania

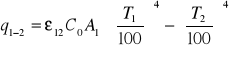
A₂>>A₁ to ε₁₂= ε₁=0,04

C₀ - techniczna stała promieniowania ciała doskonale czarnego

- stopień czarności ciała = 0,04

T₁ = T_iz = 322,58 [K]

T₂ - temperatura otoczenia = 296,25 [K]

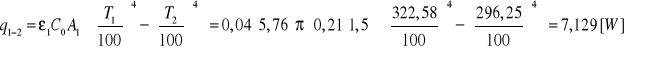
to

Obliczenie teoretycznego współczynnika wnikania ciepła

Obliczenie liczby Grashoffa:

Gr·Pr=4,78·10¹⁰·0,605=2,89·10¹⁰

Nu=0,135(Gr·Pr)^1/3=0,135·(2,89·10¹⁰)^1/3=414,45

[W/m²K]

WNIOSKI

Wyniku przeprowadzonych obserwacji i wykonanych obliczeń wynika, że współczynnik wnikania ciepła w konwekcji swobodnej jest kilkakrotnie mniejszy od współczynnika w konwekcji wymuszonej. Szybkość obrotów wentylatora (prędkość powietrza) ma znaczący wpływ na zjawisko, a mianowicie im wyższa szybkość obrotów wentylatora tym bardziej zauważalna jest intensyfikacja procesu. Niestety nie ostrzegliśmy się błędów pomiarów i to dość znaczących, nawet do 20%.

---