Sprawozdanie z ćwiczenia nr 2.

Nr. Ćwiczenia	Data	Imię i nazwisko	Wydział	Semestr	Grupa
2	04.12.12		Budownictwo	I	2 B
Temat: Wyznaczanie parametrów ruchu obrotowego bryły sztywnej.			Przygotowanie	Wykonanie	Ocena ostateczna

Cel ćwiczenia:

Celem ćwiczenia jest wyznaczenie parametrów ruchu obrotowego bryły sztywnej. Do przeprowadzenia tego ćwiczenie używamy wahadła Oberbecka. Do przymocowanego walca C przymocowane są 4 poziome pręty P, na których umieszczone są walce W, których odległość od środka można regulować. Na górnej części tego urządzenia nawinięta jest nić, która przechodzi przez krążek K, a na końcu nici umieszczony jest ciężarek(walec) o masie m

1. Część teoretyczna.

Druga zasada dynamiki dla ruchu obrotowego - Moment siły działającej na bryłę sztywną jest równy iloczynowi momentów bezwładności I tej bryły I jej przyspieszenia kątowego α.

Moment bezwładności - punkt materialnego A względem osi jest iloczyn masy tego punktu m i kwadratu jego odległości d od osi. Moment bezwładności ciała sztywnego jest miarą jego bezwładności w ruchu obrotowym, podobnie jak masa punktu materialnego jest miarą jego bezwładności w ruchu postępowym.

moment bezwładności danego ciała można wyrazić także wzorem

Twierdzenie Steinera - moment bezwładności I ciała względem dowolnej osi obrotu nie przechodzącej przez jego środek masy jest większy od momentu bezwładności I względem osi równoległej przechodzącej przez środek masy ciała o iloczyn masy ciała m i kwadratu odległości d między obiema osiami.

Moment siły - jeśli na ciało nie działa żaden moment siły to moment pedu tego ciała jest stały ( ciało obraca się ze stałą prędkością kątową ).

Użyte wzory w ćwiczeniu:

Moment ciężkości odważnika

Moment bezwładności walca względem jego osi

Moment bezwładności walca względem średnicy przechodzącej przez środek bryły

Moment bezwładności pręta względem osi prostopadłej do niego przechodzącej przez jego koniec

Moment bezwładności I₀

2. Rysunek do ćwiczenia.

3. Tabela pomiarowa.

1.Tabela pomiarowa dla masy walca W:

Wielkość	Wymiar	Pomiar 1	Pomiar 2	Pomiar 3
h	m	0,015	0,015	0,015
R	m	0,02	0,02	0,02
hśr	m	0,015
Rśr	m	0,02
d	m	0,04
Mw	kg	0,000050868
Mwr	kg
ρ	kg/m^3	2,7

2.Tabela pomiarowa dla walca C:

Wielkość	Wymiar	Pomiar 1	Pomiar 2	Pomiar 3
dc	m	0,03	0,03	0,03
lc	m	0,05	0,05	0,05
dcśr	m	0,03
lcśr	m	0,05
ρ	kg/m^3	2,7
Mc	kg	0,01933

3. Tabela pomiarowa dla pręta l:

Wielkość	Wymiar	Pręt 1	Pręt 2	Pręt 3	Pręt 4
l1	m	0,19	0,19	0,19	0,19
dl	m	0,006	0,006	0,006	0,006
llśr	m	0,19
dlśr	m	0,006
ρ	kg/m^3	2,7
Ml	kg

4.Tabela pomiarowa dla sprawdzenia równania ruchu:

Lp	Pomiary				Wyniki obliczeń
		Masa m	Liczba obrotów N	Czas spadania masy t	Odległość d mas od osi walca	Ic	Iw	Ip	I
		kg	-	s	m	kgm^2	kgm^2	kgm^2	kgm^2
1.	0,0923	5	7,14	0,05	0,3 *10^-9	0, 31175 *10^-4	0, 83664 *10^-6	0,0000315
2.	0,0923	5	9,05	0,08							0,010462
3.	0,0923	5	9,82	0,1							0,000033
4.	0,0923	5	10,97	0,12							0,00003388
5.	0,0923	5	13,53	0,15							0,0000355

5.Tabela dla obliczeń regresji liniowej

Wielkość	Wymiar	Wartość
d1	m	0,05
d2	m	0,08
d3	m	0,1
d4	m	0,12
d5	m	0,15
t^2	s^2	102,01
d^2	m^2	0,064
a	s^2/m^2	92,15
b	s^2	29
I	kg*m^2	0,000031

Wykres zależności między czasem a odległością mas od osi walca

4. Obliczenia.

Obliczam moment ciężkości działający na bryłę:

M = r_c × _Mc × g = 0,015 m × 0,1933 kg × 9,81 m/s² × sin 90°

M = 0,028 Nm

Obliczam moment bezwładności walca względem jego osi:

I_c = 1/2 MRw² = 0,5 × 0,028 Nm × 0,0000000025 m²

I_c = 0,00000000036 Nm³

Obliczam moment bezwładności walca:

I_w = M.(1/4 R² + 1/12 h²)

I_w = 0,028 Nm (0,25 × 0,00005 m² + 0,083 × 0,000225m²)

I_w = 0,0000311 Nm³

Obliczam moment bezwładności pręta:

I_p = 1/12M×d_l2 = 0,083 × 0,028 Nm × 0,000036 m²

I_p = 0,000000083 Nm³

Obliczam moment bezwładności I_o:

I_o = 0,00000000036 Nm³ + 0,000031175 Nm³ + 0,000000083664 Nm³

I_o = 0,000031 Nm³

Obliczam całkowity moment bezwładności dla pięciu położeń walca:

1. d₁ = 0,05 m

I₁ = I_o + 4 m_w × d²

I₁ = 0,000031 + 4 × 0,00005 × 0,0025 = 0,0000315 Nm³

2. d₂ = 0,08 m.

I₂ = I_o + 4 m_w × d²

I₂ = 0,000031 + 4 × 0,00005 × 0,0064 = 0,010462 Nm³

3. d₃ = 0,1 m.

I₃ = I_o + 4 m_w × d²

I₃ = 0,000031 + 4 × 0,00005 × 0,01 = 0,000033 Nm³

4. d₄ = 0,12 m.

I₄ = I_o + 4 m_w × d²

I₄ = 0,000031 + 4 × 0,00005 × 0,0144 = 0,00003388 Nm³

5. d₅ = 0,15 m.

I₅ = I_o + 4 m_w × d²

I₅ = 0,000031 + 4 × 0,00005 × 0,0225 = 0,0000355 Nm³

Stosując regresję liniową, obliczamy współczynnik nachylenia i punktu przecięcia z osią y , które to wielkości wykorzystujemy do wyznaczenia I_o.

X	0,0025	0,0064	0,01	0,0144	0,0225
Y	50,98	96,43	81,9	120,34	183,06

Σx = 0,0558

Σy = 532,71

Σxy = 29,73

(Σx)² = 0,00311

Σx² = 0,00155

gdzie:

y = ax + b

y = 92,15x + 9

Według regresji liniowej obliczam I_o i m_w oraz I :

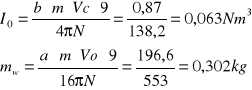
Dla wyników z regresji liniowej obliczam moment bezwładności walca oraz moment siły:

I	α	M. = I × α
I1 = 0,047	α = 0,4	M1 = 0,0199
I2 = 0,026	α = 0,77	M2 = 0,02
I3 = 0,018	α = 1,04	M3 = 0,019
I4 = 0,011	α = 1,9	M4 = 0,021
I5 = 0,0075	α = 3,6	M5 = 0,025

Wyniki:

	Obliczenia teoretyczne.	Obliczenia według regresji liniowej
M.	0,028 Nm	0,021 Nm
Io	0,000031 Nm^3	0,0063 Nm^3
I1	0,0000315 Nm^3	0,047 Nm^3
I2	0,010462 Nm^3	0,026 Nm^3
I3	0,000033 Nm^3	0,018 Nm^3
I4	0,00003388Nm^3	0,011 Nm^3
I5	0,0000355Nm^3	0,0075 Nm^3
mw	0,00005 kg	0,302 kgNm^3

5. Wnioski.

Badając parametry ruchu obrotowego bryły sztywnej wnioskujemy iż im bliżej ustawiliśmy walce W na ramionach tym mniejszy okazywał się całkowity moment bezwładności I i jednocześnie zmniejszał się moment pędu M, oraz ciężarek opadający szybciej pokonywał odcinek 0,5m.

4