OPTYKA

Prawo odbicia światła:

Gdy światło pada na granicę dwóch ośrodków, to ulega odbiciu zgodnie z prawem odbicia, które mówi, że jeśli kąt padania i kąt odbicia leżą w jednej płaszczyźnie, to kąt padania jest równy kątowi odbicia: α=β.

Dzięki zjawisku odbicia widzimy nasze otoczenie. Wszystkie przedmioty odbijają światło, które trafia do naszych oczu z informacją o wyglądzie tych ciał.

Prawo załamania światła:

Zmiana kierunku promieni świetlnych podczas załamania nie jest przypadkowa. Opisuje to prawo załamania światła nazywane niekiedy prawem Snelliusa.

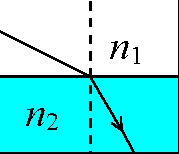
Prawo załamania światła łączy ze sobą dwa kąty - kąt padania na powierzchnię rozgraniczającą dwa ośrodki i kąt załamania powstający gdy promień przejdzie granicę i zacznie się rozchodzić w drugim ośrodku (patrz rysunek niżej).

Warto zwrócić uwagę na fakt, że kąty padania i załamania są liczone odnormalnej do powierzchni, a nie od samej powierzchni.

Prawo załamania - postać 1 - podstawowa

		α - kąt padania β - kąt załamania v1 - prędkość światła w ośrodku 1 v2 - prędkość światła w ośrodku 2
Słownie prawo załamania można sformułować następująco: Stosunek sinusa kąta padania, do sinusa kąta załamania jest dla danych ośrodków stały i równy stosunkowi prędkości fali w ośrodku pierwszym, do prędkości fali w ośrodku drugim. Kąty padania i załamania leżą w tej samej płaszczyźnie. Inne postacie prawa załamania Zdefiniujmy wielkość zwaną bezwzględnym współczynnikiem załamania ośrodka:
	v - prędkość światła w ośrodku c - prędkość światła w próżni (c = 299 792 458 m/s) n - bezwzględny współczynnik załamania
Podstawmy teraz tę wielkość do wzoru na prawo załamania, zmieniając nieco postać - tzn. wyliczając prędkość v (wzór otrzymujemy mnożąc obie strony ostatniego równania przez v i dzieląc przez n):
Podstawimy ten wzór raz w wersji dla ośrodka 1  (n1 - bezwzględny współczynnik załamania w ośrodku 1)    A potem w wersji dla ośrodka 2  (n2 - bezwzględny współczynnik załamania w ośrodku 2)

Wtedy otrzymamy:
		n1 - bezwzględny współczynnik załamania ośrodka 1 n2 - bezwzględny współczynnik załamania ośrodka 2 c - prędkość światła w próżni
Stąd ostatecznie będziemy mieli drugą postać prawa załamania światła. Wzór prawa załamania - postać 2    Ta wersja prawa załamania wiąże kąty padania i załamania z bezwzględnymi współczynnikami załamania w obu ośrodkach. Sformułowanie słowne: Stosunek sinusa kąta padania, do sinusa kąta załamania jest równy stosunkowi bezwzględnego współczynnika załamania ośrodka do którego przechodzi fala, do bezwzględnego współczynnika załamania ośrodka, z którego fala pada na powierzchnię rozgraniczającą oba ośrodki. Wzór prawa załamania - postać 3 Jest jeszcze trzecia postać prawa załamania. Powstaje ona po zdefiniowaniu kolejnej wielkości zwanej względnym współczynnikiem załamania:
		n1 - bezwzględny współczynnik załamania ośrodka 1 n2 - bezwzględny współczynnik załamania ośrodka 2 n12 - współczynnik załamania (względny) ośrodka 2 względem ośrodka 1
Warto zwrócić uwagę na fakt, że względny współczynnik załamania czyta się od tyłu: - jest to współczynnik załamania ośrodka drugiego (do którego wchodzi światło) względem ośrodka pierwszego (z którego przychodzi światło). Po podstawieniu względnego współczynnika załamania do 2 postaci prawa załamania otrzymamy: Zatem:   stosunek sinusa kąta padania do sinusa kąta załamania jest równy względnemu współczynnikowi załamania światła ośrodka do którego światło wpada względem ośrodka z którego światło wychodzi.

Bezwzględny i względny współczynnik załamania światła:

Bezwzględny współczynnik załamania światła

Bezwzględny współczynnik załamania światła dany jest wzorem 

v - prędkość światła w danym ośrodku
c - prędkość światła w próżni (c = 299 792 458 m/s)
n - bezwzględny współczynnik załamania

Znajomość bezwzględnych współczynników załamania umożliwia szybkie obliczenie prędkości światła w danych ośrodku, wg wzoru:

  

Przykład:

Prędkość światła w szkle wynosi ok. 2/3 prędkości światła w próżni. Współczynnik załamania szkła wynosi więc 3/2 - 1,5.

Względny współczynnik załamania światła

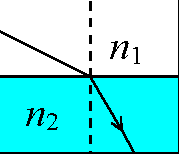
Mając bezwzględne współczynniki załamania ośrodka z którego pada światło i ośrodka do którego załamuje się światło, można obliczyć względny współczynnik załamania (patrz prawo załamania światła):

n₁ - bezwzględny współczynnik załamania ośrodka 1 (z którego wychodzi światło)

n₂ - bezwzględny współczynnik załamania ośrodka 2 
(do którego przechodzi światło)

n₁₂ - współczynnik załamania (względny) ośrodka 2 względem ośrodka 1

Względny współczynnik załamania decyduje o tym jak bardzo światło ma tendencję do skręcania swego kierunku podczas przechodzenia do innego ośrodka. Inaczej mówiąc -  przy dużym względnym współczynniku załamania światło będzie się silniej załamywać.

W przypadku, gdy nie ma dokładnego stwierdzenia o jaki współczynnik chodzi, najczęściej samo wyrażenie "współczynnik załamania" należy rozumieć jako "bezwzględny współczynnik załamania".

Dualizm korpuskularno-falowy:

Dualizm korpuskularno-falowy cecha wielu obiektów fizycznych polegająca na tym, że w pewnych sytuacjach zachowują się one, jakby były cząstkami (korpuskułami), a w innych sytuacjach, jakby były falami 
O falowej naturze światła świadczą zjawiska dyfrakcja i interferencja światła. O korpuskularnej naturze świadczy zjawisko fotoelektryczne zewnętrzne, efekt Comptona.

Zjawisko Comptona polega na rozproszeniu promieniowania rentgenowskiego na swobodnych elektronach. Promieniowanie rozproszone ma większą długość fali niż promieniowanie padające. Ma tu miejsce sprężyste zderzenie fotonu i elektronu.

Zjawisko fotoelektryczne zewnętrzne polega na wybijaniu elektronów z powierzchni metalu przez promieniowanie elektromagnetyczne.

Światło jako fala elektromagnetyczna:

Drgające ładunki elektryczne wytwarzają w przestrzeni zmienne pole elektryczne, które zgodnie z prawem Maxwella indukuje zmienne pole magnetyczne, a to z kolei indukuje zmienne pole elektryczne itd. Tak więc drgania pola elektrycznego wzbudzają drgania pola magnetycznego i odwrotnie. 
Drgające pola, które wzajemnie się wzbudzają, nazywamy promieniowaniem elektromagnetycznym. Promieniowanie elektromagnetyczne rozchodzi się w przestrzeni jak fala o częstotliwości równej częstotliwości drgań ładunku elektrycznego, który jest jej źródłem, i dlatego promieniowanie to nazywamy falą elektromagnetyczną.

Wszystkie znane nam fale elektromagnetyczne mają częstotliwości, które mieszczą się w przedziale od 10 do 3-ej Hz (długie fale radiowe) do 10 do 22-ej Hz (promieniowanie gamma) i tworzą widmo promieniowania elektromagnetycznego. Światło widzialne, czyli to, które rejestrują nasze oczy, to mały fragment całego widma fal elektromagnetycznych. Podlega ono tym samym prawom, jakim podlegają fale elektromagnetyczne. W danym ośrodku wszystkie fale elektromagnetyczne rozchodzą się z taką samą prędkością, która w próżni wynosi 3 · 10 do 8-ej m/s.

SOCZEWKI

Rodzaje soczewek i ich własności:

Konstrukcja obrazów w soczewkach skupiających i rozpraszających:

Ogniskowa soczewki, promień krzywizny soczewki:

Równania soczewkowe:

Zdolność skupiająca soczewki:

Zdolność skupiająca soczewki jest odwrotnością jej ogniskowej wyrażonej w metrach:

Gdy f > 0, to Z > 0 i soczewka jest skupiająca, a gdy f < 0, to Z < 0 i soczewka jest rozpraszająca.

Zdolność skupiającą soczewki można wyrazić poprzez promienie jej krzywizn oraz współczynnik załamania materiału soczewki względem ośrodka, w którym jest soczewka

Wykorzystując powyższy wzór należy uwzględnić, że jeśli powierzchnia ograniczająca soczewkę jest wypukła, to jej promień krzywizny jest dodatni, jeśli powierzchnia jest wklęsła, to jej promień krzywizny jest ujemny. Dla soczewek ograniczonych z jednej strony płaszczyzną (płasko-wypukłych lub płasko-wklęsłych) jeden z promieni krzywizn jest nieskończenie duży i dlatego odwrotność takiego promienia wynosi zero. W takim przypadku:

Obydwa wzory pozwalają zauważyć, że dla soczewek wypukłych zdolność skupiająca jest dodatnia, jeśli n_2/1>1. Soczewki wklęsłe mają w tym przepadku ujemną zdolność skupiającą i rozpraszają światło. Jest tak na przykład dla szklanej soczewki w powietrzu, dla której n_2/1 = 1,52 > 1. Jeśli jednak mamy soczewkę np. w postaci pęcherzyka wody w szkle, to wtedy współczynnik załamania wody względem szkła n_2/1 < 1 i wówczas soczewka wklęsła jest skupiająca, a wypukła jest rozpraszająca.

ELEKTRYCZNOŚĆ

Prąd stały i prąd zmienny:

Prąd stały charakteryzuje się stałymi wartością natężenia oraz kierunkiem przepływu. Większość układów elektronicznych zasilana jest prądem stałym. Mogą być zasilane bezpośrednio z baterii lub akumulatorów. Dla urządzeń, które są zasilane z sieci energetycznej stosuje się zasilanie prądem stałym wytwarzanym przez zasilacze sieciowe.

Prąd zmienny to prąd elektryczny, którego wartość natężenia zmienia się w czasie. Prąd zmienny nieokresowy może reprezentować prąd o dowolnej zmienności w czasie (czarna krzywa na rysunku), może też prąd zmieniający się zgodnie z określoną funkcją matematyczną lub w sposób zdeterminowany zjawiskiem fizycznym. Potocznie termin prąd zmienny stosowany jest często do prądu okresowego o przebiegu sinusoidalnym.

Natężenie i napięcie prądu:

Natężenie prądu jest wielkością podstawową, definiowaną jako stosunek ładunku przepływającego przez przekrój poprzeczny przewodnika do czasu w jakim on przepłynął.

I  - natężenie prądu (w układzie SI w amperach - A)
q  - przenoszony ładunek (w układzie SI w kulombach - C)
t  - czas (w układzie SI w sekundach - s)

Jeden amper odpowiada prądowi przenoszącemu w ciągu jednej sekundy ładunek jednego kulomba.

Jeden amper, to 1 kulomb na sekundę:

Napięcie jest różnicą potencjałów między dwoma punktami obwodu (układu).

Napięcie (podobnie jak sam potencjał) w układzie SI mierzymy w woltach (V).

  

Napięcie różne od zera może występować tylko między dwoma istotnie różnymi (przedzielonymi jakimś źródłem, lub odbiornikiem prądu) punktami obwodu.

Przykładowo, jeżeli potencjał jednego punktu wynosi V₁ = 5 V, a potencjał drugiego V₂ = 12 V, to między tymi punktami panuje napięcie między tymi punktami ma wartość

U = 12 V - 5 V = 7 V

Przepływ prądu w obwodzie elektrycznym:

Warunki trwałego przepływu prądu:
a) zamknięta droga dla przepływu ładunków. Drogę taką nazywamy obwodem elektrycznym.
b) obecność źródła energii elektrycznej, które zmusza ładunki do poruszania się.
W skład obwodu elektrycznego wchodzą:
a) źródła energii (nazywamy je elementami czynnymi)
b) odbiorniki (tzw. elementy bierne, pasywne)
c) przewody łączące.
Źródła energii elektrycznej to urządzenia przetwarzające różne rodzaje energii na energię elektryczną. Mają dwa bieguny (zaciski, elektrody) między którymi istnieje różnica potencjałów nazywana napięciem źródłowym lub siłą elektromotoryczną (SEM)
Odbiorniki -przetwarzają energię elektryczną na inne rodzaje energii (np.: świetlną, cieplną)

Podłączanie amperomierza i woltomierza do obwodów elektrycznych:

Pomiar natężeń prądu: 
Do pomiaru natężenia prądu służą amperomierze (miliamperomierze, mikroamperomierze). Aby zmierzyć natężenie prądu I płynącego przez przewodnik o oporze R należy dołączyć do niego szeregowo amperomierz ponieważ przy łączeniu szeregowym prąd o takim samym natężeniu przepływa przez przewodnik i przez amperomierz. Włączenie amperomierza nie powinno powodować zmiany natężenia prądu i płynącego w obwodzie, dlatego opór amperomierza R1 powinien być mały w porównaniu z innymi oporami w obwodzie. Idealny amperomierz powinien mieć opór elektryczny równy zeru. 

Pomiar napięć prądu: 
Do pomiaru napięć służą woltomierze (miliwoltomierze). W celu wyznaczenia napięcia na końcach przewodnika o oporze R należy woltomierz dołączyć do opornika równolegle. Podłączenie równoległe woltomierza do przewodnika nie powinno powodować zmiany natężenia prądu płynącego przez ten opornik. Ponieważ następuje rozgałęzienie prądu więc część prądu o natężeniu Ir popłynie przez woltomierz, a przez opornik prąd o natężeniu IR, gdzie IR=I-Ir. 
Ważne jest by przez woltomierz popłynął prąd Ir o jak najmniejszym natężeniu, dlatego opór woltomierza Rv powinien być bardzo duży w stosunku do oporu opornika R na którym jest mierzone napięcie (Rv>>R), dlatego że Ir/IR=R/Rv 
Idealny woltomierz powinien mieć opór nieskończenie duży. 

PRAWO OHMA

Opór elektryczny, przyczyny jego powstawania:

Opór elektryczny związany jest z zaburzeniem swobodnego przepływu prądu w przewodniku.

Czynnikiem zaburzającym ten ruch w metalach są zderzenia elektronów z drgającymi jonami sieci krystalicznej. Opór elektryczny jest oznaczany literą R, a jego jednostką jest om [Ω].

Wartość oporu można obliczyć ze wzoru:


gdzie: ρ jest oporem właściwym, jego wartość zależy od rodzaju materiału, l - długość przewodnika, S - pole przekroju poprzecznego.

Prawo Ohma:

Prawo Ohma mówi, że napięcie U na końcach przewodnika, przez który płynie prąd o natężeniu I jest iloczynem natężenia prądu i rezystancji R tego przewodnika, czyli

Opór właściwy, przewodnictwo:

Rezystywność (oporność właściwa, opór właściwy) - wielkość charakteryzująca przewodnictwo elektryczne materiału. Jej wartość jest różna dla różnych materiałów.

Rezystywność jest zazwyczaj oznaczana jako ρ (mała grecka litera rho).

W przypadku jednorodnego materiału izotropowego rezystywność określa zależność rezystancji (oporu) materiału od jego wymiarów:

Z czego wynika:

,

gdzie: R - rezystancja (opór), S - pole przekroju poprzecznego elementu, l - długość elementu.

Jednostką rezystywności w układzie SI jest om⋅metr (Ω·m).

Odwrotność rezystywności to konduktywność.

Ze względu na opór właściwy ciała dzieli się na następujące grupy:

• metale, będące bardzo dobrymi przewodnikami (opór właściwy rzędu 10⁻⁸ Ω·m),

• półprzewodniki (10⁻⁶ Ω·m),

• izolatory (10¹⁰ - 10¹⁶ Ω·m).

Granice te są umowne, w różnych dziedzinach techniki i fizyki używa się różnych.

Zależność oporu od parametrów geometrycznych i temperatury:

Wartość oporu zależy także od temperatury przewodnika. Wraz ze wzrostem temperatury rośnie energia drgań jonów dodatnich, co powoduje silniejsze zaburzenie swobodnego przepływu elektronów. Opór przewodników rośnie więc wraz ze wzrostem temperatury.

Wartość oporu zależy od długości przewodnika (im dłuższy przewodnik, tym większy opór), pola przekroju poprzecznego (większe pole - mniejszy opór) oraz od rodzaju materiału, z którego wykonany jest przewodnik.

I prawo Kirchhoffa:

Pierwsze prawo Kirchhoffa mówi, że suma prądów wpływających do węzła jest równa sumie prądów wypływających z niego lub inaczej, że suma wszystkich prądów w węźle jest równa zeru (patrz rysunek powyżej).

Prądy wpływające do węzła mają znak dodatni, a wypływające znak ujemny. Przykładem węzła jest punkt A na rysunku. Prądy I1, I2 są dodatnie, a I3 ujemny.

II prawo Kirchhoffa:

Drugie prawo Kirchhoffa mówi, że w obwodzie zamkniętym (oczku) suma wszystkich napięć jest równa zeru.

Napięcia, których zwrot strzałki jest zgodny z obiegiem oczka są dodatnie, a te, których zwrot jest przeciwny są ujemne. Obieg oczka przyjmuje się zgodnie z zaznaczoną okrągłą strzałką wewnątrz obwodu. Zgodnie z tymi założeniami napięcia U1 i U4 są dodatnie, a U2 i U3 ujemne.

Łączenie równoległe i szeregowe oporników:

1. Szeregowe połączenie oporów

Opory są połączone w szereg, gdy koniec jednego połączony jest z początkiem następnego. Opór zastępczy tego układu czyli taki pojedynczy opór, który wprowadzony do obwodu zamiast oporników połączonych szeregowo nie spowodowałby zmiany natężenia i napięcia można obliczyć wychodząc od drugiego prawa Kirchhoffa.

I tak dla układu trzech oporników prawo to ma postać:

E = I (R1 + R2 + R3 + Rw)

Czyli w przypadku szeregowego połączenia oporników całkowity opór zewnętrzny jest sumą połączonych oporów.

Rc = R1 + R2 + R3

2. Równoległe łączenie oporów

Opory są połączone równolegle wtedy, gdy dołączona jest do nich ta sama różnica potencjałów. W celu obliczenia oporu zastępczego dla tego układu należy najpierw znaleźć całkowite natężenie prądu (z I prawa Kirchhoffa).

I = I1 + I2 + I3

A ponieważ 

Zatem całkowity opór obwodu będzie równy: 

Porównując zależności na opór zastępczy dla połączenia szeregowego i równoległego widać, że opór zastępczy połączenia równoległego jest mniejszy od każdego z oporów tworzących to połączenie. Natomiast w przypadku połączenia szeregowego opór zastępczy jest większy od każdego z oporów składowych.

Połączenie równoległe oporników jest bardziej praktyczne od połączenia szeregowego. Zdecydowanym minusem połączeń szeregowych jest sumowanie się napięć. Może to łatwo doprowadzić do przeciążenia obwodu, w razie przyłączenia jednocześnie zbyt wielu oporników. Poza tym w razie uszkodzenia jednego z nich prąd w układzie przestaje płynąć.

W przypadku połączeń równoległych napięcia nie sumują się, nie ma więc ryzyka przerwania obwodu.

---