EKONOMETRIA I PROGNOZOWANIE PROCESÓW EKONOMICZNYCH - ĆWICZENIA

Ćwiczenia z dnia 27.04.2014 r.

Zad.1

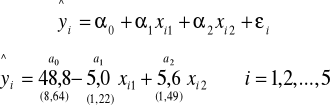
Pkt. A)

Znak minus oceny a₁ jest poprawny gdyż wraz z wydłużaniem się stażu pracy pracownika, ilość wytwarzanych przez niego braków maleje.

Znak plus oceny a₂ jest poprawny, gdyż wraz ze wzrostem liczby dni przepracowanych w warunkach szkodliwych dla zdrowia , rośnie liczba braków wytwarzanych przez pracownika.

Jeżeli staż pracy wzrośnie o rok to liczba wytwarzanych przez niego braków zmaleje o 5 sztuk rocznie przy założeniu, że liczba dni przepracowanych w warunkach szkodliwych dla zdrowia nie ulegnie zmianie.

Jeżeli liczba dni przepracowanych w warunkach szkodliwych dla zdrowia wzrośnie o 1 dzień w miesiącu to liczba braków wytwarzanych przez pracownika wzrośnie o 5,6 szt./rok przy założeniu, że jego staż pracy nie ulegnie zmianie.

W przypadku pracownika, który nie przepracował pełnego roku i nie pracuje w warunkach szkodliwych dla zdrowia, liczba wytworzonych przez niego braków wynosi około 49 sztuk.

• Budujemy macierz

• Gdy oznaczymy
  

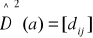
1. Średni błąd oceny a₀ parametru d₀
   

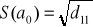
2. Średni błąd oceny a₁ parametru d₁
   

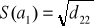
3. Średni błąd oceny a₂ parametru d₂
   

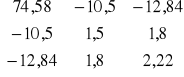
Pkt. B)

Badanie istotności zmiennych w modelu

Czy dana zmienna istotnie wpływa na główną zmienną ?

y = ax + b

a = 0

a ≠ 0

Istotność zmiennej x_j badamy stosując test istotności t- Studenta

• Formułujemy hipotezy

H₀ :
_j = 0

H₁ :
_j ≠ 0

• Ustalamy poziom istotności testu
  

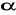
• Sprawdzianem hipotezy H₀ (przy założeniu, n
  ~
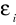
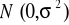
  prawdziwości H₀) jest statystyka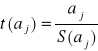
  o rozkładzie t - Studenta (dla ustalonego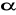
  i liczby stopni swobody równym n - (k+1)

• Wyznaczamy zbiór krytyczny

gdzie:

• 
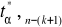
  jest wartością krytyczną odczytaną z tablic rozkładu t - Studenta dla ustalonego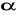
  i liczby stopni swobody równej n-(k+1)

• Obliczamy wartość statystyki t (a_j)

• Decyzje w teście :

Jeżeli t (a_j) = Z, to odrzucamy hipotezę H₀ (na poziomie istotności
) na rzecz hipotezy H₁ ; zmienna x_j jest istotna, jeżeli t (a_j)
Z , to nie ma podstaw do odrzucenia H₀ (na poziomie istotności
).

Zmienna x_j jest nie istotna

Istotność zmiennej X₁

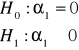
• Ustalamy poziom istotności testu
  

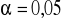
• Sprawdzianem hipotezy H₀ jest statystyka
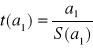
  o rozkładzie t - Studenta dla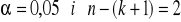
  

Obliczamy wartość krytyczną

Ponieważ t (a₁)= -4,098
Z = (-∞ , -4,303)
(4,303 , +∞) to nie ma podstaw do odrzucenia H₀ (na poziomie istotności
)

Zmienna X₁ jest nieistotna

Istotność zmiennej X₂

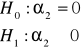
• Ustalamy poziom istotności testu
  

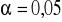
• Zbiór krytyczny

Ponieważ t (a₂)= 3,76
Z = (-∞ , -4,303)
(4,303 , +∞) to nie ma podstaw do odrzucenia H₀ (na poziomie istotności
)

Zmienna X₂ jest nieistotna

Pkt. C)

• Prognozowanie na podstawie modelu opisowego

• Znany jest wektor wartości zmiennych objaśniających w okresie
  

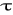
Wartość prognozowana zmiennej y jest wartością

Średni błąd predykcji ex ante

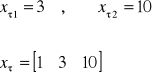
• Wartość prognozowana zmiennej y

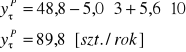
W oparciu o szacowany model przewiduje się, że pracownik z 3-letnim stażem, który w miesiącu pracuje 10 dni w warunkach szkodliwych dla zdrowia, wytwarza około 90 braków rocznie.

Średni błąd predykcji ex ante

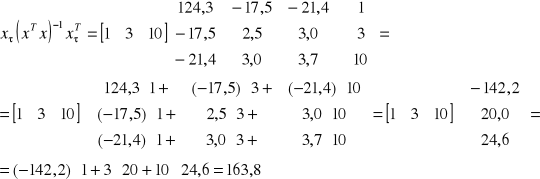
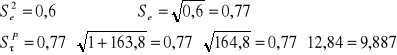
Zad.2

Autokorelacja składnika losowego

Schemat autokorelacji I rzędu AC (I)

Gdzie:

- współczynnik autokorelacji

- pewna zmienna losowa
~

gdzie

Wartość estymatora współczynnika autokorelacji
obliczamy stosując wzór :

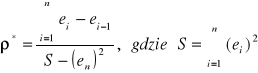
Test Durbina -Watsona

• W zależności od znaku
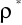
  testujemy hipotezy :

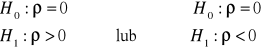
• Sprawdzianem hipotezy H₀ jest statystyka

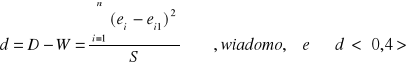
• Ustalamy poziom istotności
  

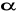
Odczytujemy z tablic wartości krytycznych D-W dwie wartości krytyczne:

• Obliczamy wartość d* statystyka D-W

d^* = 1,7197

nie występuje autokorelacja składnika losowego

---