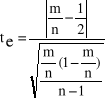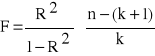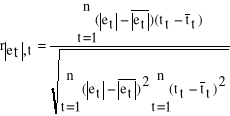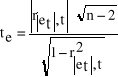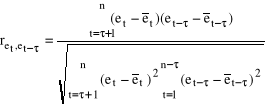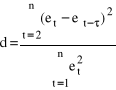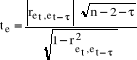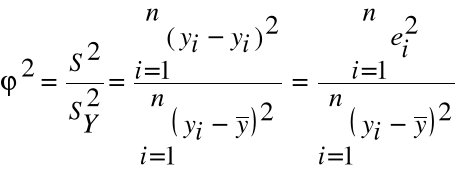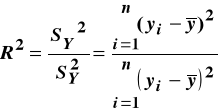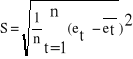KLASYCZNA METODA NAJMNIEJSZYCH KWADRATÓW. ESTYMACJA MODELI Z WIELOMA ZMIENNYMI OBJAŚNIAJACYMI. WERYFIKACJA MODELI Klasyczna Metoda Najmniejszych Kwadratów (KMNK) służy do estymacji parametrów strukturalnych modeli liniowych jednorównaniowych i wielorównaniowych prostych i rekurencyjnych (z jedną i wieloma zmiennymi objaśniającymi). Idea klasycznej metody najmniejszych kwadratów jest następująca: należy ustalić takie wartości ocen parametrów strukturalnych, dla których suma kwadratów odchyleń wartości empirycznych zmiennej objaśnianej od jej wartości teoretycznych wynika­jących z modelu: , jest minimalna, czyli: , przy czym , oznacza, że parametr jest ukrytym wyrazem wolnym, a k jest liczbą zmiennych objaśniających. ZAŁOŻENIA KLASYCZNEJ METODY NAJMNIEJSZYCH KWADRATÓW - KMNK Model jest niezmienniczy ze względu na obserwacje. Zakłada się stabilność relacji występujących między badanymi zmiennymi. Postać modelu jest liniowa lub sprowadzalna do liniowej względem parametrów. Zmienne objaśniające są nielosowe. Zmienne objaśniające są wolne od współliniowości. Żadna ze zmiennych objaśniających nie może stanowić kombinacji liniowej pozostałych. Formalnie można to zapisać: r (X) = k + 1 gdzie: X - macierz obserwacji na zmiennych objaśniających r (X) - rząd macierzy X k - liczba zmiennych objaśniających Liczba obserwacji musi być większa od liczby zmiennych objaśniających więcej niż o 1 (n > k + 1) Składnik losowy ma rozkład normalny. Składnik losowy ma wartość oczekiwaną równą 0. Składnik losowy jest sferyczny tzn.: nie występuje autokorelacja składników losowych, czyli składniki losowe pochodzące z różnych okresów nie są wzajemnie zależne (skorelowane), jest homoskedastyczny , czyli ma stałą (nie zmieniającą się w czasie) wariancję o skończonej wartości. Składnik losowy nie jest skorelowany z żadną ze zmiennych objaśniających. Estymatorem parametrów strukturalnych uzyskanych za pomocą klasycznej metody najmniejszych kwadratów jest: , pod warunkiem, że macierz jest nieosobliwa. W zapisie macierzowym przyjmujemy następujące oznaczenia: b - wektor kolumnowy ocen parametrów strukturalnych o wymiarach (k+1)1, Y - wektor kolumnowy obserwacji na zmiennej objaśnianej o wymiarach (n1), X - macierz obserwacji na zmiennych objaśniających o wymiarach n(k+1). Estymatorem wariancji składnika losowego jest wariancja resztowa: Natomiast pierwiastek kwadratowy z wariancji resztowej, to standardowy błąd oceny: . Standardowy błąd oceny informuje o przeciętnych odchyleniach wartości empirycznych zmiennej objaśnianej od jej wartości teoretycznych , czyli wyliczonych z modelu. Błędy średnie ocen parametrów strukturalnych można oszacować na podstawie macierzy wariancji i kowariancji ocen parametrów strukturalnych D^2(b). Na głównej przekątnej tej macierzy znajdują się wariancje ocen parametrów strukturalnych, a ich pierwiastki - są błędami średnimi ocen parametrów strukturalnych. D^2(b) = S^2(X^TX)^-1 Błąd średni oceny informuje, o ile mogłaby się wahać ocena parametru strukturalnego, gdybyśmy mogli pobrać inną próbę o tej samej liczebności. Badanie symetrii rozkładu elementu losowego Cel: sprawdzenie poprawności doboru postaci analitycznej modelu. Badanie to przeprowadza się dla wszystkich modeli przy założeniach: dla modeli nieliniowych sprowadzalnych do liniowych dla postaci pierwotnej modelu, dla modeli segmentowych, dla całego zbioru segmentów łącznie. Jeżeli rozkład elementu losowego okaże się niesymetryczny należy wrócić do etapu II i dokonać ponownego wyboru postaci analitycznej. W celu sprawdzenia symetrii rozkładu elementu losowego weryfikujemy hipotezy: H0 : - element losowy ma rozkład symetryczny H1 : - element losowy nie ma rozkładu symetrycznego m - liczba reszt jednego znaku (dodatnich lub ujemnych). Reszty równe zero w badaniu pomijamy. Badanie symetrii za pomocą testu symetrii: Jeżeli m1 ≤ m ≤ m2 - nie ma podstaw do odrzucenia hipotezy zerowej, można przyjąć, że element losowy ma rozkład symetryczny Jeżeli m1 > m > m2 - odrzucamy hipotezę zerową na rzecz hipotezy H1, co oznacza, że element losowy nie ma rozkładu symetrycznego. Gdzie: m - liczba reszt dodatnich lub ujemnych (reszty równe 0 pomijamy), m1, m2 - wartość odczytana z tablic do testu symetrii dla poziomu istotności α = 0,1 i n obserwacji. Jeżeli reszty przyjmują tylko wartości „-” lub „+”, wówczas bez korzystania z tablic statystycznych można stwierdzić, że rozkład elementu losowego nie jest symetryczny. Rozkład elementu losowego jest symetryczny, gdy występuje dokładnie tyle samo reszt „-” i „+”. Badanie symetrii za pomocą testu t - Studenta (tylko dla małej próby): Należy wyznaczyć statystykę empiryczną: Statystykę teoretyczną odczytuje się z tablic rozkładu t - Studenta, dla zadanego poziomu istotności α i n - 1 stopni swobody. Jeżeli: te ≤ tt nie ma podstaw do odrzucenia hipotezy zerowej H0, czyli rozkład reszt jest symetryczny, te > tt należy odrzucić hipotezę zerową H0, na rzecz hipotezy alternatywnej - rozkład reszt nie jest symetryczny. Badanie losowości rozkładu elementu losowego Cel: sprawdzenie poprawności doboru postaci analitycznej modelu. Badanie losowości wymaga sztywnego uporządkowania obserwacji, dlatego przeprowadza się je dla modeli: zbudowanych w oparciu o szeregi czasowe danych, w porządku wg kolejnych okresów czasu, zbudowanych w oparciu o przekrojowe szeregi danych, z tym że: a/ dla modeli z jedną zmienną objaśniającą obserwacje należy uporządkować wg rosnących wartości tej zmiennej objaśniającej, b/ dla modeli z wieloma zmiennymi objaśniającymi porządkujemy obserwacje wg rosnących wartości wybranej zmiennej objaśniającej. Jeżeli rozkład elementu losowego nie jest losowy należy wrócić do etapu II i dokonać ponownego doboru postaci analitycznej modelu. Sprawdzenie losowości rozkładu elementu losowego: 1. Stawiamy hipotezy: H0 - składnik losowy ma rozkład losowy H1 - składnik losowy nie ma rozkładu losowego 2. Zakładamy, że: et > 0 → A et < 0 → B reszt równych 0 nie uwzględnia się, seria - ciąg następujących po sobie reszt oznaczonych jednakowym symbolem, czyli reszt o tym samym znaku, długość serii - liczba elementów, z których składa się seria. Test max. długości serii ke - maksymalna długość serii, kt - wartość odczytana z tablicy do „testu maksymalnej długości serii” dla poziomu istotności α = 0,05 i n obserwacji, Jeżeli ke ≤ kt - nie ma podstaw do odrzucenia hipotezy zerowej; rozkład elementu jest losowy; postać modelu jest poprawna. Jeżeli ke > kt - odrzucamy hipotezę zerową na rzecz H1; rozkład elementu nie jest losowy; postać modelu jest niewłaściwa. Test liczby serii ke - liczba serii, k1 - wartość odczytana z tablicy do „testu liczby serii” (lewostronnego) dla poziomu istotności α, i n1 reszt o jednym znaku i n2 reszt o drugim znaku, k2 - wartość odczytana z tablicy do „testu liczby serii” (prawostronnego) dla poziomu istotności 1 - α, i n1 reszt o jednym znaku i n2 reszt o drugim znaku. Jeżeli k1 ≤ ke ≤ k2 - nie ma podstaw do odrzucenia hipotezy zerowej, można przyjąć, że element losowy ma rozkład losowy. Jeżeli k1 > ke > k2 - odrzucamy hipotezę zerową na rzecz hipotezy H1, co oznacza, że element losowy nie ma rozkładu losowego : Istotność parametrów strukturalnych modelu Cel: Istotność parametrów strukturalnych modelu sprawdzamy w celu skontrolowania, czy do modelu weszły zmienne, które mają istotny wpływ na zmienną objaśnianą. Do badania istotności parametrów strukturalnych konieczne jest założenie, że element losowy ma rozkład normalny. Warunki przeprowadzenia badania istotności parametrów strukturalnych: nie sprawdzamy dla modeli adaptacyjnych (przystosowawczych), dla modeli nieliniowych sprowadzalnych do liniowych istotność parametrów sprawdza się dla postaci transformowanej (liniowej), istotności wyrazu wolnego nie bada się. Najbardziej ogólnym testem statystycznym sprawdzającym istotność parametrów strukturalnych modelu jest test F Fishera - Snedecora, za pomocą którego kontrolujemy, czy przynajmniej jeden parametr strukturalny w sposób istotny różni się od zera. W tym celu należy sformułować hipotezy: H0 : b1 = b2 = .... = bk = 0 H1 : b1 ≠ 0 ∨ b2 ≠ 0 ∨ ...∨ bk≠0 Sprawdzianem hipotez jest statystyka F. Statystyka ta ma rozkład F Fishera - Snedecora o m1 = k (liczba zmiennych objaśniających) oraz m2= n - (k +1) stopniach swobody. Statystykę teoretyczną F^* odczytujemy z tablic do testu F Fishera - Snedecora dla zadanego poziomu istotności α oraz m1 i m2 stopni swobody. W przypadku gdy: F ≤ F^* - brak podstaw do odrzucenia H0, co oznacza, że wszystkie parametry strukturalne modelu w sposób nieistotny różnią się od zera, czyli procedurę budowy modelu trzeba rozpocząć od początku, ponieważ należy usunąć wszystkie zmienne objaśniające modelu. F > F^* - należy odrzucić H0 na rzecz H1, co oznacza, że przynajmniej jeden z parametrów strukturalnych modelu w sposób istotny różni się od zera. Jeżeli w wyniku weryfikacji testu Fishera - Snedecora okazało się, że przynajmniej jeden parametr strukturalny modelu jest istotnie różny od zera, wówczas należy sprawdzić istotność wszystkich parametrów strukturalnych modelu (istotności wyrazu wolnego nie bada się). W tym przypadku pomocny staje się test t - Studenta. Kontroli istotności kolejno wszystkich parametrów dokonujemy w sposób następujący: a/ stawiamy hipotezy: H0 : bi = 0 ocena parametru nieistotnie różni się od zera. H1 : bi ≠ 0 ocena parametru istotnie różni się od zera. bi - wartość oceny parametru strukturalnego b/ weryfikujemy hipotezy. Dla każdego parametru wyznaczana jest statystyka empiryczna: te = i = 1, 2, ..., k. S(bi) - błąd średni oceny parametru strukturalnego D­­^2 (b) = S^2 (X^TX)^-1 V (bi) - wariancja oceny parametru strukturalnego (odczytana z macierzy wariancji i kowariancji) Statystykę teoretyczną odczytuje się z tablic rozkładu t - Studenta, dla zadanego poziomu istotności α i n - (k+1) stopni swobody. Jeżeli: te ≤ tt nie ma podstaw do odrzucenia hipotezy zerowej H0, czyli ocena parametru nieistotnie różni się od zera, te > tt należy odrzucić hipotezę zerową H0, na rzecz hipotezy alternatywnej - ocena parametru istotnie różni się od zera. Gdy zmienna objaśniająca nie wywiera istotnego wpływu na zmienną objaśnianą należy ją wyeliminować z modelu. Mogą wystąpić następujące sytuacje: niektóre oceny parametrów mogą okazać się nieistotne - trzeba zatem wyeliminować te zmienne, dla których oceny parametrów są nieistotne, a następnie wrócić do etapu III i dokonać ponownej estymacji parametrów modelu dla zmienionej macierzy obserwacji na zmiennych objaśniających, wszystkie parametry są istotne - przystępujemy do kolejnego etapu weryfikacji. Jeżeli występuje współliniowość statystyczna może okazać się, że wszystkie parametry strukturalne modelu są nieistotne. Badanie stacjonarności odchyleń losowych (heteroskedastyczności) Cel: sprawdzenie czy spełnione zostało jedno z założeń KMNK mówiące o stałości wariancji odchyleń losowych. Jeżeli moduły reszt są skorelowane z czasem to rozkład odchyleń losowych nie jest stacjonarny (nie jest homoskedatyczny). Badanie stacjonarności przeprowadzamy analizując istotność współczynnika korelacji modułów reszt z czasem Badanie to przeprowadza się dla modeli zbudowanych w oparciu o szeregi czasowe . Jeżeli rozkład odchyleń losowych nie jest stacjonarny wracamy do etapu III. Należy dokonać ponownej estymacji parametrów modelu uogólnioną metodą najmniejszych kwadratów. Etapy: 1. Stawiamy hipotezy: - H0 : = 0 współczynnik korelacji modułów reszt z czasem nieistotnie różni się od zera; można przyjąć, że rozkład odchyleń losowych jest stacjonarny (homoskedastyczny). - H1 : ≠ 0 współczynnik korelacji modułów reszt z czasem istotnie różni się od zera; rozkład odchyleń losowych nie jest stacjonarny (jest heteroskedastyczny). 2. Obliczamy współczynnik korelacji modułów reszt z czasem według wzoru: - średnia arytmetyczna z modułów reszt (nie moduł ze średniej arytmetycznej). 3. Obliczamy statystykę empiryczną te . 4. Z tablic do testu t - Studenta odczytujemy wartość statystyki teoretycznej tt dla zadanego poziomu istotności α i n- 2 stopni swobody. Jeżeli: te ≤ tt - nie ma podstaw do odrzucenia hipotezy zerowej, współczynnik korelacji modułów reszt z czasem nieistotnie różni się od zera (wariancja odchyleń losowych jest stała); te > tt - odrzucamy hipotezę zerową na rzecz hipotezy alternatywnej, współczynnik korelacji modułów reszt z czasem istotnie różni się od zera (wariancja odchyleń losowych zmienia się w czasie). Badanie autokorelacji odchyleń losowych Cel: sprawdzenie, czy zostało spełnione założenie KMNK, które brzmi: autokorelacja odchyleń losowych nie występuje (ciąg reszt jest ciągiem niezależnych zmiennych losowych). - Autokorelacja oznacza liniową zależność odchyleń losowych pochodzących z różnych okresów badania. - Badanie przeprowadzamy dla modeli zbudowanych w oparciu o czasowe szeregi danych. - Jeżeli autokorelacja występuje, oznacza to, że nie zostało spełnione jedno z założeń KMNK. Należy wrócić do etapu III i dokonać ponownej estymacji parametrów metodą różniczki zupełnej. Przyczyny autokorelacji: 1.Właściwości pewnych zjawisk ekonomicznych. Inercja powiązań między zjawiskami ekonomicznymi i przedłużone w czasie oddziaływanie pewnych zdarzeń na zmienną objaśnianą. 2. Błędy w sztuce ekonometrycznej: - niewłaściwie dobrana postać analityczna modelu, - nieuwzględnienie w modelu wszystkich czynników istotnie oddziałujących na zmienną objaśnianą, - błędne ustalenie opóźnień czasowych dla zmiennych objaśniających. W większości przypadków, jeżeli autokorelacja zachodzi, to jest to właśnie autokorelacja pierwszego rzędu. Zdarzają się jednak sytuacje, gdy zachodzi autokorelacja wyższych rzędów, mimo że nie zachodzi autokorelacja pierwszego rzędu. Badając autokorelację można korzystać z testu Durbina - Watsona lub t - Studenta. Test Durbina - Watsona służy do badania autokorelacji pierwszego rzędu. Aby poprawnie stosować ten test rozpatrywany model musi mieć wyraz wolny, składnik losowy powinien mieć rozkład normalny i w modelu nie może występować opóźniona zmienna objaśniana jako zmienna objaśniająca, ponadto liczba obserwacji musi być co najmniej równa 15. Etapy: 1. Stawiamy hipotezy H0 : ret, et-τ = 0 Współczynnik korelacji reszt dotyczących okresu t (bieżącego) z resztami okresu poprzedniego t - τ (opóźnionego o τ, gdzie τ = 1,2,..,n) nieistotnie różni się od zera. Autokorelacja nie występuje. H1 : ret, et-τ ≠ 0 Współczynnik korelacji reszt dotyczących okresu t (bieżącego) z resztami okresu poprzedniego t - τ (opóźnionego o τ, gdzie τ = 1,2,..,n) istotnie różni się od zera. Występuje autokorelacja. 2. Obliczamy współczynnik korelacji reszt z okresu t z resztami opóźnionymi o τ (współczynnik autokorelacji) według wzoru: gdzie: et - reszty z okresu bieżącego, et - τ - reszty opóźnione o τ okresów. 3. Obliczamy statystykę empiryczną d. Jeżeli: a/ > 0 (autokorelacja dodatnia), to z tablic do testu Durbina - Watsona dla przyjętego poziomu istotności α, n obserwacji oraz k zmiennych objaśniających należy odczytać dwie statystyki teoretyczne dl, du. W przypadku gdy: - d > du - nie ma podstaw do odrzucenia hipotezy zerowej, współczynnik autokorelacji jest nieistotny, autokorelacja nie występuje, - d < dl - to hipotezę zerową należy odrzucić na rzecz hipotezy alternatywnej, współczynnik autokorelacji jest istotnie różny od zera, występuje autokorelacja, - dl d du - to przy użyciu testu Durbina - Watsona nie można podjąć żadnej decyzji. Należy zastosować inny test b/ < 0 (autokorelacja ujemna ),należy obliczyć wartość statystyki d`: d` = 4 - d Z tablic do testu Durbina - Watsona dla przyjętego poziomu istotności α, n obserwacji oraz k zmiennych objaśniających należy odczytać dwie statystyki teoretyczne dl, du. W przypadku gdy: - d` > du - nie ma podstaw do odrzucenia hipotezy zerowej, współczynnik autokorelacji jest nieistotny, autokorelacja nie występuje - d` < dl - to hipotezę zerową należy odrzucić na rzecz hipotezy alternatywnej, współczynnik autokorelacji jest istotnie różny od zera, występuje autokorelacja. - dl d` du - to przy użyciu testu Durbina - Watsona nie można podjąć żadnej decyzji. Należy zastosować inny test Badanie autokorelacji testem t - Studenta (służy do badania autokorelacji pierwszego i wyższych rzędów) Etapy: 1. Stawiamy hipotezy H0 : ret, et-τ = 0 Współczynnik korelacji reszt dotyczących okresu t (bieżącego) z resztami okresu poprzedniego t - τ (opóźnionego o τ, gdzie τ = 1,2,..,n) nieistotnie różni się od zera. Autokorelacja nie występuje. H1 : ret, et-τ ≠ 0 Współczynnik korelacji reszt dotyczących okresu t (bieżącego) z resztami okresu poprzedniego t - τ (opóźnionego o τ, gdzie τ = 1,2,..,n) istotnie różni się od zera. Występuje autokorelacja. 2. Obliczamy współczynnik korelacji reszt z okresu t z resztami opóźnionymi o τ (współczynnik autokorelacji) według wzoru: gdzie: et - reszty z okresu bieżącego, et - τ - reszty opóźnione o τ okresów. 3. Obliczamy statystykę empiryczną te . 4. Z tablic do testu t - Studenta odczytujemy wartość statystyki teoretycznej tt dla zadanego poziomu istotności α i n - 2 - τ stopni swobody. Jeżeli: te ≤ tt - nie ma podstaw do odrzucenia hipotezy zerowej, współczynnik autokorelacji nieistotnie różni się od zera - autokorelacja nie występuje; te > tt - odrzucamy hipotezę zerową na rzecz hipotezy alternatywnej, współczynnik autokorelacji istotnie różni się od zera - autokorelacja występuje;

WERYFIKACJA MODELU Czwarty etap procedury badań ekonometrycznych to weryfikacja modelu. Celem tego etapu jest sprawdzenie poprawności modelu i ewentualna korekta jego niedociągnięć (doprowadzenie modelu do zastosowania w poprawnej formie). W ramach weryfikacji sprawdzamy: a/ stopień przylegania modelu do opisywanego przezeń fragmentu rzeczywistości ekonomicznej (dopasowanie modelu do danych empirycznych), b/ wpływ zmiennych objaśniających na zmienną objaśnianą, poprzez ocenę istotności parametrów strukturalnych modelu, c/ rozkład elementu losowego (rozkład reszt) w celu zweryfikowania słuszności założeń leżących u podstaw wyboru metody estymacji. Kroki weryfikacji: badanie koincydencji, badanie dopuszczalności, badanie normalności rozkładu elementu losowego, badanie symetrii rozkładu elementu losowego, badanie losowości rozkładu elementu losowego, badanie istotności parametrów strukturalnych, badanie nieobciążoności rozkładu elementu losowego, badanie stacjonarności elementu losowego (heteroskedastyczności), badanie autokorelacji elementu losowego. KROK I: badanie koincydencji Cel: sprawdzenie sensowności ocen parametrów strukturalnych ze względu na znak. Brak koincydencji może wynikać z występowania współliniowości statystycznej zmiennych, ponieważ współliniowość może powodować, że znaki współczynników regresji będą odmienne od oczekiwanych. Sprawdzamy czy znak oceny stojącej przy j-tej zmiennej objaśniającej jest zgodny ze znakiem współczynnika korelacji j- tej zmiennej objaśniającej ze zmienną objaśnianą, tj.: sgn bj = sgn ro­j Jeżeli własność ta zachodzi, to oznacza, że ocena bj jest sensowna ze względu na znak. Jeżeli wszystkie oceny parametrów stojące przy zmiennych objaśniających są sensowne ze względu na znak, to model posiada własność koincydencji. Aby sprawdzić koincydencję modelu należy obliczyć wektor współczynników korelacji zmiennych objaśniających ze zmienną objaśnianą Ro (por. np. ćw. 1) : r02 = 0,57182 r04 = 0,69231 a zatem sgn r02 = ”+” i sgn b2 = “+”, co oznacza, że znak współczynnika korelacji drugiej zmiennej objaśniającej jest taki sam jak znak oceny stojącej przy drugiej zmiennej objaśniającej. Analogiczna sytuacja występuje w przypadku czwartej zmiennej objaśniającej: sgn r04 = “+” oraz sgn b4 = “+”. Model spełnia warunek koincydencji, co pozwala przejść do kolejnego kroku weryfikacji. KROK II: badanie dopuszczalności modelu Cel: sprawdzenie w jakim stopniu oszacowany model wyjaśnia kształtowanie się zmiennej objaśnianej oraz sprawdzenie poprawności doboru postaci analitycznej. Dopuszczalność modelu bada się dla wszystkich modeli z tym, że: dla modeli nieliniowych sprowadzalnych do liniowych dla postaci pierwotnej modelu, dla modeli segmentowych, dla całego zbioru segmentów łącznie. = + - wariancja zmiennej objaśnianej - część wariancji zmiennej objaśnianej wytłumaczona przez zmienne objaśniające modelu S^2 - wariancja resztowa jest częścią wariancji zmiennej objaśnianej, która zależy od czynników losowych, a więc nie jest wyjaśniana przez zmienne objaśniające modelu. Jeżeli okaże się, że model nie jest dopuszczalny należy wrócić do 1 lub 2 etapu badań ekonometrycznych (decyzję w zależności od przyczyny braku dopuszczalności podejmuje prowadzący badania). Do miar dopasowania modelu do danych empirycznych zalicza się: współczynnik zbieżności, współczynnik determinacji i skorygowany współczynnik determinacji. Współczynnik zbieżności W celu sprawdzenia stopnia dopasowania modelu do danych rzeczywistych należy obliczyć współczynnik zbieżności wg wzoru: Współczynnik zbieżności informuje: o udziale wariancji resztowej w ogólnej wariancji zmiennej objaśnianej, jaka część zmienności zmiennej objaśnianej nie została wyjaśniona przez zmienne objaśniające modelu czyli kształtuje się w sposób losowy. Współczynnik zbieżności przyjmuje wartości z przedziału <0,1>. ϕ^2 = 0 oznacza, że kształtowanie się zmiennej objaśnianej jest w pełni wyjaśnione przez zmienne objaśniające modelu - w modelu takim nie uwzględnia się elementu losowego, jest to model deterministyczny, ϕ^2 = 1 zmienne objaśniające uwzględnione w modelu nie wyjaśniają kształtowania się zmiennej objaśnianej, ϕ^2 = 0,2 informuje o tym, że 20% zmienności zmiennej objaśnianej nie zostało wyjaśnione przez zmienne objaśniające modelu. Aby sprawdzić, czy model jest dopuszczalny należy: określić wartość krytyczną współczynnika zbieżności - przyjmuje się, że wartość krytyczna współczynnika zbieżności nie powinna przekroczyć 0,3 (co oznacza, że 30% zmienności zmiennej objaśnianej kształtuje się w sposób losowy), obliczyć wartość empiryczną współczynnika zbieżności , porównać te wartości: jeżeli ≤ model jest dopuszczalny, gdy > model nie jest dopuszczalny. Współczynnik determinacji Współczynnik determinacji informuje: o udziale wariancji zmiennej objaśnianej wyjaśnianej przez zmienne objaśniające modelu w ogólnej wariancji zmiennej objaśnianej, jaka część zmienności zmiennej objaśnianej została wyjaśniona przez zmienne objaśniające modelu (kształtuje się pod wpływem czynników uwzględnionych w modelu). Współczynnik determinacji R^2∈<0,1>. R^2 = 0 zmienne objaśniające uwzględnione w modelu nie wyjaśniają w żadnym stopniu kształtowania się zmiennej objaśnianej R^2 = 1 oznacza to, że zmienna objaśniana jest w pełni wyjaśniona przez zmienne objaśniające modelu - w modelu takim nie uwzględnia się elementu losowego, jest to model deterministyczny, R^2 = 0,78 informuje o tym, że 78% zmienności zmiennej objaśnianej zostało wyjaśnione przez zmienne objaśniające modelu. Pomiędzy współczynnikiem zbieżności a współczynnikiem determinacji występuje następująca zależność: R^2 + ϕ^2= 1, czyli R^2 = 1- ϕ^2 Wartość R^2 : powyżej 0,9 należy uważać za bardzo dobrą, powyżej 0,8 za dobrą, a powyżej 0,6 za zadowalającą w niektórych zastosowaniach, choć należy się wówczas liczyć z dużymi błędami prognozy, poniżej 0,5 - model wyjaśnia tylko mniej niż 50% zmienności zmiennej objaśnianej, prognozy mogą okazać się nietrafne, niższe wartości współczynnika są do przyjęcia, jeżeli chcemy jedynie zrozumieć związki między zmiennymi. Pierwiastek kwadratowy ze współczynnika determinacji to współczynnik korelacji wielorakiej (R) (wróć pamięcią do lab. 1). Wadą zarówno współczynnika zbieżności, jak i współczynnika determinacji jest to, że ich wartości zależą od liczby zmiennych objaśniających modelu, co utrudnia porównywanie jakości modeli o różnej liczbie zmiennych objaśniających. Mianownik we wzorze na współczynnik zbieżności zależy wyłącznie od wartości empirycznych zmiennej objaśnianej, natomiast licznik jest funkcją zarówno zmiennej objaśnianej jak i zmiennych objaśniających. Zwiększenie liczby zmiennych objaśniających zmniejsza (lub przynajmniej nie zwiększa) wartości reszt, dlatego powoduje zazwyczaj wzrost współczynnika determinacji. Jednak może to być jedynie pozorna poprawa dopasowania model do danych empirycznych wynikająca ze zmniejszenia liczby stopni swobody (n - (k+1)). Ten sam skutek (pozorny wzrost dopasowania modelu) uzyskamy zmniejszając liczbę stopni swobody poprzez zmniejszanie liczby obserwacji (n). Dlatego coraz częściej stosuje się wolny od tej wady skorygowany współczynnik determinacji . Współczynnik ten stosowany jest często do porównywania jakości różnych modeli zbudowanych w oparciu o różną liczbę zmiennych objaśniających lub różną liczbę obserwacji. Może być stosowany także, gdy należy zdecydować, czy warto do modelu wprowadzić dodatkową zmienną objaśniającą. Decyzję o dodaniu dodatkowej zmiennej możemy podjąć wtedy, gdy wywoła to wzrost skorygowanego współczynnika determinacji. : Badanie normalności rozkładu elementu losowego Cel: sprawdzenie zgodności rozkładu elementu losowego z rozkładem normalnym, czyli jednego z założeń KMNK. Jeżeli element losowy ma rozkład normalny, to estymator uzyskany za pomocą KMNK ma własności użyteczne w konstruowaniu testów statystycznych w celu sprawdzania różnych cech modelu ekonometrycznego. Pozytywna ocena normalności rozkładu elementu losowego ma zasadnicze znaczenie dla procesu weryfikacji modelu (umożliwia stosowanie testu t - Studenta i F Fishera - Snedecora). Ponadto, jeśli model ma służyć celom prognostycznym, to w przypadku gdy element losowy ma rozkład zbliżony do normalnego przy obliczaniu prognozy otrzymamy węższy przedział prognozy, a tym samym większą precyzję prognozy. Prognoza obarczona jest również mniejszym błędem. Etapy badania normalności rozkładu elementu losowego: 1. Stawiamy hipotezy: H0 : F(et) ≅ F(N) Dystrybuanta reszt jest zbliżona do dystrybuanty rozkładu normalnego. H1 : F(et) ≅ F(N) Dystrybuanta reszt w sposób istotny odbiega od dystrybuanty rozkładu normalnego. 2. Porządkujemy reszty rosnąco. 3. Dokonujemy standaryzacji reszt według wzoru (korzystając z odchylenia standardowego reszt - S): e't = - w modelach liniowych szacowanych KMNK suma reszt równa jest zero, co oznacza że średnia arytmetyczna reszt również jest równa zero. 4. Dla każdej reszty standaryzowanej odczytujemy z tablic dystrybuanty rozkładu normalnego wartości dystrybuant F( ). 5. Tworzymy „CELE” - przedział liczbowy <0,1> dzielimy na n równych podprzedziałów It. Należy ustalić ke - oznaczające liczbę pustych cel, czyli przedziałów, do których nie trafiła żadna wartość odczytana z tablic dystrybuanty rozkładu normalnego. Dla modeli zbudowanych na co najwyżej 30 obserwacjach (mała próba) należy odczytać z tablicy do testu zgodności Hellwiga wartości teoretyczne k1 i k2 dla określonej liczby obserwacji n i zadanego poziomu istotności α. W przypadku gdy: k1 ≤ ke ≤ k2 - nie ma podstaw do odrzucenia H0. Można przyjąć, że rozkład reszt jest zbliżony do rozkładu normalnego, k1 > ke > k2 - odrzucamy H0 na rzecz H1. Nie można przyjąć, że rozkład reszt jest zbliżony do rozkładu normalnego.

---