KAROLINA KRÓLAK GR.2
ZADANIA II - ROZWIĄZANIA
ZADANIE 1. Dla równoważnych stóp ![]()
i ![]()
wyprowadzić formułę ![]()
.
ROZWIĄZANIE:
dla ![]()
mamy: 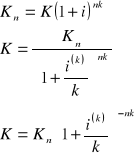
dla ![]()
mamy: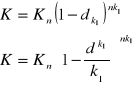
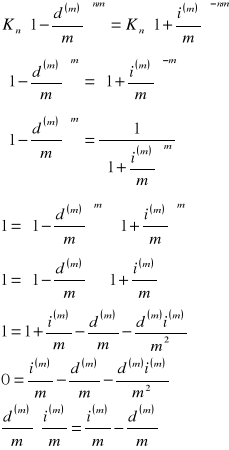
co było do pokazania.
ZADANIE 2. Korzystając z poprzedniego zadania pokazać, że ![]()
.
ROZWIĄZANIE:
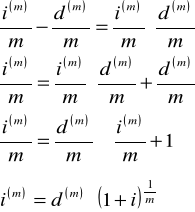
ZADANIE 3. Znając ![]()
oraz ![]()
wyznaczyć ![]()
.
ROZWIĄZANIE:

ZADANIE 4. Nominalna stopa oprocentowania ciągłego jest funkcją czasu ![]()
,![]()
. Znaleźć średnią stopę oprocentowania ciągłego i równoważną efektywną roczną stopę oprocentowania składanego ![]()
w tym okresie.
Wskazówka: ![]()
, ![]()
.
ROZWIĄZANIE:
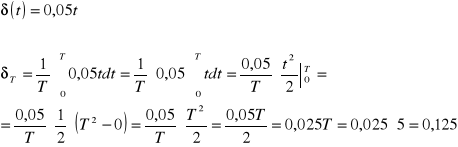
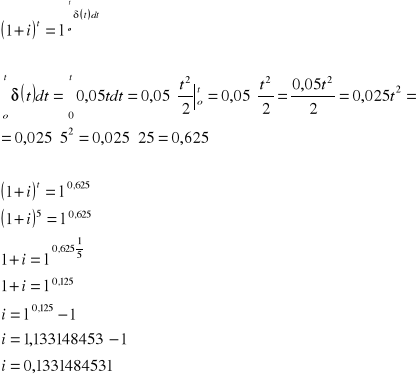
ZADANIE 5. Znaleźć zakumulowaną wartość $1 na koniec 15 lat, jeżeli ![]()
.
Wskazówka: ![]()
.
ROZWIĄZANIE:
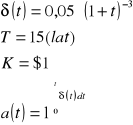
![]()
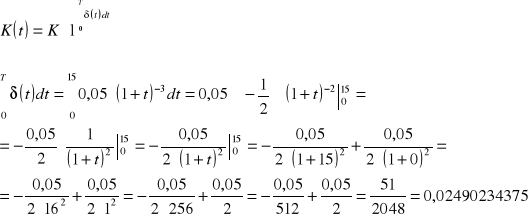
więc 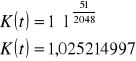
ZADANIE 6. Znaleźć efektywną roczną stopę oprocentowania składanego ![]()
obowiązującą w okresie trzech lat równoważną zmiennej stopie dyskonta w tym okresie: ![]()
w pierwszym roku ![]()
w drugim roku i ![]()
w trzecim roku.
Wskazówka: ![]()
.
ROZWIĄZANIE:
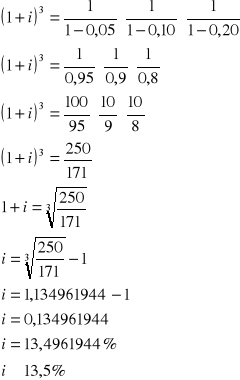
ZADANIE 7. Nominalna stopa oprocentowania ciągłego wyraża się wzorem ![]()
![]()
dla ![]()
. Dla dowolnego okresu rocznego pomiędzy rokiem ![]()
i ![]()
wyznaczyć równoważną nominalną stopę dyskontową ![]()
.
Wskazówka: Wyznaczyć najpierw ![]()
, następnie stopę dyskontową w okresie rocznym pomiędzy ![]()
i ![]()
(z zależności ![]()
)
i w końcu szukane ![]()
dla tego okresu.
ROZWIĄZANIE:
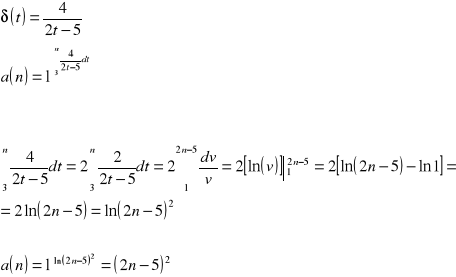
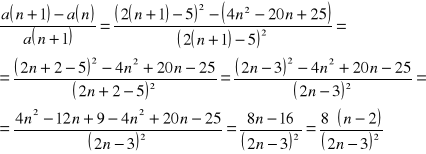
podstawiam n=4 i otrzymuję: ![]()
Korzystając ze wzoru 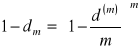
wyliczam szukane ![]()
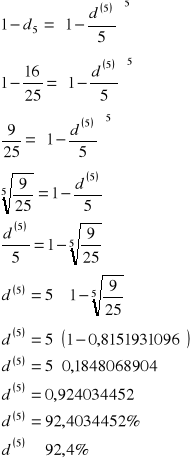
ZADANIE 8. Korzystając z poznanych zależności: 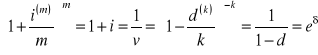
obliczyć następujące pochodne:
a) ![]()
, b) ![]()
, c) ![]()
, d) ![]()
, e) ![]()
.
ROZWIĄZANIE:
a)
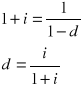
![]()
b)
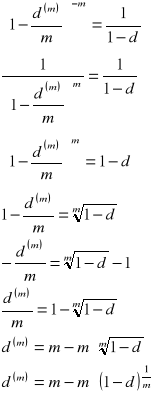
![]()
c)
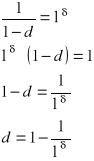
![]()
d)
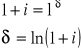
![]()
e)
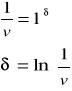
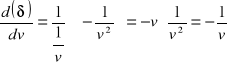
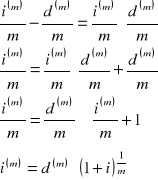
Wyszukiwarka
Podobne podstrony:
ściąga organizacja, Politologia WSNHiD, Licencjat, III SEMESTR, Organizacja i zarządzanie
wykład - cz. II (1), AKADEMIA MORSKA - MAteriały II ROK . TRANSPORT I LOGISTYKA, cały syf z III SEME
Pytania na Wspolczesna Systemy Polityczne, Politologia WSNHiD, Licencjat, III SEMESTR, Współczesne s
elektro Cw1, AKADEMIA MORSKA - MAteriały II ROK . TRANSPORT I LOGISTYKA, cały syf z III SEMESTRU, je
ściąga - komunikacja, Politologia WSNHiD, Licencjat, III SEMESTR, Komunikacja
Ćwiczenie nr 1 radek i kamil, AKADEMIA MORSKA - MAteriały II ROK . TRANSPORT I LOGISTYKA, cały syf z
ZEW II, ZEW i EP Kolegium Nauczycielskie w Bytomiu, III semestr
CI GA Z NUMERK W, Budownictwo Politechnika Warszawska, Semestr III, III Semestr, Przodki 3 sem, nume
IKII OS, Budownictwo Politechnika Warszawska, Semestr III, III Semestr, Przodki 3 sem, Przodki, Inży
odpowiedzi na pytania, Budownictwo Politechnika Warszawska, Semestr III, III Semestr, Przodki 3 sem,
Notatka II FiR, Studia UMK FiR, Licencjat, II rok - moduł Rachunkowość, Finanse publiczne R.Huterski
Notatka II FiR, Studia UMK FiR, Licencjat, II rok - moduł Rachunkowość, Finanse publiczne R.Huterski
Prawo finansowe W I, administracja, II ROK, III Semestr, rok II, sem IV, prawo
prawo finansowe 17.03.05, administracja, II ROK, III Semestr, rok II, sem IV, prawo finansowe
Ekonomia matematyczna egz 30.01.2015, Ekonomia II stopień, UMK 2013-2015, III semestr, Ekonomia mate
prawo finansowe W 11.04.05, administracja, II ROK, III Semestr, rok II, sem IV, prawo finansowe
Quiz 2 (II wersja), Studia, III semestr, Finanse publiczne
więcej podobnych podstron