Wykład I
Duże zadania dzieli się na podzadania. Zadania wykonywane są na pewnych jednostkach. Cel to: przyspieszenie realizacji.
Procesor: jednostka sterująca+ jednostka logiczno-arytmetyczna.
Realizacja systemów równoległych:
komputer równoległy- łączy procesory
sieć stacji roboczych (system rozproszony lub klaster) - połączenie komputerów
PRZETWARZANIE ROZPROSZONE:
Ma miejsce w sieciach stacji roboczych ( sieciach lub systemów rozproszonych)
Sieci komputerowe:
LAN- protokoły Ethernet, fast Ethernet
MAN- protokoły ATM- zapewnia skalowalność, przepustowość 2 Mb/s
WAN- protokoły ATM o większej przepustowości , można przekazywać nawet rozmowy telefoniczne.
PRZETWARZANIE RÓWNOLEGŁE: (używane w systemie klient- serwer)
w LAN
w WAN (metoda komputer)
serwer www
serwer FTP (dostarczają pliki)
serwery pocztowe
serwer IRC
serwery baz danych
PRZETWARZANIE WSPÓŁBIEŻNE:
dotyczy wielu niezależnych zadań
umożliwia obsługę wielu zadań i minimalizację śred. czasu reakcji systemu na żądanie obsługi zadania użytkownika.
System równoległy:
przetwarzanie równoległe
przetwarzanie współbieżne (serwer)
system rozproszony:
przetwarzanie równoległe
przetwarzanie typu klient- serwer
Wykład I
Średni czas reakcji: tRśredni= (10+20+30)/3= 20
Furiera równanie: (przewodzenie ciepła) 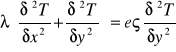
λ-współczynnik przewodnictwa
ς- gęstość
e- ciepło
metoda stosowana do skomplikowanych geometrii. Dzieli się obiekt na elementy skończone, potem dyskretyzacja względem przestrzeni i w czasie (całkowanie względem czasu i po czasie)
eςMTn+1 ≠λΔtkTn+1=eςMTn+1+ bn+1
układ rozwiązujemy dla kolejnych kroków czasowych
temperatura w kroku następnym :A- macierz dana ATn+1=bn
b- uwzględnia warunki brzegowe
szerokość półpasma W=2b-1
dzieli się siatkę na podsiatki i przyporządkowujemy pdsiatki procesorom. Podsiatki mają połączenia.
9,12,7- w tych węzłach obl. jest temperatura danych procesorów.
Minimalizacja operacji komunikacyjnej pomiędzy poszczególnymi procesorami.
Każdy procesor powinien mieć tyle samo pracy do wykonania.
Zadania optymalizacji zadania NP.- trudnego:
minimum różnicy obciążeń procesorów
min. liczba przesyłanych danych
nie ma idealnych algorytmów do rozwiązań o złożoności polinionalnych
Elementy równoległościowe są w procesorach skowych.
zmniejszona l .rozkazów
uproszczenie struktury procesora.
Wykład II
ZASADA POTOKOWOŚCI
Super skalarna architektura RISC
Przetwarzanie potokowe - jak wykonać poszczególne instrukcje w komputerze:
1. wczytanie rozkazu
2. dekodowanie rozkazu
3. wczytanie danych
4. wykonanie operacji
5. zapisanie wyników do pamięci
6. wyznaczyć adres następnego rozkazu
Do każdego etapu mamy osobne urządzenia:
2) c=a-b
3) if c >0 then d = √c else d=a+b
Architektura równoległa - klastracja
1.Flynn'a - liczba punktów instrukcj
- liczba potoków danych
1. SISD single
2. MISD multiple
3. SIMD insert
4. MIMD data
Realizacja MIMD - możemy podzielić na :
-distributed memory (rozproszona)
Multiprocesor:
1.programowanie jest bardziej zbliżone do oprogramowania komputerów sekwencyjnych, bo dane są zmiennymi globalnymi, wspólne dla procesorów, dostęp do pamięci jest wąski (do 16) dlatego jest gorsz skalowalność
Multikomputer:
2. Zmienne są lokalne, duża dobra skalowalność, liczbę procesorów można
Zwiększyć tak jak wydajność. komunikację trzeba programować
SMP - symetryczny multiprocesor, żaden procesor nie jest wyróżniony, ma dostęp do jądra
VSM virtual SM
DSM distributed Sm
NUMA - system z niejednorodnym dostępem do sieci
CCNUMA- z zapewnieniem kocherentości
Najbardziej efektywne są systemy z pamięcią rozproszoną.
Architektury możemy podzielić na rodzaj sieci komp:
1.DYNAMICZNE - składające sie z przełączników
2.STATYSTYCZNE - połączenia typu punkt do punktu
1. Dynamiczne: magistrala
w danym momenci tylko jedna para może się komunikować.
połączenia krzyżowe : przełącznik mamy N2 - są stosowane w centralach telefonicznych
Nie ma konfliktów, każdy procesor może się kontaktować z blokiem pamięci, jeśli jednocześnie z tym samym, to musi być on wieloportowy.
SIECI WIELOSTOPNIOWE MULTI_STAGE_ NET WORKS
Omega
Jak się odbywa przesyłanie danych do bloków pamięci RUTING:
1.z komutacją pakietów
2. z przełanczaniem obwodów
1. Pakiet sam toruje drogę. Przy przesyłaniu możliwe są konflikty.
Switch- odp. koncepcji sieci wielostopniowych (Eth- switch lokalizuje ruch w danym segmencie- izoluje)
Budowane są jako sieci wielostopniowe. Switch w sieciach lokalnych służy do izolacji sieci, lokalizuje ruch sieci (Ethernet) w poszczególnych segmentach. Może jednocześnie uzyskiwać połączenie kilku komputerów między sobą. Do każdego wejścia switcha można podłączyć jeden komputer. Sieci MAN składają się z kilku switchy:
Jest budowany na zasadzie Crossbar lub jako sieć wielostopniowa. Przełączniki ATM
Może być struktura drzewiasta. HOPS - skoki ; polecenie pozwala nam zobaczyć wszystkie skoki.
SIECI STATYCZNE- składają się z połączenia punkt do punktu, stosuje się w systemach z pamięcią rozproszoną.
KOSZT- ogólna liczba połączeń; Lp - liczba portów w węźle P;
WYDAJNOŚĆ - średnica sieci - d- max odległość pomiędzy dwoma wierzchołkami;
- szerokość bisekcji B
Lp = N-1 Lp = (∑Pi)/2
P=2 - ilość max wyjść
D= N-1
B- min liczba krawędzi grafu, które trzeba
usunąć aby podzielić graf na dwie równe części. Im średnica większa tym wydajność mniejsza. P=2 Lp=N d=N/2 B=2
RING
D=N/2
P=2
Lp=N
B=2
2Dmesh - siatka dwuwymiarowa
P=4
d= 2b-2 b=√ N -1 d=2 √N -2 Lp=2N-2N=2N
b=√N
Aby poprawić sieć trzeba zastosować torus:
P=4 Lp= 2N B=2√N d=√N -1
Sieć ta jest często stosowana. Siatka ma ważną cechę. Struktura połączeń między procesami ma zastosowanie w algorytmach.
Możemy wstawić switcha to mamy sieć dynamiczną (w miejsce C). Do sieci statycznej możemy zaliczyć drzewo. Wierzchołki to procesory. Struktura drzewiasta odpowiada algorytmom hierarchicznym.
HYPER - CUBE = HIPER SZEŚCIAN (gdy mamy dużo procesorów)
!!!!!
d=r=log2N P=r=log2N B=N/2 Lp=N*P/2
RUTING w sieci: przesyłanie komunikatów z jednego wierzchołka do drugiego.
MAPPING zagadnienie odwzorowania. Mamy przesłać P0 - P1 - P2 - P3 jeden komunikat STORE-AND-FORWARD - zapamiętaj i przekaż dalej.
CZAS PRZESYŁANIA:
t= tSTARTU+l*t + l*m*tB=tS+tm+tB
l - liczba hops
t - t przesyłania nagłówka
m - długość słowa w bajtach
tB - czas przesłania jednego bajtu
CUT-AND-TROUGH
t= ts + m*tB+(l-1) * tm
0 ( m+l )
0 ( m )
t = ts +m tB
Wyklad IV
Algorytm równoległego mnożenia macierzy:Cij=Σaikbkj
Zapis wskaźnikowy: cij=ain*bnj dla i=0,..,M.-1 j=0,..,N-1, K=0,..,K-1
Duże zadania dzielą się na podzadania, które są podzadaniami zależnymi. Graf zorientowany (bo ma strzałki) i acykliczny (każdy wierzchołek jest przechodzony tylko raz). Jedno podzadanie odpowiada obliczeniu jednego elementy macierzy C. Podzadania maja swoje dane, które są przekazywane między podzadaniami.
Efektywność realizacji algorytmu równoległego:
Min czas realizacji algorytmu:
Tmin(M+N-1)*Tp Tp-czas podzadania Tp=2k*Toperacji (2k bo 2 działania w macierzach + i *)
Tp - czas mnożenia wiersza przez kolumnę
Trzeba znaleźć wszystkie ścieżki krytyczne (łączy wierzchołki typu źródło i ujście) i wybrać te o max dł.(najpierw znajdujemy wszystkie drogi ze źródła do ujścia, które sa min, a potem z tych min wybieramy max)
Sortowanie topologiczne grafu: rozdzielenia algorytmu na warstwy z których każda jest zależna od poprzedniej. Ilość warstw da nam min czas rozwiązania algorytmu. Szerokość grafu: jeśli M=N to W=M jest to max ilość procesorów, które mogą być w określonym czasie wykorzystywane.
Czas real algor na P prockach: (M=N=K)->N dla każdego podzadanie wydzielamy swój procesor P=N2 Tp=(2N-1)*2N*Toperacji
Przyspieszenie(speed-up): ile szybciej działa dany algorytm na architekt równoległej w porównaniu ze sposobem sekwencyjnym.
Sp=T1/Tp P=>Sp=>1
T1=N2*2N=2N3
Aby uzyskać el wynikowy mnożymy el w jednej i drugiej macierzy i dodajemy następnie mnożenie. Dla jednego el wykonujemy 2N mnożeń. Ponieważ macierz wynikowa jest N*N to mnożymy jeszcze razy N2 bo tyle jest el.
SN2=1/2N
(T1 - czas algorytmu na 1 procku - ilość operacji, Tp - czas algor na P prockach) Wyróżniamy: superprzyspieszenie (wraz ze wzrostem ilości procków wzrasta ilość cachu[pamięci]), idealne(liniowe zmniejszenie czasu do zwiększenia ilości procków) oraz rzeczywiste.
Efektywność: Ep - efektywność realizacji algorytmu na P prockach, stosunek pracy
uzyskanej do włożonej, stosunek rezultatu do kosztu. Ep=Sp/P (Sp-przyspieszenie, P- ilość procków). 0<Ep<=1.
Graf acykliczny: (zorientowany) bez zapętlenia algorytmu, ujście nie może się połączyć z źródłem(odwrotnie tak).
Prawo Amdall'a : [mamy algorytm gdzie część jest sekwencyjna (β) a część równoległa (1-β)] Tp=β*T1+[(1-β)*T)/P
Sp=T1/[β*T1+([1-β]*T1)/P można wnioskować że architekturę równoległą opłaca się stosować w rozległych algorytmach.
Narzuty na architekturę: różne dodatki
Tparell=Ts+Tov (Tov - overheads narzuty czyli czas narzutu,Ts - czs algorytmu sekwencyjnego)
Tc - komunikacja, TN - nierównoważenie się komputera, TD-dodatkowe operacje.
Wykład V
Ziarnistość-parametr decydujący o efektywności
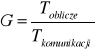
GA≥0 -warunek
To-czas wykonania obliczeń
Tk-czas wykonania bazowej komunikacji operacyjnej definiowana dla komputera lub algorytmu
GA-komputera GA- algorytmu
-gdy ziarnistość komputera GK jest mała to duży narzut na komunikację
-gdy GK duża to mały narzut na komunikację
można def dla komp i dla algorytmów. Ziarnistość komp i algorytmu powinna być porównywalna, aby działanie było efektywne
Ziarnistość algorytmu liczymy:
Liczymy dla c11
![]()
W-dł.słowa
TB-czas potrzebny do przesyłania 1 bit
Czas komutacji TK=ts+βN
ts-czas startu (nieuwzględniany)
βN-odwrotność przepustowości
W przypadku stacji roboczej:
![]()
np.:kom.500MHz-częsytliwość
![]()
wtedy![]()
czas potrzebny do przesyłania 1 B Ethernet 10Mb/s=b
![]()
![]()
![]()
*10-6
Gdy Gkmała bo duże narzuty na komunikację to GA należy zwiększyć
Gdy macierz N na N to procesorów N2
B1 |
B2 |
B3 |
Mamy macierz 100 na 100 i chcemy na 9 procesorach
A1 |
A2 |
A3 |
C00 |
C01 |
|
|
C11 |
|
|
|
C22 |
Mnożenie pasów przez pasy
Rozmiary wierszy i kolumn zaokrąglone w górę[W/P]
Gdy ziarnistość się zwiększa to l. Procesorów zmniejsza się
Gdy chcemy żeby ziarnistość = l.procesorów to macierz musi być większa
Np.:dla dwuwymiarowej macierzy
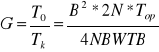
To=B*B*N*Top
Tk=4*N*B*W*TB
B=N/P wielkość bloku
Im blok jest większy tym ziarnistość wzrasta B razy (B-zysk)pole ziarenka jest proporcjonalne do r2czyli T0/Tk=r2/r=r
Rodzaje algorytmów mnożenia macierzy
1)
T=czas=(3N-2)2N*top
Czas realizacji: T=N*2N*Top
2) każdy element utworzy się 1 raz
T=N*2N*Top
Wykład IV
![]()
![]()
procesor na chipe - czas kom do czas obl jest niski ze wzg na kom; można stosować grubo i drobnoziarniste. Używanie grubo nie ma sensu bo będzie za mało ziaren i nie wykorzystamy wszystkich procesorów
komp+sieć komp - narzuty na kom duże, czyli kom droga - nadają się gruboziarniste algorytmy
gdy kom jest szybka można stosować algorytmy drobnoziarniste. Gruboziarniste, które wykorzystują mało kom stosujemy, gdy kom jest droga
METODOLOGIA KONSTRUOWANIA ALGORYTMÓW RÓWNOLOGŁYCH
1.Wydzielenie podzadań w algorytmie (szeregowym). 2.Określenie zależności między podzadaniami. 3. Agregacja podzadań. 4.Wyznaczenie przydziału podzadań do procesorów znana staje się topologia komunikacji między procesorami. 5.Wyznaczenia momentów wykonania poszczególnych podzadań.
-czas realizacji algorytmów,
-przyspieszenie, -efektywność,
-uszeregowanie w czasie podzadań.
Takt musi być większy od czasu operacji
T > max TO
ALGORYTM FILTR CYFROWY(splot liniowy)
![]()
ciągi wejściowe:
W(k) - k=0,...,k-1 charakterystyka filtra
x(i) - i=0,...,N-1 ciąg wejściowy
y(j) - j-0,...,N+k-1
Charakterystyka dla filtra low-band
k=4
N=1024x1024
y(0)=W(0)*x(0)
y(1)=W(0)*x(1)+W(1)*x(0)
y(2)=W(0)*x(2)+x(1)*W(1)+W(2)*x(0)
y(3)=W(0)*x(3)+W(1)*x(2)+W(2)*x(1)+W(3)*x(0)
y(4)=W(0)*x(4)+W(1)*x(3)+W(2)*x(2)+W(3)*x(1)
y=y+w*x
Projekcje wykonujemy wzdłuż osi j, bo będzie najmniej procesorów
x- musi być przekazywany dwa razy wolniej niż y przy realizacji synchronicznej
1.Czas misi biec do przodu.
2.Żadne dwa podzadania nie mogą być wykonywane w żądanym procesorze jednocześnie.
Czas realizacji operacji:
N=7
k=4
T=(N)+(k-1)+(k-1)
T=N+2K-2
Wykład -
Wieloprocesorowe komp klasy PC - architektura SMP (symetryczny multiprocesor: bus-based), każdy procesor ma taki sam dostęp do pamięci
Rys.
Cache-cohorency - zapewnienie spójności cache'u
Występuje wąskie gardło - trudno jest zwiększyc liczbę procesorów
SMP wspierają: UNIX, Win NT, W2K
Athlon (k7) - zamiast magistrali jest sieć komunikacyjna, pozwala na większą liczbę połączeń
CCNUMA
Rys.
Tendencje:
rozwój klastrów stacji roboczych
rozwój wieloprocesorów komp klasy PC o architekturze: SMP, dancechau, CCNUMA
Przekształcenie F - jest to macierz, bo jest to odwzorowanie liniowe
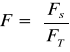
Graf G=<V,E>→C=<S,T,Φ>
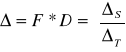
Mnożenie macierzy:
For(i=0; i<M; i++)
For(j=0; j<N; j++)
{ Cij=0;
For(k=0; k<K; k++)
Cij+=aik*bkj; }
n=3
K3={K=(i,j,k): 0≤i≤M-1;0≤j≤N-1; 0≤k≤K-1;}
K3⊂Z3
0 0 1 i
D= 0 1 0 j
1 0 0 k
f00 f01 f02
F= f10 f11 f12 m+1≤n
f20 f21 f22 n=3
m.=2,1
Projekcja wzdłuż osi i
i j k
Fs= 0 0 1 detF≠0
0 1 0
Żadna kolumna nie może być=0
FT*da ≥1 → f21≥
FT*db ≥1 → f20≥
FT*dc ≥1 → f22≥
da
FT ( f20 f21 f22 ) 0 FT=[1,1,1]
1
0
0 0 1
F= 0 1 0
1 1 1 detF= -1
S T
KS2 ΔS KT1 ΔT
K S2 - procesory
ΔS - połączenia pomiędzy nimi
KT1 - momenty pracy procesorów
ΔT - z jaką częst. Poszczególne zmienne są przekazywane między procesorami
K S2={ K S=(k, j); 0≤k≤K-1; 0≤j≤N-1 }
ΔS=F*D=1 0 0
0 1 0
δc δa δb
KT1={ KT=(t); 0≤t≤(N-1)+(M.-1)+(K-1) }
min≤t≤max
T=max-min+1 = N+M+K-2
ΔT=FT*D=[1,1,1]
Algorytm eliminacji Gaussa LU
A=LU /*L-1
L-1*A=U
MA=U A=[A*/b]
b - wektor prawych stron
A - macierz, składa się z macierzy wejściowej rozszerzonej o 1
Algorytm:
for(k=0; k<N-2; k++)
for(i=k+1; i<N; i++) ( k- kolejne kroki)
{ mik=aik/akk;
for(j=k+1; j<N; j++)
aij=aij-m.ik+akj ; }
wyklad:
Na współczesnych procesorach mamy dużą ilość pamięci wirtualnej - logicznej.
Page fault - strona niedostępna
Rys.
System typu SISD - sekwencyjny
Na wejściu mamy potok instrukcji (sekwencyjny), z jednego potoku robimy kilka. Dla jednego potoku wykonują się różne instrukcje równoległe.
Rys.
VLIM (Very Long Instruction Word) - nowa architektura procesorów : Itanium 64 - nowy procesor
Przykład: program niezoptymalizowany.
Założenia:
macierze o rozmiarze 1024×1024 - 1 mln słów
strona pamięci wirtualnej zawiera 65536 słów
jedna macierz wymaga 16 stron
dostępna pamięć RAM odpowiada 16 stronom - 1 mln słów
w przypadku sekwencyjnego dostępu do kolumn, oznacza to wystąpienie jednego „page fault” po każdych 64 kolumnach
Inner product approach -ijk
DO 30 I=1, N
DO 20 J=1,N
DO 10 K=1,N
C(I,J)=A(I,K)*B(K,J)+C(I,J)
10 CONTINUE
20 CONTINUE
30 CONTINUE
page faults: 1 mln*16=16 mln
I/O: 16 mln*0,5sek→około 93 dni
Dla jednego elementu C(I,J) trzeba mieć dostęp do całego wiersza macierzy A. Pamięć jest zapisywana według kolumn. Dlatego gdy odczytujemy nazwę kolumny aby otrzymywać kolejną pozycję wiersza i trzeba przeskoczyć przez 16 stron i dlatego mamy 16 mln błędów (to nie sa tak naprawdę błędy tylko momenty doładowania kolejnej strony z pamięci zew).
Program z zamienionymi pętlami:
Column- wise update of C - jik
DO 30 J=1, N
DO 20 K=1,N
DO 10 I=1,N
C(I,J)=A(I,K)*B(K,J)+C(I,J)
10 CONTINUE
20 CONTINUE
30 CONTINUE
macierz A: 1024*16 „page faults”
macierz B: 16 „page faults”
macierz C: 16 „page faults“
czas: 2,5 godziny
dwie wew pętle K,I obliczają wektor.
Algorytm blokowy:
Partitioning the matrices into block-columns - bloked jik
DO 40 J=1, N, NB
DO 30 K=1,N, NB
DO 20 JJ=J,J+NB-1
DO 10 KK=K,K+NB-1
C(:,JJ)=C(:,JJ)+A(:,KK)*B(KK,JJ)
10 CONTINUE
20 CONTINUE
30 CONTINUE
40 CONTINUE
macierze podzielone na bloki 256×256 tj. NB=256
macierz A: 4*16 „page faults”
macierz B: 16 „page faults”
macierz C: 16 „page faults“
razem 96 „page faults“→70 sek I/O
ATLAS (Automatically Tuned Linear Algebra Software)
Aby otrzymać blok macierzy C:
Mamy:
Program:
DO J=, N, NB
Bwork = ALPHA*B(:,J+NB-1)
DO I=1, M, NB
IF (PARTAL_MATRIX) Awork=A (I:I+NB-1,:)
Cwork(1:NB,1 :NB)=0
DO K=1, K ,NB
ON_CHIP_MATMUL(Awork,Bwork,Cwork)
END DO
C(I:I + NB -1,J:J +NB -1)=BETA*Cwork
END DO
END DO
Wykład
Odwzorowanie prac na procesory
Zbiór zadań (prac) T={t1...tn}.
Każde zadanie ma pracochłonność tiWi
Wi - złożoność, pracochłonność
Zadania trzeba przydzielić do czasu i przestrzeni do zbiorów procesorów.
P=(p1,p2...pm.) P- zbiór procesorów
Do każdego zadania trzeba przydzielić
ti -> {pi, i pi - procesor
i - moment rozpoczęcia tej pracy, bo zakładamy, że zadania są niepodzielne
szukamy sposobu optymalnego - musi być zadana funkcja celu
W sposób optymalny:
Dany: zbiór T, P zbiór procesorów
Znaleźć: uszeregowanie S - odwzorowanie zbiorów zadań F w zbór procesorów, czyli zbiór momentów czasowych
S:T -> P x (iloczyn kartezjański)
Minimalny czas realizacji algorytmu min
Dane: Zbiór T i maks. wartość . (czas realizacji algorytmu jest ograniczony)
Znaleźć: zbiór procesorów o minimalnym koszcie
Kolejna prace z listy prac przydzielamy do pierwszego wolnego procesora na liście
Nie istnieje algorytm optymalny w czasie będącego funkcją wielomianowej:
Nie ma czasu nx , jest czas xn
Przykład:
9 zadań
Ti, i=0, ... , 8
Wi= i * mod 3 +1
Uszeregować zbiór prac i procesorów i przydzielać kolejno listy prac do pierwszego wolnego procesora na lini.
P1 - 1 x
P2 - 2 x szybszy
P3 - 4 x szybszy
Praca - szeregujemy od najmniej złożonej do najbardziej złożonej:
W0 = 1 W1 = 2 W2 = 3 W3 = 1
W4 = 2 W5 = 3 W7 = 2 W8 = 3
Sortowanie topologiczne - tworzy się piętra
Algorytm listowy
Trzeba graf uporządkować za pomocą sortowania topologicznego.
1.Na górze te wierzchołki które nie zależą od żadnych innych
2. wierzchołki, które należą do tych, które są na 1 piętrze
3. zależą od 1 i 2,ale nie muszą od 2
4. zależą od 1,2,3 i nie muszą od 3...
wykład:
PROGRAMOWANIE WSPÓŁBIEŻNE:
PROCES-program sekwencyjny w trakcie wykonywania
DWA PROCESY WSPÓŁBIEŻNE-jeżeli jeden z nich rozpoczyna się przed zakończeniem drugiego.
Będą nas interesować jedynie takie procesy, których wykonania są od siebie uzależnione przy czym uzależnienie wynika z faktu, że
procesy są sobą WSPÓŁPRACUJĄ lub między sobą WSPÓŁZAWODNICZĄ.
KOMUNIKACJA I SYNCHRONIZACJA:
Współpraca wymaga od procesów komunikowania się. Akcje komunikujących się procesów muszą być częściowo uporządkowane w czasie, ponieważ informacja musi najpierw zostać utworzona zanim zostanie wykonana. Takie porządkowanie w czasie
różnych procesów nazywa się SYNCHRONIZACJĄ.
Współzawodnictwo także wymaga synchronizacji: - akcja procesu musi być wstrzymana jeżeli zasób potrzebny do jej wykonania jest w danej chwili zajęty przez inny proces.
PROGRAM WSPÓŁBIEŻNY jest zbiorem procesów (wątków)
PROBLEMY WZAJEMNEGO WYKLUCZANIA:- w teorii procesów współbieżnych wspólny obiekt, z którego może korzystać w sposób wyłączny wiele procesów np. (łazienka, koszyk w sklepie) nazywa się ZASOBEM DZIELONYM, natomiast fragment procesu, w którym korzysta on z obiektu dzielonego (mycie się, zakup) nazywa się SELEKCJĄ KRYTYCZNĄ.
-Problem wzajemnego wykluczania definiuje się następująco:
zsynchronizować N procesów, z których każdy w nieskończonej pętli na przemian zajmuje się WŁASNYMI SPRAWAMI i wykonuje sekcje krytyczną, w taki sposób, aby wykonanie sekcji krytycznych jakichkolwiek dwóch lub więcej procesów nie pokrywało się w czasie.
Aby ten problem rozwiązać, należy do treści tego procesu, wprowadzić dodatkowe instrukcje poprzedzające sekcję krytyczną (nazywa się PROTOKOŁEM WSTĘPNYM)
i instrukcje następują bezpośrednio po sekcji krytycznej (zwane PROTOKOŁEM KONCOWYM).
PRZYKŁAD PROBLEMY WZAJEMNEGO WYKLUCZANIA:
-MULTIPROCESOR czyli system równoległy z pamięcią wspólną
-dwa procesy współbieżne, z których jeden realizuje operacje x=x+1, a drugi x=x+2
-każda z powyższych operacji realizowana jest za pomocą trzech operacji maszynowych tj.(i)load x, (ii)add(1 lub 2), (iii)store x
przypuśćmy, że x=5, wówczas jeden z możliwych scenariuszy wygląda następująco:
1.Pierwszy proces pobiera swoja kopię x:x=5,
2.Pierwszy proces oblicza x=x+1 (lecz wartość, wynikowa nie zostaje jeszcze zapisana do pamięci wspólnej),
3.Drugi proces oblicza włącza się do akcji pobierając swoją kopię x:x=5,
4.Drugi proces oblicza x=x+2:x=7, nie zapisuje wyniku do pamięci wspólnej,
5.Pierwszy proces zapisuje swój wynik x=6 do pamięci,
6.Drugi proces zapisuje swój wynik x=7 do pamięci wspólnej.
Wniosek: otrzymujemy x=7 zamiast prawidłowego wyniku x=8.
Blokada i zagłodzenia
-w poprawnym programie współbieżnym tj. posiadającym własność żywotności, w każdym procesie powinno w końcu nastąpić oczekiwane zadanie.
-w niepoprawnym programie mogą wystąpić zjawiska blokady lub zagłodzenia
-zbiór procesów znajduje się w stanie blokady jeżeli każdy z tych procesów jest wstrzy-
mywany w oczekiwaniu na zdarzenie które może być spowodowane tylko przez jakiś inny proces z tego zbioru.
-inna nazwa zjawiska blokady to zastój, zakleszczenie lub martwy punkt
-specyficznym przypadkiem nieskończonego wstrzymywania procesu jest zjawisko zagłodzenia zwane także wykluczeniem
-jeżeli sygnał synchronizacyjny może być
odebrany tylko przez jeden z oczekujących nań procesów powstaje problem, który z procesów wybrać
Mechanizm synchronizacji
-nisko poziomowe: w jęz. niskiego poziomu÷przerywanie
-wysoko poziomowe: dostępne w jęz. wysokiego poziomu
Semafory
Semafor to abstrakcyjny typ danych, na którym oprócz określenia jego stanu początkowego można wykonywać tylko dwie operacje umożliwiające wstrzymywanie procesów a mianowicie:
-opuszczanie semafora
-podniesienie semafora
o których zakłada się, że są niepodzielne, co
oznacza, że w danej chwili może być wykonywana tylko jedna z nich.
Semafor binarny
Def. Klasyczna
-opuszczenie semafora binarnego to wykonanie instrukcji PB(S):
czekaj aż s==1; s=0
-podniesienie semafora binarnego VB(S):
s=1
Def. Praktyczna:
-opuszczenie semafora binarnego PB(S):
jeżeli s==1, to s=0, w przeciwnym razie wstrzymaj działanie procesu wykonującego tę operację
-podniesienie semafora binarnego VB(S):
jeżeli są procesy wstrzymane w wyniku wykonania operacji opuszczenia semafora s to wznów jeden z nich,w przeciwnym razie s=1
Semafor ogólny:
Def. Praktyczna - opószczeniue semafora ogólnego P(S): jeżeli S>0 to S=S-1, w przeciwnym razie wstrzymaj działanie procesu wykonującego tą operację; Podniesienie semafora binarnego V(S): jeżeli są procesy wstrzymane w wyniku wykonania operacji opuszczania semafora S, to zwarty jeden z nich, w przeciwnym razie S=S+1
Definiowanie zmiennych semaforowych w programach.
Semafor ogólny: semaphore sem=4;
Semafor binarny: binary semaphore=1;
Przykłady programów współbieżnych z wykorzystaniem semaforów:
Wzajemne wykluczenia:
Int n=1;
Binary semaphore s=1;
Proces P(int i);
{while {true}
{własne sprawy;
PB(s);
Sekcja krytyczna;
VB(s);
}
} Problem pięciu filozofów.
Rozwiązanie z możliwością blokady
Binary semaphore widelec[5]={1,1,1,1,1};
Proces filozof(int i)
{while {true}
{PB(widelec[i]);
PB(widelec[(i+1)%5]);
Jedzenie;
VB(widelec[i]);
VB(widelec[i+1)%5]);
}
}
Rozwiązanie porawne:
Binary semaphore widelec[5]={1,1,1,1,1};
Semaphore lokaj=4;
Proces filozof(int i)
{while {true}
{myślenie;
P(lokaj);
PB(widelec[i];
PB(widelec[(i+1)%5]);
Jedzenie;
VB(widelec[i]);
VB(widelec[(i+1)%5]);
V(lokaj);
}
}
C
M
Potokowość
Potok2
Potok1
C32
N
K
B23
B22
B12
A31
M
A
A32
A33
K
B
N
×
Wyszukiwarka
Podobne podstrony:
wyklady-pwir, Studia, 6. Semestr, Przetwazanie wspolbiezne
wyklady-pwir, Studia, 6. Semestr, Przetwazanie wspolbiezne
ZZL-wyklady, Materiały STUDIA, Semestr III, Zarządzanie zasobami ludzkimi, ZZL
KIEROWANIE PROCESAMI INWESTYCYJNYMI - Notatki z wykładów - WODZU, STUDIA, semestr 5, Kierowanie Proc
wyklady 2czesc, studia, 3 semestr, Programowanie
Marketing (wykład ostatni), studia, semestr 3, marketing
SMiPE - Kolokwium wykład ściąga 1, STUDIA, SEMESTR IV, Statystyka matematyczna i planowanie eksperym
zarzadzanie wyklad, Edukacja, studia, Semestr VIII, Zarządzanie, zarzadzanie
Hodowle komórek i tkanek zwierzęcych wykład 1 konspekt, Studia, I semestr III rok, Praktikum z hodow
Socjologia wychowania - wyklady.x, Pedagogika - studia, I semestr - ogólna, Socjologia wychowania
psycho wykłady (1), Materiały STUDIA, Semestr VII, Psychologia zarządzania
SMiPE - Kolokwium wykład ściąga 2, STUDIA, SEMESTR IV, Statystyka matematyczna i planowanie eksperym
wyklady z kartografii2, Studia, 5 semestr, kartografia, egzamin
Wykład IVPNOM, STUDIA, SEMESTR I, PNOM
Wyklad 1 z enzymologii, Studia, Przetwórstwo mięsa - Semestr 1, Enzymologia, Wykłady
wykłady drób - 28.03.2010, Studia - materiały, semestr 6, Przetwórstwo mięsa drobiowego, wykłady
Ostatni wykład 28, Studia, Przetwórstwo mięsa - Semestr 1, mgr, I rok, higiena mięsa i przetworów mi
temp krytyczna, TRANSPORT PWR, STUDIA, SEMESTR II, FIZYKA, fizyka-wyklad, zagadnienia opracowane, za
więcej podobnych podstron