KLASYCZNA ANALIZA CZYNNIKOWA

• analiza czynnikowa jest metodą badania struktury wewnętrznych zależności obserwacji wielowymiarowych

• każda zmienna obserwowalna (wejściowa) przedstawiana jest jako kombinacja liniowa pewnej liczby nieobserwowalnych zmiennych, zwanych czynnikami, wspólnych dla całego zbioru zmiennych wejściowych oraz jednego nieobserwowalnego czynnika swoistego dla tej zmiennej

• czynniki wspólne i czynniki swoiste nie są ze sobą skorelowane.

• celem analizy czynnikowej jest znalezienie takiego zbioru czynników wspólnych oraz określenie ich relacji ze zmiennymi obserwowalnymi, który pozwala na wyjaśnienie struktury powiązań między zmiennymi obserwowalnymi

ALGORYTM ANALIZY CZYNNIKOWEJ

• budowa macierzy danych wejściowych o postaci:

, i=1,2,...,n; j=1,2,...m, (6.0)

gdzie:

x_ij - wartość j-tej zmiennej w i-tym obiekcie. Zakładamy przy tym, że zmienne wejściowe mają rozkład normalny.

• przedstawienie wystandaryzowanych zmiennych wejściowych jako kombinacji linowej czynników:

, (6.1)

gdzie:

- wystandaryzowana macierz obserwacji (m xn), przy czym zji jest wartością wystandaryzoanej j-tej zmiennej w i-tym obiekcie,

- macierz ładunków czynnikowych czynników wspólnych (n x s), przy czym w_jl jest ładunkiem czynnikowym znajdującym się przy j-tej zmiennej i l-tym czynniku wspólnym,

- macierz czynników wspólnych (s x n), przy czym f_li jest wartością l-tego czynnika wspólnego w i-tym obiekcie,

- macierz diagonalna ładunków czynnikowych czynników swoistych (n x m), przy czym b_j jest ładunkiem czynnikowym j-tego czynnika swoistego,

- macierz czynników swoistych (n x m), przy czym u_ij jest wartością j-tego czynnika swoistego w i-tym obiekcie.

• zakłada się, że wariancję (zasób informacyjny) każdej ze zmiennej wejściowej można rozłożyć na wariancję wyjaśnianą przez czynniki wspólne (zasoby informacyjne danej zmiennej wejściowej wspólne z zasobami informacyjnymi innych zmiennych wejściowych) oraz przez czynnik swoisty (zasoby informacyjne tej zmiennej wejściowej nie powielane przez inne zmienne wejściowe):

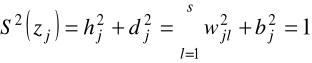
, j=1,2,...,m (6.2)

gdzie:

- zasoby zmienności wspólnej j-tej zmiennej,

- zasoby zmienności swoistej j-tej zmiennej.

• szacunek zasobów zmienności wspólnej

• dążymy do eliminacji wpływu czynników swoistych na rzecz czynników wspólnych, co jest równoważne z minimalizacją wpływu na kształtowanie się wartości zmiennych wejściowych wszystkich innych zmiennych poza czynnikami wspólnymi

• eliminacja tego wpływu odbywa się poprzez zastąpienie w macierzy korelacji R współczynników korelacji znajdujących się na głównej przekątnej (współczynników korelacji, których wartości są równe 1), zasobami zmienności wspólnej (wartościami najczęściej mniejszymi od 1), uzyskując w ten sposób tzw. zredukowaną macierz korelacji o postaci:

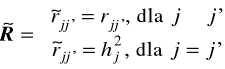
, j,j'=1,2,...,m, (6.3)

• zasoby zmienności wspólnej szacowane są najczęściej za pomocą formuł:

⇒ średnia arytmetyczna współczynników korelacji danej zmiennej z innymi zmiennymi:

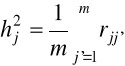
, j,j'=1,2,...,m; j≠j', (6.4)

⇒ maksymalna wartość bezwzględna z współczynników korelacji danej zmiennej z innymi zmiennymi:

, j,j'; j,j'=1,2,...,m; j≠j', (6.5)

⇒ współczynnik determinacji wielorakiej danej zmiennej z innymi zmiennymi:

, j=1,2,...,m, (6.6)

gdzie:

x'=[x_j'], j'=1,2,...,m; j≠j', (6.7)

⇒ formuła triad:

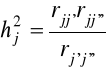
, j,j',j”=1,2,...,m; j≠j'≠j'', (6.8)

gdzie:

- najwyższe wartości współczynników korelacji j-tej zmiennej z innymi zmiennymi.

METODY SZACUNKU ŁADUNKÓW CZYNNIKOWYCH

METODA OSI GŁÓWNYCH

• metoda osi głównych jest stosowana przy wyznaczaniu współczynników głównych składowych

• jedyną różnicą, w stosunku do procedury stosowanej w analizie głównych składowych, jest tutaj operowanie w miejsce pełnej macierzy korelacji zredukowaną macierzą korelacji, w której na głównej przekątnej zamiast jedynek znajdują się wartości zasobów zmienności wspólnej kolejnych zmiennych wejściowych

METODA CENTROIDALNA

Ogólna charakterystyka

• metoda centroidalna opiera się ona na geometrycznym podejściu do analizy czynnikowej

• kolumny macierzy danych wejściowych można interpretować w ujęciu geometrycznym jako konfigurację m wektorów zmiennych w n wymiarowej przestrzeni euklidesowej Rⁿ. Wzajemny układ wektorów, reprezentujących zmienne, określa korelacje pomiędzy zmiennymi, tzn. cosinusy kątów między wektorami są równe współczynnikom korelacji pomiędzy zmiennymi

• zakłada się, że osie poszczególnych czynników przechodzą przez środki ciężkości (centroidy) konfiguracji wektorów

• sposób wyznaczania osi czynnikowych jest tutaj podobny jak w metodzie osi głównych, a mianowicie kolejne czynniki wyjaśniają maksymalną część zmienności wspólnej zmiennych wejściowych, z tym, że czynniki są wyodrębniane w inny sposób

• wartości ładunków czynnikowych stanowią współrzędne punktów reprezentujących zmienne w nowym, ortogonalnym układzie odniesienia

Algorytm metody

• w pierwszym kroku szukane są ładunki czynnikowe pierwszego czynnika, którego udział w wyjaśnianiu zasobów wspólnych zmienności jest największy

• od strony geometrycznej oznacza to, że oś czynnikowa pierwszego czynnika przechodzi przez środek ciężkości punktów reprezentujących zmienne

• ładunki pierwszego czynnika obliczamy w oparciu o wzór:

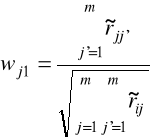
, j=1,2,...,m. (6.11)

• po wyznaczeniu ładunków pierwszego czynnika tworzymy, podobnie jak w metodzie głównych składowych, macierz pozostałości korelacyjnych, która stanowi podstawę wyznaczania ładunków czynnikowych drugiego z czynników

• w uzyskanej macierzy pozostałości korelacyjnych sumy jej elementów po wierszach i po kolumnach są równe zeru co uniemożliwia bezpośrednie obliczenie ładunków czynnikowych

• odwracamy znaki algebraiczne w wybranej kolumnie i wierszu macierzy

• zmiany znaków dokonujemy w kolejnych wierszach i kolumnach aż do uzyskania najmniejszej liczby znaków ujemnych w całej macierzy pozostałości korelacyjnych

• na głównej przekątnej umieszczamy ponownie wyznaczone zasoby zmienności wspólnej

• obliczamy ładunki czynnikowe drugiego czynnika

• przywracamy pierwotne znaki tych zmiennych, dla których wcześniej zostały dokonane zmiany znaków

• obliczamy ładunki czynnikowe kolejnych czynników w analogiczny sposób

METODA NAJWIĘKSZEJ WIARYGODNOŚCI

Ogólna charakterystyka

• zakładamy na wstępie liczbę czynników wspólnych, którą chcemy uzyskać

• przyjmujemy, że dane wejściowe pochodzą z próby o wielowymiarowym rozkładzie normalnym

Algorytm metody

• ładunki czynnikowe wyznaczane są w taki sposób aby zmaksymalizować prawdopodobieństwo wyjaśniania przez model współczynników korelacji w wejściowej, obserwowalnej macierzy korelacji

• ładunki czynnikowe są szacowane, podobnie jak w metodzie osi głównych, poprzez rozwiązanie równania charakterystycznego o postaci:

, (6.12)

gdzie
jest definiowana jako:

(6.13)

przy czym:

U² - macierz wariancji czynników specyficznych szacowana w kolejnych iteracjach.

• wariancja specyficzna traktowana jest tutaj jako wariancja błędu, który minimalizujemy maksymalizując jednocześnie odtworzenie elementów wejściowej macierzy korelacji przez szacowane ładunki czynnikowe

• we wstępnej iteracji, szacując macierz zredukowaną
  , stosujemy metodę osi głównych

METODY ROTACJI CZYNNIKÓW

Ogólna charakterystyka

• uzyskany, w wyniku stosowania różnych metod szacunku ładunków czynnikowych, zbiór czynników nie jest jedynym możliwym układem czynnikowym przy ustalonej wcześniej wielkości zasobów zmienności wspólnej

• tą samą zredukowaną macierz korelacji możemy odtworzyć za pomocą nieskończenie wielu różnych macierzy ładunków czynnikowych otrzymanych w wyniku obrotu (rotacji) układu osi czynnikowych dookoła swojego początku, przy czym udział czynników w wyjaśnianiu wspólnej wariancji (suma ich zasobów informacyjnych) nie ulega w wyniku rotacji zmianie

• podstawowym celem rotacji układu osi czynnikowych jest uzyskanie jak najprostszej interpretacji poszczególnych czynników, czyli tzw. prostej struktury ładunków czynnikowych

• prowadzą one do wyodrębnienia rozłącznych grup zmiennych wejściowych, z których każda zawiera zmienne o wysokich ładunkach dla jednego czynnika, średnie dla kilku innych czynników oraz bliskie zeru dla pozostałych czynników

• możemy wyróżnić dwie grupy metod rotacji czynników, a mianowicie rotacje ortogonalne oraz rotacje ukośne

ROTACJE ORTOGONALNE

Ogólna charakterystyka

• metody rotacji ortogonalnych polegają na poszukiwaniu ortogonalnej macierzy transformacji spełniającej warunek:

, (6.16)

gdzie:

B=[b_jl] - macierz ładunków czynnikowych (m x s) po rotacji osi czynnikowych,

T=[t_ll'] - macierz transformacji (s x s).

• elementy macierzy transformacji określają wielkość kątów, o jakie należy obrócić układ osi czynnikowych

• zasoby zmienności wspólnej poszczególnych zmiennych wejściowych nie ulegają zmianie, czyli zachodzi następująca zależność:

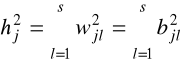
, j=1,2,...,l (6.17)

• zachodzi również równość o postaci:

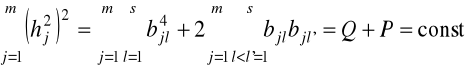
, (6.18)

określona jako niezmiennik transformacji ortogonalnej.

• powyższa równość wskazuje, że maksymalizacja jednego z jej składników prowadzi do minimalizacji drugiego składnika

Kryterium quartimax

• przeprowadzamy rotację osi czynnikowych minimalizując wartość składnika P i jednocześnie maksymalizując składnik Q, czyli dążymy do prostej struktury maksymalizując wariancję kwadratów ładunków czynnikowych dla każdej zmiennej:

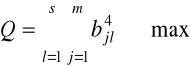
(6.19)

• metoda ta prowadzi do maksymalizacji wartości dużych ładunków czynnikowych oraz minimalizacji małych ładunków czynnikowych

• przedstawione kryterium quartimax nazywane jest surowym, gdyż nadaje większą wagę zmiennym mającym większy udział w zasobach zmienności wspólnej

Kryterium varimax

• miarą prostoty danego czynnika jest wyrażenie o postaci:

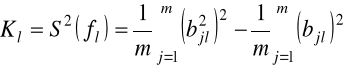
, l=1,2,...s. (6.20)

• dany czynnik odznacza się największą interpretowalnością (prostotą) gdy powyższe wyrażenie (wariancja kwadratów ładunków czynnikowych l-tego czynnika) przyjmuje wartość maksymalną, co odpowiada sytuacji, że jego ładunki czynnikowe dla zmiennych wejściowych albo dążą do jedności, albo do zera

• rotacja osi czynnikowych, prowadząca do prostej struktury czynnikowej, jest tak dokonywana aby zmaksymalizować sumę wariancji kwadratów ładunków czynnikowych wszystkich czynników:

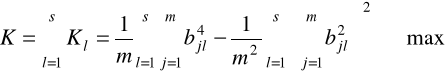
(6.21)

Kryterium znormalizowane

quartimax oraz varimax

• normalizacja ładunków czynnikowych prowadzi do neutralizacji większego wpływu na uzyskiwane rozwiązania czynników początkowych o dużych wartościach

• normalizacja przebiega według formuły:

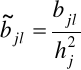
, j=1,2,...m; l=1,2,...s. (6.22)

• kryterium znormalizowanego quartimax przyjmuje postać:

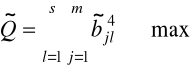
(6.23)

• kryterium znormalizowanego varimax przybiera postać:

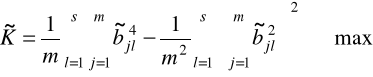
(6.24)

• od strony technicznej kryterium quartimax koncentruje się na upraszczaniu wierszy macierzy ładunków czynnikowych, a kryterium varimax na upraszczaniu kolumn tej macierzy

Kryteria biquartimax i equamax

• kryteria biquartimax i equamax łączą odpowiednio ważone warunki quartimax i varimax, co możemy zapisać:

, (6.25)

gdzie: α,β - wagi.

• po przemnożeniu przez liczbę zmiennych m kryterium to przyjmuje ogólną postać:

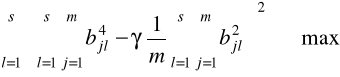
, (6.26)

gdzie: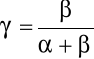
.

• przy przyjęciu wag jednostkowych dla obu kryteriów, tzn. dla γ=0,5, otrzymujemy surowe kryterium biquartimax o postaci:

(6.27)

• wersja znormalizowana kryterium biquartimax może być przedstawiona następująco:

(6.28)

• przy przyjęciu przyjmiemy, że waga dla surowego kryterium quartimax jest jednostkowa, a waga dla surowego kryterium varimax równa jest połowie liczby czynników, tzn. dla
  , equamax ma postać:

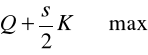
(6.29)

• znormalizowane kryterium equamax zapisujemy jako:

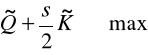
(6.30)

OKREŚLANIE LICZBY CZYNNIKÓW

• weryfikujemy hipotezę, że przy przyjętej liczbie czynników zaproponowany przez nas model wystarczająco dokładnie odtwarza współczynniki korelacji między zmiennymi wejściowymi

• wykorzystujemy w tym celu statystykę chi-kwadrat o postaci:

, (6.36)

gdzie:

S - macierz kowariancji pomiędzy zmiennymi wejściowymi,

,

o liczbie stopni swobody równej:

.

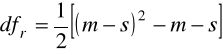
• weryfikacja odpowiedniej hipotezy odbywa się w sposób interacyjny począwszy od modelu z jednym czynnikiem

• w przypadku nieadekwatywności tego modelu zwiększamy liczbę czynników o 1

Charakterystyka cząstkowych technik analizy czynnikowej

		Obrazy
Struktura danych	Element stały	punktów	wymiarów	Technika analizy czynniko-wej	Podstawa obliczeń	Cel analizy czynnikowej
Obiekty x cechy X(n, m)	okres	obiekty	cechy	R	macierz korelacji cech na podstawie szeregów przekrojowych R(m, m)	redukcja zbioru cech
Cechy x obiekty X(m, n)	okres	cechy	obiekty	Q	macierz podobieństwa obiektów P(n, n)	typologia obiektów o podobnych relacjach wartości cech
Okresy x cechy X(k, m)	obiekt	okresy	cechy	P	macierz korelacji cech na podstawie szeregów czasowych R(m, m)	redukcja zbioru cech

Cechy x okresy X(m, k)	obiekt	cechy	okresy	O	macierz podobieństwa okresów P(k, k)	typologia okresów o podobnych relacjach wartości cech (periodyzacja)
Obiekty x okresy X(n, k)	cecha	obiekty	okresy	T	macierz korelacji okresów na podstawie szeregów przekrojowych R(k, k)	ustalenie istotnych okresów
Okresy x obiekty X(k, n)	cecha	okresy	obiekty	S	macierz korelacji obiektów na podstawie szeregów czasowych R(n, n)	typologia obiektów o podobnych zmiennych w czasie według danej cechy

CHARAKTERYSTYKA ZŁOŻONYCH TECHNIK

ANALIZY CZYNNIKOWEJ

Struktura danych	Obrazy		Podstawa obliczeń	Cel analizy czynnikowej	Technika
		punktów				wymiarów
Obiekty ⋅ cechookresy X(n, mk)	obiekty	cechy w różnych okresach	mierniki korelacji cech i okresów na podstawie szeregów przekro-jowych R(mk, mk)	jednoczesna redukcja cech i okresów	RT
Cechookresy ⋅ obiekty X(mk, n)	cechy w różnych okresach	obiekty	macierz podobieństwa obiektów P(n, n)	typologia obiektów według podobieństwa cech w różnych okresach	QS
Okresy ⋅ cechoobiekty X(k, nm)	okresy	cechy w różnych okresach	macierz korelacji cech i obiektów na podstawie szeregów czasowych R(nm, nm)	redukcja cech wraz z typologią okresów	PS
Cechoobiekty ⋅ okresy X(nk, m)	cechy w różnych okresach	okresy	macierz podobieństwa okresów P(k, k)	typologia okresów o podobnych relacjach wartości cech w różnych okresach	OT
Obiektookresy ⋅ cechy X(m, nk)	cechy w różnych okresach	cechy	macierz korelacji cech na podstawie szeregów przekrojowo-czasowych R(m, m)	redukacja cech	RP
Cechy ⋅ obiektookresy X(m, nk)	cechy	cechy w różnych okresach	Macierz podobieństwa obiektów i okresów P(nk, nk)	typologia obiektów i okresów (periodyzacja łączna)	QO